Roboartist is a 4 stage robotic arm that can sketch out the outline of any image using a pen/pencil on an A3 sheet using Edgestract, our custom made edge detection algorithm. The project relies on the core engine to extract the edge from the image uploaded for processing. An Arduino Mega controls the servos using information sent from MATLAB (Fret not, a more open implementation is on the way) via the USB/Bluetooth port.
THE HARDWARE
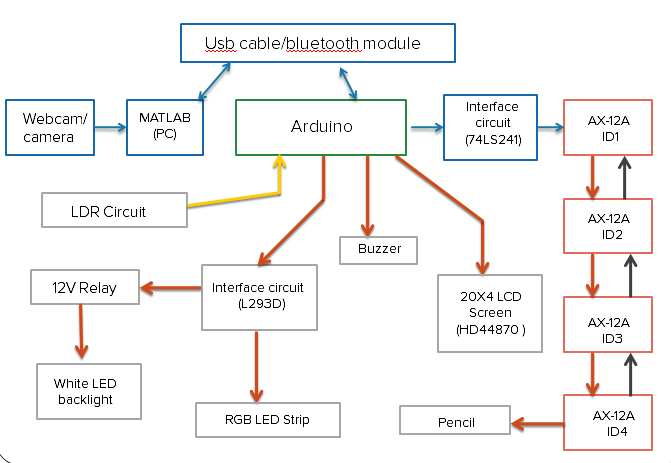
The basic layout of the hardware is as above. Image acquisition is achieved through a Webcam or a camera. We've also allowed scanning of existing JPEGs. Although an RGB LED strip and an LCD Screen weren't strictly necessary, we threw it in just for fun. What does really improve the product design is the white LED backlight constructed from LED strips. The light diffuses through the paper, providing a nice aura to the performances of the Roboartist.
THE SOFTWARE
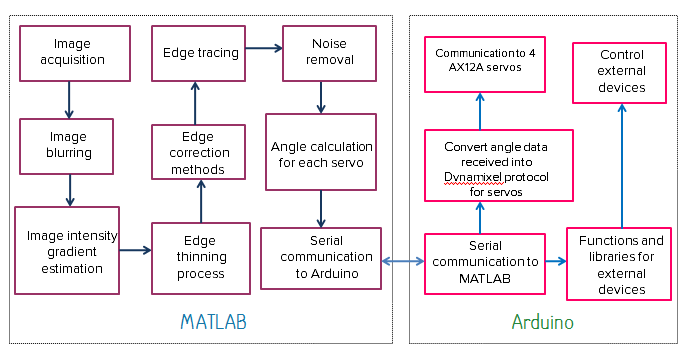
Here's how the software is structured. The basic idea is to let MATLAB do all the heavy lifting and let Arduino focus on wielding the pencil. The program requires the user to control a few parameters to eek out the noise and obtain a good edge output. Once finished the program communicates with the Arduino (via Bluetooth, 'cos too many wires are not cool!).
STAGES
Here is a quick peek at the image processing stages involved:

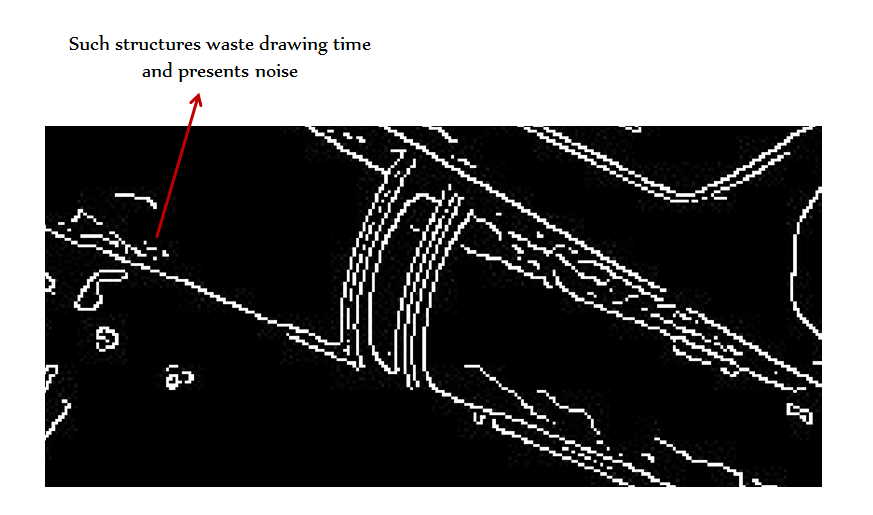
Each slice is from a consecutive series of DIP stage. We've been using the Canny edge detection algorithm initially, but we've now built and switched to Edgestract, a more optimized algorithm for drawing. We have been running the algorithm over various types of images and logging the results.
We'll tell you more in the coming updates.
 niazangels
niazangels
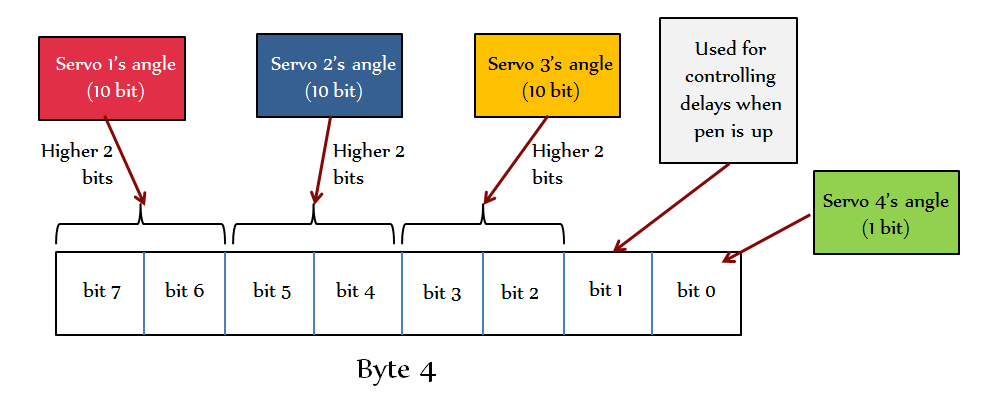











 Rudolph
Rudolph

 Stryker295
Stryker295
 Mister Malware
Mister Malware
How much did this project cost to u ? Thanks