Introduction
The identification of the system parameters from a real dynamical system is often required for model control or simulations. In many cases the dynamical system is a PT2 system with the transfer function H(s).
In case of D<1 the system is underdamped and there exists a simple way to extract the parameters k, D and wn from the step-response of the system (see PT2-System Wikipedia (german)).
In case of D>1 up to now i do not have found any simple solution to do that job and this article describes a simple method to determine the two time constans T1 and T2 of the transfer function
Method to get T1 and T2 with the measured step-response
1. Capture the step-response y(t) and normalize it
Capture the step-response y(t) and normalize so that you get the step-response with an unit-step input signal (step from 0 to 1).
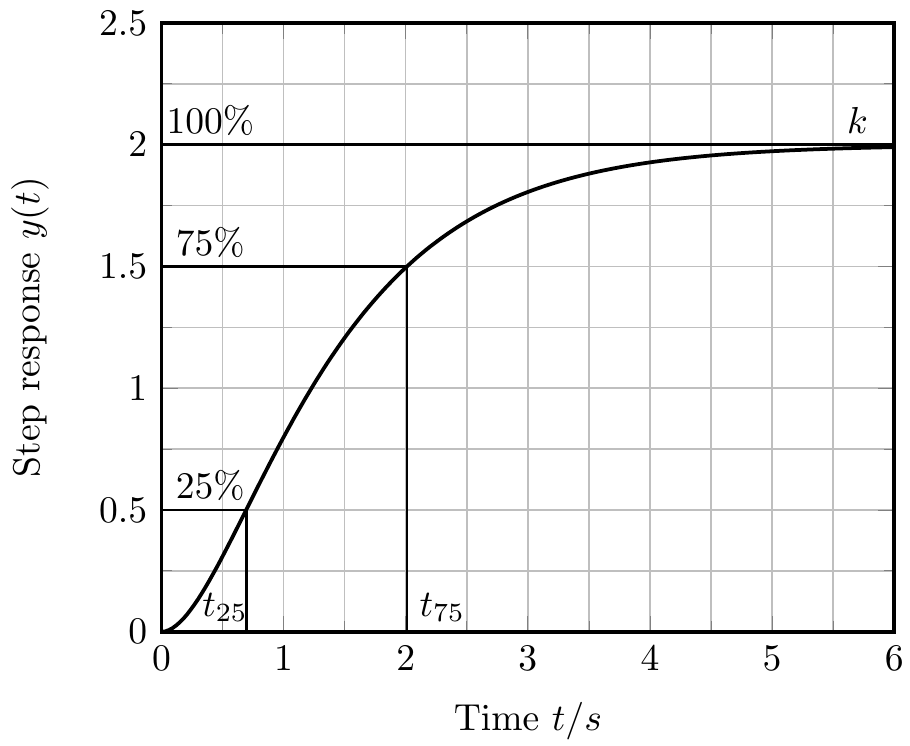
2. Determine steady-state gain k
You can measure the gain k in steady-state (in the example above k=2).
3. Measure t25 and t75
Measure the timestamps where the step-response y(t) reaches 25% and 75% of the steady-state value.
4. Calculate the time-constants T1 and T2
Now calculate the time-constants of the transfer function H(s) with the following method
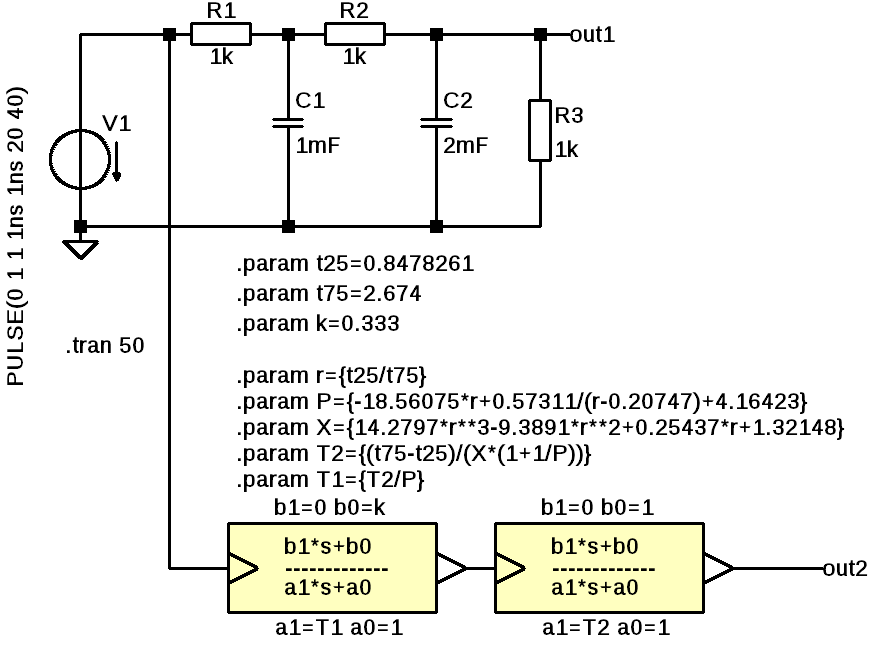
Example with ltSpice
Following example demonstrates the functionality of this approach. The step-response of a passive RC filter of 2nd order was simulated, k, t25 and t75 measured with the cursors, then T1 und T2 were calculated using ltSpice parameters and then the step-response of the analog circuit was compared with the identified transfer function H(s).
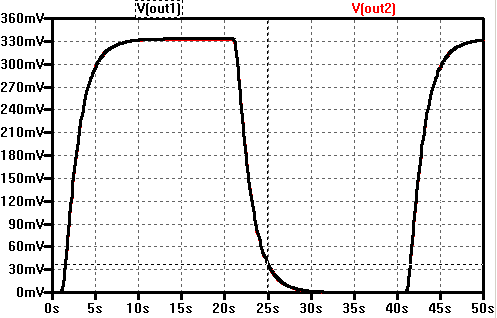
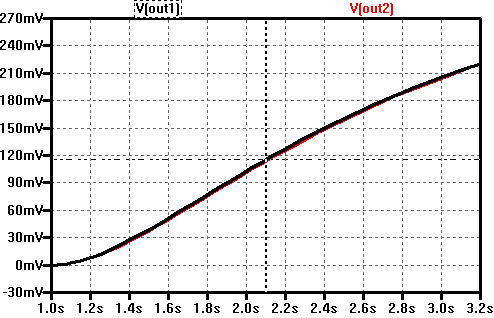
Conclusion
Many times i identified T1 and T2 of overdamped PT2 systems by fast try and error or some numerical methods. But the results were bad or it was a huge effort to get good results.
The method presented in this article allows now to determine transfer function with two simple measurements and returns the both time-constants with a high accuracy.
Feel free to test this method and give me some feedback of your experience.
I used the computer algebra system maxima to do the derivation of this equations with numerical methods (not analytical).
 weingaunity
weingaunity
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
OK, that makes more sense. Nice explanation. I can recommend two books that might have this topic. A book by Dorsey, "Continuous and Discrete Control Systems" and the book by Daniel Graupe, "Identification of Systems". You might find them in PDF here: http://gen.lib.rus.ec/
Regards,
Jose
Are you sure? yes | no
I didn't understand in step 1 why you normalize the step response? Do you mean setting u(t)=1 and obtaining y(t)? Or do you mean setting y(t) = y(t)/ymax, where ymax is the maximum value of y(t). In the latter case k = 1. Which case do you mean?
Thanks.
Are you sure? yes | no
Yes, i mean to normalize to input u(t)=1
u(t)=u_measured(t)/umax
y(t)=y_measured(t)/umax
Give me some feedback about this method when you used it for an example.
Are you sure? yes | no