[Hello future reader. This article refers to OpenSCAD 2018.05.05, please check if it still applies later on]
3D printing internal and external threads is interesting for many reasons.
Unlike gears that invariably wear rapidly and cannot measure up compared to cast or subtractively machined parts, they are pretty functional and allow the common maker to interface with custom and standardized bolts, pipes, valves, soda bottles and canisters - and that's on top of the liberty to create your own threaded mating components within the confines of your design.
The generalized approach presented here supports arbitrary thread geometries and numbers of starts.
Shown below are single start inside and outside threads as well as a swivel nut with a "faster" 3-start thread, all modelled to match commercial water bottles - the small one is "PCO-1881" known from 1.5L soda bottles, the larger one is "48-41" for 3-5L jugs:

Only right-hand threads are supported but left-handed threads are easy to get by applying mirror([0,1,0]) to the output. That's the OpenSCAD way :)
While the core idea of a straight thread - the helical profile wrapped onto a cylinder - is rather straight forward, generating nice geometry that does not disintegrate along the way from model rendering thru .stl export to the slicer tool deserves a little bit of attention.
What do I mean by "nice geometry"?
- "embossed threads" on a curved surface or
- manifold additive threads (demonstrated here, imho more universal)
- regular mesh / regular connectivity of trangles / quadrilaterals (no crazy pointy aspect ratios and cell size changes)
- low polygon count and accurate / efficient reproduction of the thread profile
- geometry matched to the rest of the model
in short, what we don't want is unnecessary structure, gaps, holes and mismatch of resolution of the threads and the rest of the geometry.
What I'm going to walk you through here is a way to create helical thread forms just like the ones you'd strip when overtightening a bolt:

http://www.tribology-abc.com/calculators/e3_6f.htm
Since OpenSCAD is am open source work in progress, users do not necessarily work with a version that has the latest features, documentation may not be up to date and forum posts claiming "it cannot be done" are repeatedly being invalidated by software revisions, adding to the confusion.
Let's go over what doesn't work (hopefully gaining some insights), then look at my proposed approach. If you just want the answers, please scroll down :)
linear_extrude()
As an example: without an operator that creates dedicated helical structures people are using linear_extrude() with twist to get something helical:

The problem here is that like fanning a deck of cards you'll end up with tucked-in faces and serrated outsides - as seen on Thingiverse:

And here's another one with a bit of discussion from 2014:
https://www.thingiverse.com/thing:368073/#comments
rotate_extrude()
Unfortunately as of now rotate_extrude() which should be closer to creating helical objects has learned partial rotations (not supported in 2015 builds for Windows) but cannot create helical extrusions. There's also no special treatment for the ends.
One could create a 180° arc and mirror it but as soon as these arcs are tilted to follow the helical pattern, the end faces where two arcs butt to form a full turn rotate in opposite directions. You can partition the arcs to your heart's content, this problem will never vanish:

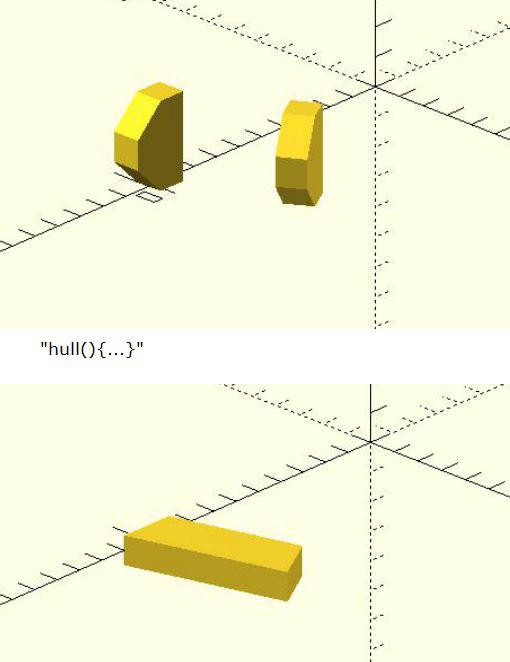
hull()
The obvious way to get the end face of an arc segment and the starting face of the following segment to stay aligned is to start with them by definition and then wrap the space in between with hulls. I gave up at the point where some geometry seemed to be "simplified" into a brick. This behavior may change with upcoming revisions but there are better methods to begin with.
Ok, then how to?
Prerequisites:
Now we're basically down to creating geometry from a list of vertices and triangles, having full control over how the surface mesh turns out. Luckily there are two sets of libraries to help us out.
Starting with a recent development snapshot for your platform of choice:
OpenSCAD http://www.openscad.org/downloads.html
and additionally
scad-utils https://github.com/openscad/scad-utils
list-comprehension https://github.com/openscad/list-comprehension-demos
under Windows, the libraries have to be cloned/copied into your <user>\Documents\OpenSCAD\libraries folder.
As of this writing there's also a pending modification to skin.scad to make the fancy toroidal geometry part of the example work, see
https://github.com/openscad/list-comprehension-demos/issues/8
but this is disconnected from the initial effort of creating nice threads.
Download:
For now I put up thread_profile.scad on github. If you've created new thread profile definitions I'd be happy to add them to the library. Just drop me a message.
https://github.com/MisterHW/IoP-satellite/tree/master/OpenSCAD%20bottle%20threads
The Approach:
With that out of the way, what is being shown is the generation of a helically arranged 1-dimensional array of vertical polygon() sections wrapped in a skin() made of triangles, the latter being an extension to polyhedron(). This thread helix can then be merged with the rest of the geometry via the boolean union() operator.

A radial function is introduced to create tapered ends, the Higbee cut. This is done to let the the threads start / end with a fully formed profile, avoiding galling.
Adding a cylinder and lead-in / lead-out taper this then becomes:

How to create new thread profiles:
First you'll need exact thread dimensions, e.g. obtained with a caliper or by gluing a sacraficial neck and cap piece together, cutting it in half and sticking the sanded cross section in a flatbed scanner (along with horizontal and vertical reference objects for scale) or even an official dimenional drawing like this one:
If for a neck finish the cap profile is missing, its complementary profile has to be inferred, including some proper clearances. There's also a bit of leeway for shaping the non-load-bearing side of the thread profiles.
Let's go over the code.
As per https://en.wikibooks.org/wiki/OpenSCAD_User_Manual/The_OpenSCAD_Language#Special_variables_2
which don't seem to work across files it seems function declarations are a generalized way to export constants and lists from libraries, so I'm using the function construct to create parameter sets for individual thread profiles to be fed to the generating module straight_thread(...).
// PCO-1881 soda bottle neck thread
function bottle_pco1881_neck_clear_dia() = 21.74;
function bottle_pco1881_neck_thread_dia() = 24.94;
function bottle_pco1881_neck_thread_pitch() = 2.7;
function bottle_pco1881_neck_thread_height() = 1.15;
function bottle_pco1881_neck_thread_profile() = [
[0, 0],
[0, 1.42],
[bottle_pco1881_neck_thread_height(), 1.22],
[bottle_pco1881_neck_thread_height(), 0.22]
];
Note the 2D thread profile is defined such that x == 0 is at the minor (major) diameter of the outside (inside) thread because for additive thread forms that's the outside (inside) cylindrical reference surface.
Next, we'll look at how module straight_thread() generates the 3D shape:
// helical thread with higbee cut at start and end
// to be attached to a cylindrical surface with matching $fn
module straight_thread(section_profile, pitch = 4, turns = 3, r=10, higbee_arc=45, fn=120)
{
$fn = fn;
steps = turns*$fn;
thing = [ for (i=[0:steps])
transform(
rotation([0, 0, 360*i/$fn - 90])*
translation([0, r, pitch*i/$fn])*
rotation([90,0,0])*
rotation([0,90,0])*
scaling([0.01+0.99*
lilo_taper(i/turns,steps/turns,(higbee_arc/360)/turns),1,1]),
section_profile
)
];
skin(thing);
}
In short, a 2D thread profile is passed as section_profile and in a for loop, turns*$fn copies are positioned in 3D space to then be enveloped with a polygonal skin().
The chain of transformation operations create uniaxial scaling, rotate the 2D shape out of its construction plane, translate it to the start of the helix and then parametrically rotate-translate it along the helical path.
The axes of rotations and the order in which they are applied has been determined so that the section is tilted upright and positioned in a way that matches how cylinder() creates faces, the alignment becomes obvious at small facet counts $fn.
In subtractive machining terms, a Higbee cut removes partially formed thread which would otherwise create a ramp of knife edge that could cut into the mating thread at an angle, destroying both sides. It also defines a nice ramp that makes the pieces click as you rotate a loose lid that "falls back down" one turn.
Here, a uniaxial scaling operation affecting the start and end cross sections is applied to the 2D profile. Alternatively, the thread profile would start and end abruptly, creating a stress riser and sharp corners undesirable in FDM printing, or worse one would intersect the thread profile with an inside cone and again end up with partial threads.
// radial scaling function for tapered lead-in and lead-out
function lilo_taper(x,N,tapered_fraction) = min( min( 1, (1.0/tapered_fraction)*(x/N) ), (1/tapered_fraction)*(1-x/N) )
;
Side note: scaling the thread profile down to zero is not permitted per se because it would need special treatment for non-regulatities such as zero-area polygons or just a change in connectivity (all circumferential points would have to map to a line). This is treated below by scaling 1-100% instead of 0-100%.
Let me again touch on the subject of conversion from polygons / lists of points to valid 3D solids.
When creating a hull, adjacent sections have to be linked with shells of triangles. As the end product is topologically the same as a block or sphere, the ends have to be closed (it's not a toroid) which is also handled by skin(). The latter just adds start and end faces and feeds the whole thing to polyhedron().
Merging with other geometry
The outsides generated by sections having [0,a],[0,b] vertical lines are not quadrilaterals but pairs of triangles which *should* be co-planar to the faces of cylindrical walls. Depending on the number of facets and overall make-up of the geometry this seems to be a hit-and-miss thing with CGAL. One way to avoid the butt joint problem and infinitesimal gaps is to let the parts interfere (approx. -0.05). My preferred way of doing that is to make the minor(major) diameter of the shaft (bore) a tad larger (smaller) to interfere with the thread form.
Usage:
union(){
straight_thread(
section_profile = bottle_pco1881_nut_thread_profile(),
higbee_arc = 20,
r = bottle_pco1881_nut_thread_major()/2,
turns = nut_turns,
pitch = bottle_pco1881_nut_thread_pitch(),
fn = $fn
);
// ... the rest of your geometry here
}and that's all folks.
Other approaches:
turns out "tornillo" is the spanish word for screw/bolt. If you're looking for ISO metric threads (threadAngle = 30) or ACME (threadAngle = 29), this might be for you:
https://github.com/KaliNuska/Curso_2015-2017/blob/master/TIC/Imagen%20Vectorial.md
Part of the purpose to my effort to create nice threads in a generalized way is to become more familiar with OpenSCAD and the ways it wants to be used. If you've done something similar I apologize for not giving credit where due. Please drop a few lines in the comments.
 helge
helge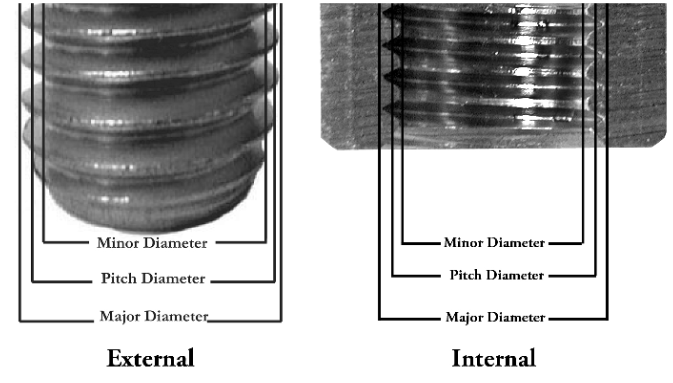
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
This is a beautiful and elegant solution. The general problem of making threaded matings is usually something I've done in FreeCAD but this actually makes it easier and more transparent. Looking at the demo comment in thread_profile.scad was helpful, then I figured out the profile was just the XZ plane coordinates of the thread cross-section. A key point is that the pitch must be greater than the overall height of the profile, which is not a problem for bottle threads and whatnot but will potentially create shapes that CGAL will not render.
Are you sure? yes | no
My OpenSCAD Revolve2 library can do pretty much any kind of threading, including multiple threads and spiraling threads. It does the triangulation on the fly generating properly oriented polyhedrae, which means that they won't crash when used in boolean ops. Ah it is also blazingly fast. Curiously it was just about few months younger than this post, which I have noticed just now. https://www.thingiverse.com/thing:3215997
Are you sure? yes | no
A couple years ago I had done the PET bottle thread painfully in Tinkercad using the exact PCO-1881 specs, back when Tinkercad had the ability to create Javascript shape generators, but I've moved on to OpenSCAD and found your article. This will save me the trouble of doing it again. Looks like all I need to do is put in my thread profile (the one in your file isn't optimized for 3D printing; there is only one pressure face, and the other can be a 45-degree slope overhang, which gives a stronger plastic thread).
Are you sure? yes | no
Are you able to graphically explain the different settings? I'm looking to add Nalgene wide mouth bottles to the list of thread profiles, but I'm having difficulty understanding the values I need to enter.
Are you sure? yes | no
I'll see what I can come up with until the weekend. You're right, there should be a visual guide to constructing new profiles.
As a quick attempt, let me point out that the radius given for both inward-facing thread geometry (for the nut, added to a clindrical hole) and outward facing geometry (threads added to a cylindrical shaft or pipe) corresponds to the neutral plane were the profile considered to be a long prism bent into a ring. Thus the thread profile (given as a 2D polygon) is specified relative to that radius, e.g.
r = bottle_pco1881_nut_thread_major()/2
the radius is usually the internal thread major radius or external thread minor radius.
Are you sure? yes | no
As an OpenSCAD convert myself, I really like and appreciate what you did here. Building basically the perfect polygon from scratch like this was not an easy task.
Given I can't like it twice, thought I would say so in person. Thank you, and good job.
Are you sure? yes | no
Thank you :)
I had a bit of a bumpy start with OpenSCAD but seeing now that I might have contributed something that helps others is more than rewarding.
Are you sure? yes | no
Nice work! Thanks for sharing.
I have tabularized a number of standard threads (currently limited to BSP-parallel) and created a library to build threads by simply specifying a designator (e.g. "G 1/2-ext"). It uses your thread_profile.scad to do the main work.
See here: https://github.com/adrianschlatter/threadlib
Are you sure? yes | no
Beautiful work, thanks for also referencing the background article.
Maybe you could add a few renders of the threadlib capabilities and add them to the repository readme :)
Are you sure? yes | no
Good point, I'll do that.
Are you sure? yes | no
I tried solving the same problem and ended up rotate-extruding an archimedian spiral: https://www.thingiverse.com/thing:2076289
Are you sure? yes | no
interesting - while this approach doesn't generate the severely serrated surfaces there are still a lot of high aspect ratio facets and way more faces than necessary. If I'm not mistaken the serration problem is basically attenuated by the high polygon count.
Detailed view of the linked model: https://abload.de/img/geometry_details76c10.png
A way to benchmark the two methods side by side would be the run time for the calculation of boolean operators and anecdotal observation of flaws / errors resulting from the model geometry.
Are you sure? yes | no