In Part 5, we considered a simple circuit formed from a 5 V battery, a resistor, and two pieces of copper wire. We also introduced the concept of Ohm’s law, which describes the relationship between voltage (V), current (I), and resistance (R).
 A simple circuit comprising a battery, a resistor, and two pieces of wire (Image source: Max Maxfield)
A simple circuit comprising a battery, a resistor, and two pieces of wire (Image source: Max Maxfield) At the end of the column, we noted that we qualified the resistors shown in the first image as being “0.25 watt resistors.” (We might also write this as “1/4 watt resistors;” in conversation, we would say “quarter watt resistors”.) Well, now it’s time to explain what we meant by this.
Feel the Power!
Electric power (P) is the rate, per unit time, at which electrical energy is transferred by an electric circuit. The SI unit of power is the watt, with a symbol of ‘W,’ which is named after James Watt (1736 -- 1819), who was a Scottish inventor, mechanical engineer, and chemist.
In the case of resistive circuits (a.k.a. Ohmic or linear loads), the equation for power can be expressed as:
P = IV
Where P = power, V = voltage, and I = current. We might also write this as:
P = I*V or P = I × V
Irrespective of how we write this equation, P is measured in watts, I is measured in amps, and V is measured in volts.
Now, from Ohm’s law, we have the following three versions of his equation to play with:
V = IR (used to calculate voltage if we know current and resistance)
I = V/R (used to calculate current if we know voltage and resistance)
R = V/I (used to calculate resistance if we know voltage and current)
Thus, we could substitute for V in our power equation as follows:
P = I * V
and V = I * R
so substituting V gives us P = I * (I * R)
resulting in P = I2R
Similarly, we could substitute for I in our power equation as follows:
P = I * V
and I = V/R
so substituting I gives us P = V/R * V
resulting in P = V2/R
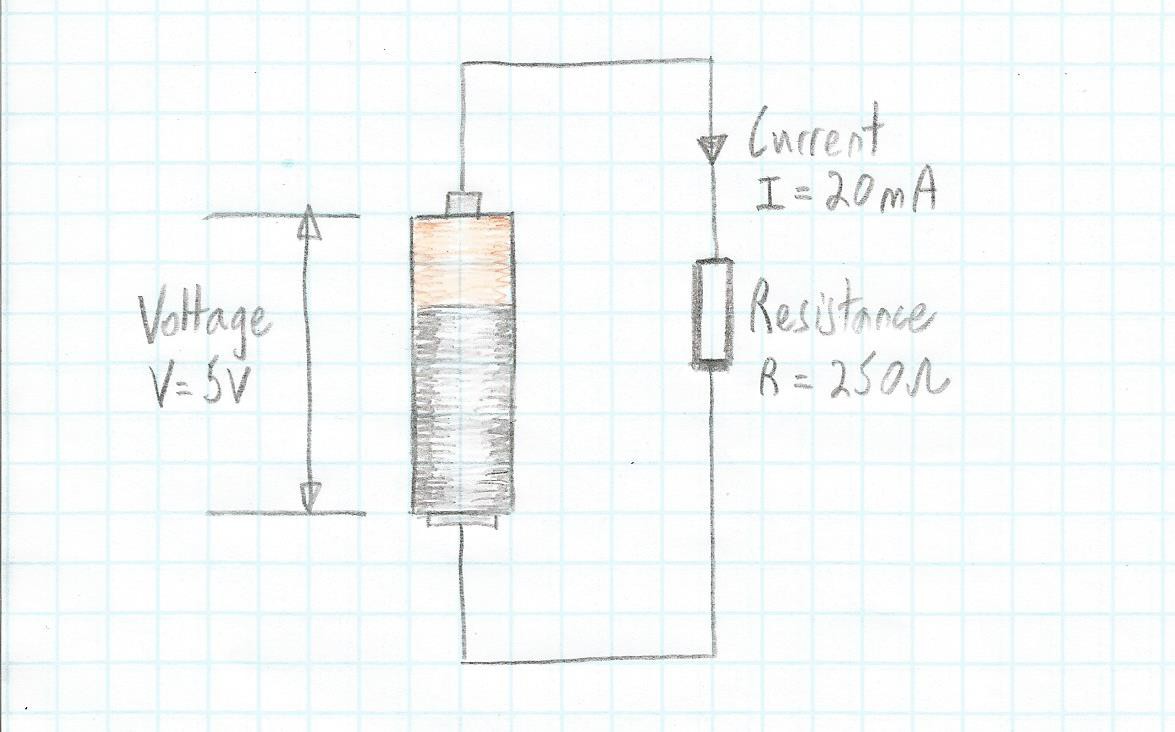
As an example, let’s consider the circuit we showed earlier, remembering that we have to work in units of volts, amps, ohms, and watts, and that 20 mA (twenty milliamps) equates to 0.02 A.
P = I * V
P = 0.02 * 5
P = 0.1 W or 100 mW
As we see, in this case, the amount of power that has to be handled by the resistor is 0.1 W or 100 milliwatts (mW).
Why don’t you try performing similar calculations for yourself, but instead of using V and I, first use V and R, then use I and R. Obviously you should see the same 0.1 W (100 mW) result in all cases.
The bottom line is that, knowing any two of the P, V, I, R values in a resistive circuit provides you with enough information to derive the other two quantities.
In the same way that we graphically represented all of the versions of Ohm’s law as Ohm’s triangle in Part 5, we can gather all of the permutations of our P, V, I, R calculations in the handy-dandy graphic shown below.
 The P, V, I, R circle (Image source: Max Maxfield)
The P, V, I, R circle (Image source: Max Maxfield) As one final point, when we use resistors in our circuits, it’s important to ensure that they are rated to carry the power we require them to handle. For the low-power circuits we’ll be playing with, 0.25 W (1/4 W) resistors will usually fit the bill, but it’s important for us to do the math before we flip the power switch to its “On” position, otherwise we may find ourselves living in interesting times.
 max
max
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.