In the not-so-distant future, we’re going to start creating simple circuits using resistors and light-emitting diodes (“Ooh, Shiny!”). However, in order to warm ourselves up for this awesome experience, we first need to learn a little more about resistors to ensure that we use the right ones when the occasion arises.
Before we start, I’m going to make the assumption that you’ve read the previous columns in this series, which means you should have at least a vague idea as to what a resistor is and what it does. If not, this would be a really good time to do so (LOL).
Also, before we start, a small word of warning. Do you remember being introduced to the concept of logarithms at school? Did you enjoy meeting them as much as I did (which is to say, not a lot)? Well, I’m afraid we are going to lightly touch on them here, but you don’t need to worry because it’s not going to hurt (me) at all.
As an aside, if you aren’t comfortable with logarithms, which were introduced by the Scottish mathematician, physicist, and astronomer John Napier in 1614 as a means of simplifying calculations, then this would be a great topic for you to read up on in your own time, because they have all sorts of cool attributes and uses (you might also want to check this Intro to Logarithms Video from the Khan Academy).
Different Types of Resistors
Resistors can be created from a wide variety of materials using a multiplicity of techniques. If you hang out with dubious people in strange places, you may hear talk of Carbon Composition, Carbon Film, Ceramic, Metal Element, Metal Film, Metal Foil, Metal Oxide Film, Thick Film, Thin Film, and Wirewound resistors (and I wouldn’t be surprised to discover that I’ve left some out).
Each type of resistor has its own advantages and disadvantages. For example, one type of resistor may cost more than another, but its resistance may not vary as much with changes in temperature, which may be an important attribute for a particular application. Happily, for what we are doing here, we really don’t have to worry about any of this. For the purposes of these columns, we are going to use the cheapest, most common resistors we can lay our hands on (I’ll guide you in this later).
Standard Resistor Values (a Little History)
As we will come to see in future columns, when we design an electronic circuit, we may perform some calculations, wave our hands in the air, perform an interesting dance, and decide that -- in an ideal world -- we would like to use a resistor with a value of exactly X ohms.
One solution would be to handcraft individual resistors with whatever values we wish, but this would be resource-intensive and time-consuming, to say the least. Alternatively, it would potentially be possible for resistor manufacturers to offer bespoke services where we tell them what we want and they build to order (BTO), but this would take lots of time and be tremendously expensive. Furthermore, neither of these options work well if the intention is to create large numbers of products with interchangeable parts.
What we really need is access to affordable, off-the-shelf resistors that are available when we require them. Unfortunately, the folks who manufacture resistors simply cannot create and supply every conceivable value in a cost-effective manner. And, even if every possible value was available, the people who use resistors couldn’t afford to purchase all of the different types and wouldn’t have the space required to store them if they did.
The solution arrived at by the industry was to adopt a selection of standard values, which had the added advantage of allowing users to second-source their resistors from multiple manufacturers. The real trick was for everyone to agree on the values forming the standard set.
Before we proceed, there’s an important topic we need to introduce, which is that of “tolerance.” In this context, tolerance refers to the limits of variation of a resistance value. These days, advances in manufacturing mean that it's typically possible to create things pretty close to where we want them to be. This wasn’t the case in the not-so-distant past when things were generally much slacker when it came to our ability to create components “just so.”
Let’s go back in time to when a manufacturing tolerance of 30% was considered to be a “pretty good show.” What this means is that if we were to create a bunch of resistors aiming at a value of 1 ohm with a ±30% tolerance, then their values would actually be spread out between 0.7 and 1.3 ohms. In turn, this means that there would be no point in us specifically trying to manufacture a resistor of 1.15 ohms, for example, because there is a good chance that we could find one in our 1 ohm ±30% batch.
On this basis, what we need to do is to determine the optimal set of resistors-plus-tolerances that will cover each decade (1 to 10, 10 to 100, 100 to 1,000, 1,000 to 10,000, etc.). Now, our knee-jerk reaction might be to try to divide each decade up in a linear manner -- that is, into equal parts -- but it turns out this doesn’t offer the best solution. In the same way that a bunch of 1 ohm ±30% resistors will give us a range between 0.7 and 1.3 ohms (a spread of 0.6 ohms), so too will a bunch of 10 ohm ±30% resistors give us a range between 7 and 13 ohms (a spread of 6.0 ohms). As we see, the spread is an order of magnitude larger at the high-end of the decade. Based on this, dividing things up in a linear fashion would require us to use more values than we really want.
This leads us to the concept of “preferred numbers” (also called “preferred values” or “preferred series”), which are standard guidelines used in industrial design for choosing exact product characteristics within a given set of constraints. One of the aspects of preferred numbers is that they are chosen such that when a product is manufactured in many different sizes, these sizes will end up roughly equally spaced on a logarithmic scale. By this means, preferred numbers help to minimize the number of different sizes that need to be manufactured and/or kept in stock.
A French military engineer called Charles Renard worked all of this out and proposed a set of preferred numbers in 1877. In Renard's system, the interval from 1 to 10 was divided into 5, 10, 20, or 40 steps, which we now refer to as the R5, R10, R20 and R40 scales. Let’s start by taking the R5 scale as an example. One way to represent this mathematically is as follows (where the symbol ≈ means “approximately equal to”):
10(0/5) = 1
10(1/5) = 1.584... ≈1.6
10(2/5) = 2.511... ≈2.5
10(3/5) = 3.981... ≈4.0
10(4/5) = 6.309... ≈6.3
10(5/5) = 10
Another way we can look at this is graphically as shown below. Since this scheme is based on a logarithmic approach, observe that each new number can be generated by multiplying the previous value by 10(1/5) = 1.584 and rounding as required.
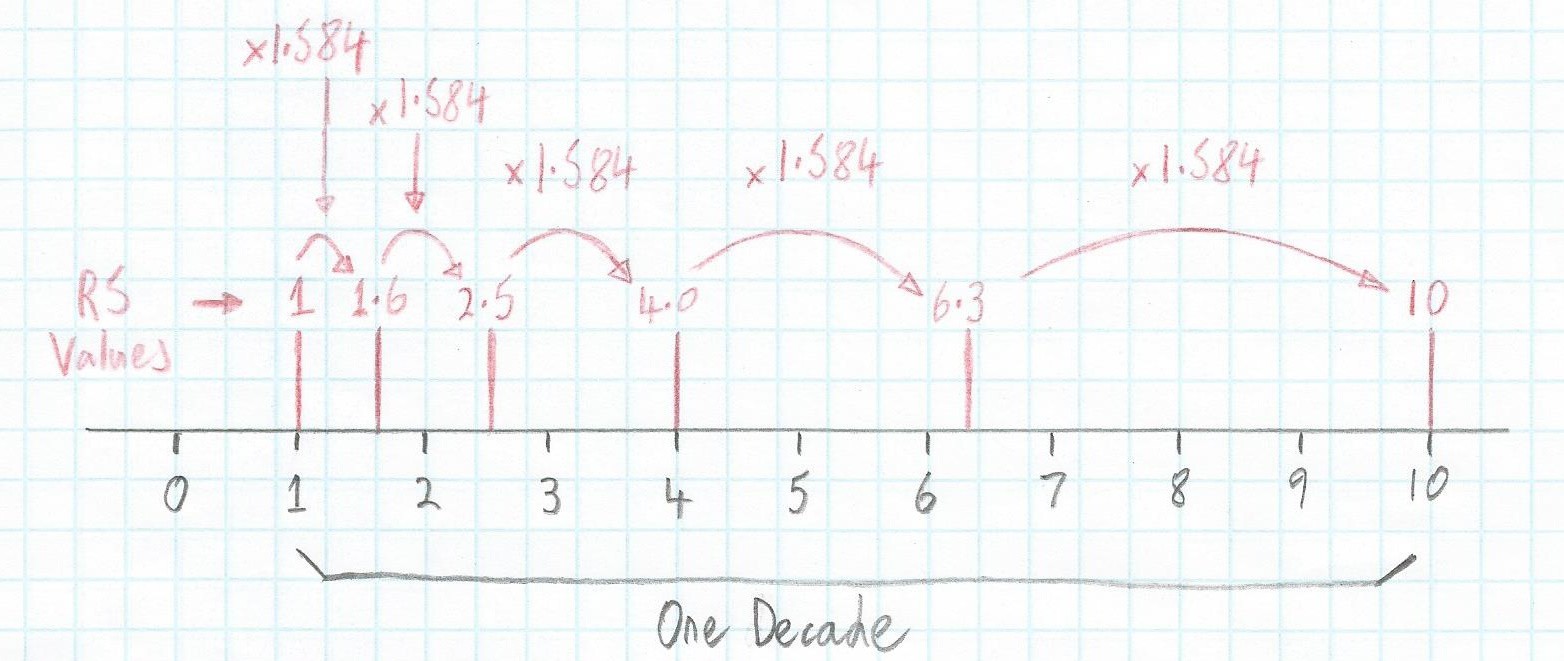 A graphical representation of the R5 scale (Image source: Max Maxfield)
A graphical representation of the R5 scale (Image source: Max Maxfield) One great thing about this logarithmic approach is that we can repeat it decade by decade; that is, the example above was for the decade 1 to 10, but exactly the same thing applies for the decade 10 to 100, and so forth. By means of this geometric sequence, the maximum relative error is minimized if an arbitrary number is replaced by the nearest Renard number multiplied by the appropriate power of 10.
Another cool aspect associated with this logarithmic approach is that if we have components that can be manufactured with a tighter tolerance and we decide to move to a higher resolution scale, then the values from the lower resolution scale also appear in the more comprehensive scale. Take the R10 scale for example:
10(0/10) = 1 (Same as for the R5 Scale)
10(1/10) = 1.258... ≈1.3
10(2/10) = 1.584... ≈1.6 (Same as for the R5 Scale)
10(3/10) = 1.995... ≈2.0
10(4/10) = 2.511... ≈2.5 (Same as for the R5 Scale)
10(5/10) = 3.162... ≈3.2
10(6/10) = 3.981... ≈4.0 (Same as for the R5 Scale)
10(7/10) = 5.011... ≈5.0
10(8/10) = 6.309... ≈6.3 (Same as for the R5 Scale)
10(9/10) = 7.943... ≈7.9
10(10/10) = 10 (Same as for the R5 Scale)
Once again, since this scheme is based on a logarithmic approach, observe that each new number can be generated by multiplying the previous value by 10(1/10) = 1.258 and rounding as required.
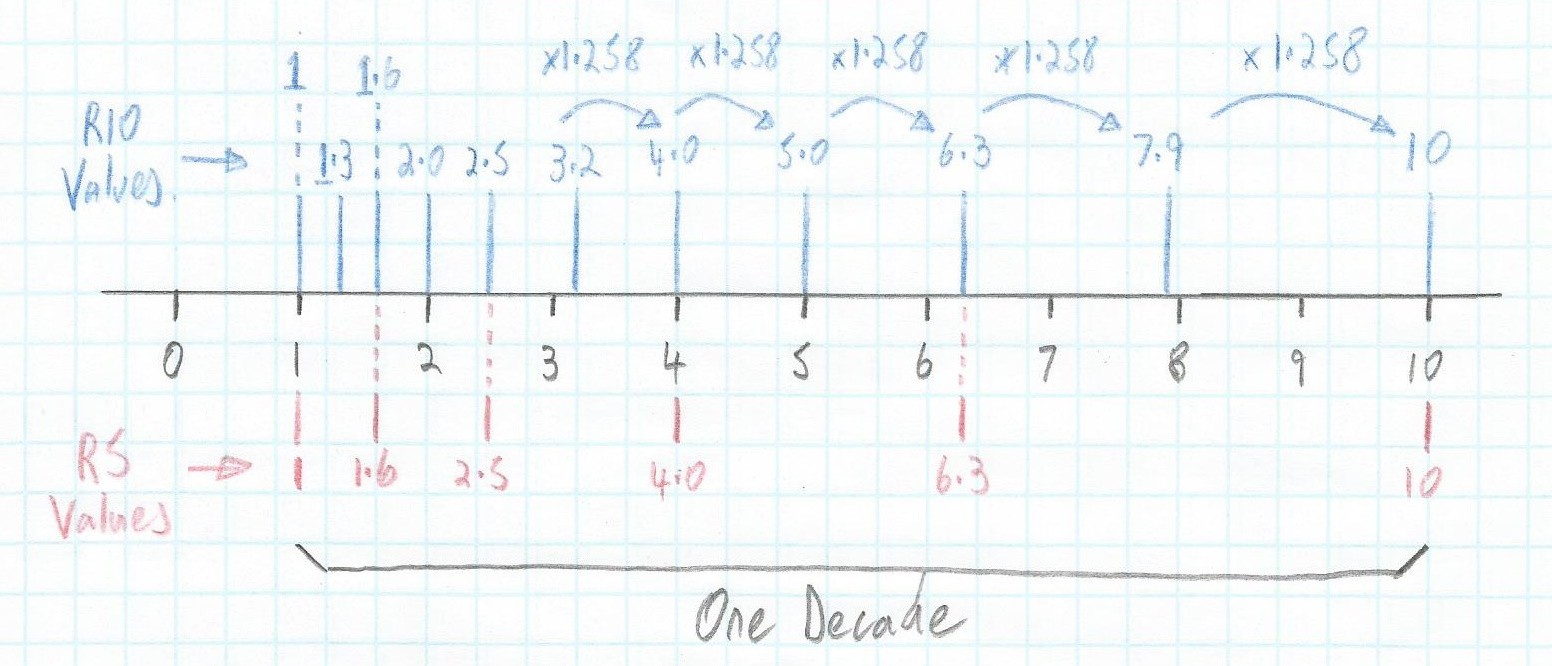 A graphical representation of the R10 scale (Image source: Max Maxfield)
A graphical representation of the R10 scale (Image source: Max Maxfield) I don’t know about you, but I find this to be staggeringly clever, and it amazes me that Renard came up with it back in 1877. It’s also interesting to me that Renard didn’t actually conceive his system in the context of electronics. As it happened, Renard was tasked with reducing the number of different types of ropes used by the French army with regard to their collection of balloons. We aren’t talking about small party balloons, of course, but rather the large human-carrying balloons used to spy out enemy positions and drop bombs on anyone who criticized French cuisine (remember that these are the people who, around 100 years later in the 1960s, came up with the idea of presenting a platter bearing a sliver of meat, two small potatoes, and three artfully arranged peas, calling it “nouvelle cuisine,” and charging you an exorbitant sum for the privilege of feasting your eyes, if not your tummy).
But we digress... When Renard initially turned his attention to the task, in order to keep their balloons in the air, the army was obliged to maintain 425 different sizes of ropes, which was a logistical nightmare. Using his preferred numbers, Renard managed to reduce this number to only 17 sizes that covered the same range. Not surprisingly, this made him the “toast of the town” with army quartermasters. Sad to relate, however, Renard was never again to be invited to a soiree hosted by the rope maker’s guild.
Renard’s R5, R10, R20 and R40 scales were officially adopted as standards by the International Organization for Standardization (ISO) in the early 1950s and are employed by various disciplines. In the case of electronics, for example, they are used for such applications as the current rating of electric fuses and the voltage rating of capacitors (e.g., 100 V, 160 V, 250 V, 400 V, 630 V).
Sad to say, Renard’s scales aren’t used for resistors. “What!?! In that case, why have you spent so much time waffling on about them,” I hear you cry. Well, these discussions have set the scene for what is to come in our next column, in which we will introduce the preferred values we do use for resistors. In the meantime, as always, I welcome your comments, questions, and suggestions.
 max
max
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
[this comment has been deleted]
I'm delighted if my columns are really what you are looking for, but confused as to why you would include a URL for a Stucco company in California -- do you really think seeing this URL in a comment to a column on beginning electronics will make anyone say "My gosh, I really need a Stucco company, and how convenient that this one is in the same state (or country) as me!"
Are you sure? yes | no
Now you have left me in the dark until the next Article... Respect for Renard nevertheless!...
Are you sure? yes | no
I'm sorry about that -- this column was "growing in the telling" as they say, and I'm trying not to have too much in each column because I want readers to be able to wrap their brains around each topic before moving on to the next. It amazes me that Renard came up with this stuff back in 1877.
Are you sure? yes | no
Guess at age 63 I still find I do not know everything. This was something I did not know about but just took the standard values for granted and never gave much thought as to how they were decided on :-)
Are you sure? yes | no
You and me both -- I knew that the standard values were logarithmic in nature, but until I started to explain it here, I never knew why. In my next column I will be talking about the E-series we DO USE for resistors -- I guess I could have skipped this column and gone directly into the next one -- but I love knowing where things came from and why we do things the way we do -- also, I think this really fits in with the spirit of this series of columns building a strong foundation of understanding.
Are you sure? yes | no