The Effect of Particle Size

h1>The Effect of Particle Size


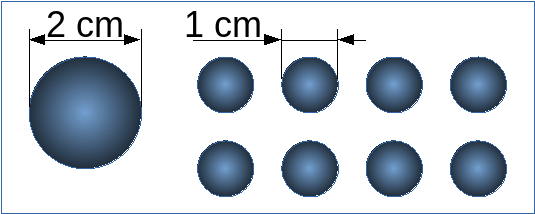
Compare a large and a small sphere.

The diameter of the large sphere is double that of the small sphere.

The area of the large sphere is four times that of the small sphere.

The volume of the large sphere is eight times that of the small sphere.

It takes eight small spheres to have the same volume as the large sphere.

Compared to the large sphere, the total target area of the small spheres will be (1/4 x 8 = 2) twice
the target area of the big sphere.

So, for a given volume of colloidal particles, the probability of a photon collision changes a lot d
epending on the diameter of the colloidal particles.

The Experiment

We have data for two sets of colloidal dispersions, dilute milk, and diatomaceous earth. We found a
case in which the scattering curves are roughly the same for both.



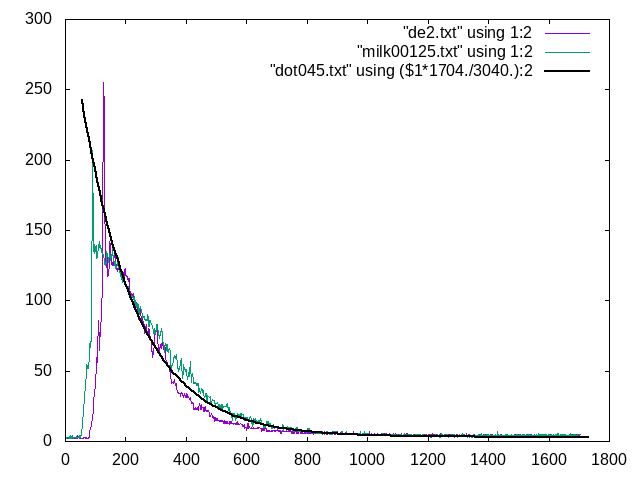
On those two curves we overlaid a calculated curve for a probability of collision of p = 0.045.



We have reliable data for the size of milk fat particles in 2% homogenized milk (diameter = 0.8 um)
. We used that to calculate the target size for photon collisions. The result was that milk fat partic
les covered 0.047 of the total surface area on which the laser shone. That agrees well with the p = 0.0
45 curve that overlaid the measured scattering curve.



Diatomaceous earth has particle diame
ters ranging from 10 um to 200 um. Based on the match between the curves, we assumed the diluted diatom
aceous earth dispersion had about the same probability of photon collision as the milk and the theoretic
al curves. A particle size with a diameter of 25 um produced that result.



To produce the same scattering as milk fat, diatomaceous earth (DE) required forty times the volume.
(ie. milk fat 0.005 ml in 200 ml water vs. DE 0.2 ml in 200 ml water.) The difference is plausibly e
xplained by the difference in particle size.

Calculations

Python3 code

=====================================



def prn(caption, i):

    print(caption,'{:g}'.format(float('{:.{p}g}'.format(i, p=3))))



from math import pi



#calculate milk, volume of fat in 200 ml

fv = 0.02 * 200



#calculate de volume in 200 ml

dev = 1.25 * 200./250.



#calculate volume of fat in dot00125 solution

dfv = fv * 0.00125



#calculate volume of de in dot2 solution

ddev = dev * 0.2



#prn("dilute volume of fat", dfv, "ml")

#prn("dilute volume of de", ddev, "ml")

prn("dilute volume of fat (ml)", dfv)

prn("dilute volume of de (ml)", ddev)



prn("ddev / dfv", ddev/dfv)



totalMl = 250. #we made 250 ml of fluid

totalMm3 = totalMl * 1000.



deDiaM = 25e-6 #meters

deDiaMm = deDiaM * 1000.

deRadMm = deDiaMm / 2

prn("DE radius (mm)", deRadMm)

totalMl = 250. #we made 250 ml of fluid

totalMm3 = totalMl * 1000.

#deConc = 1.25 ml x 1000 mm3/ml * 200 ml / 250 ml

#started with 250 ml distilled water. cylinder volume = 200 ml

#the sample was diluted with distilled water.

#the undiluted sample was 20% of the final diluted sample

deVolMm3 = 0.2 * (1.25*1000*200./250.) #DE volume in cubic mm of test sample

deVolPerMm3 = deVolMm3 / totalMm3 #DE volume per cubic mm

prn("DE volume per cubic mm", deVolPerMm3)

deSphereVol = (4./3.) * pi * deRadMm**3 #de sphere in cubic mm

prn("DE sphere volume (mm^3)", deSphereVol)

noDeSpMm3 = deVolPerMm3 / deSphereVol #number of DE spheres per cubic mm

prn("number of DE spheres per cubic mm", noDeSpMm3)

deAopS = pi * deRadMm**2 #DE area occluded per sphere in square mm

prn("DE area occluded per sphere (mm^2)", deAopS)

deAo = deAopS * noDeSpMm3

prn("DE area occluded", deAo)



mfDiaM = 0.8e-6 #meters

mfDiaMm = mfDiaM * 1000.

mfRadMm = mfDiaMm / 2

prn("milk fat radius (mm)", mfRadMm)

totalMl = 200. #200 ml sample in graduated cylinder

totalMm3 = totalMl * 1000.

#from above, volume of milk fat in dilute solution = dfv

mfVolPerMm3 = 1000 * dfv / totalMm3 #DE volume per cubic mm

prn("milk fat volume per cubic mm", mfVolPerMm3)

mfSphereVol = (4./3.) * pi * mfRadMm**3 #mf sphere in cubic mm

prn("milk fat sphere volume (mm^3)", mfSphereVol)

noMfSpMm3 = mfVolPerMm3 / mfSphereVol #number of milk fat spheres per cubic mm

prn("number of milk fat spheres per cubic mm", noMfSpMm3)

mfAopS = pi * mfRadMm**2 #milk fat area occluded per sphere in square mm

prn("milk fat area occluded per sphere (mm^2)", mfAopS)

mfAo = mfAopS * noMfSpMm3

prn("milk fat area occluded", mfAo)



=======================================================

Results

dilute volume of fat (ml) 0.005

dilute volume of de (ml) 0.2

ddev / dfv 40

DE radius (mm) 0.0125

DE volume per cubic mm 0.0008

DE sphere volume (mm^3) 8.18e-06

number of DE spheres per cubic mm 97.8

DE area occluded per sphere (mm^2) 0.000491

DE area occluded 0.048

milk fat radius (mm) 0.0004

milk fat volume per cubic mm 2.5e-05

milk fat sphere volume (mm^3) 2.68e-10

number of milk fat spheres per cubic mm 93300

milk fat area occluded per sphere (mm^2) 5.03e-07

milk fat area occluded 0.0469