-
Laser Calibration 2
01/26/2021 at 02:58 • 0 commentsLaser Power Calibration using Camera
based on camera specifications
The Equipment Setup
The setup is shown in the image below.
![]()
Shining a laser directly into the lens of a camera is probably a bad idea.
By scattering the laser beam and then taking advantage of the inverse square law, we can get any attenuation we want.
A Lambert surface scatters light in a predictable manner. Paper can make a good Lambertian surface. link We had some paper that matched the description of what was used in the link.
We imagine a hemisphere centered on the point at which the laser beam strikes the paper. If we know the radiant flux density (watts per square meter) on the surface of the sphere directly above the paper, we can predict what it should be anywhere else on the surface of the hemisphere.
E' = E cosθ
Where:
E is the radiant flux density on the surface of the hemisphere
exactly above the middle of our Lambertian surface.
E' is the radiant flux density at the camera lens.
θ is the angle between the reference point and the camera lensThe process will go as follows:
- Calculate the power received by the camera.
- Calculate the power at the reference point on our imaginary hemisphere.
- Figure out how the power on the reference point relates to the laser power.
- Calculate the laser power it took to create the power at the reference point.
Calculate the Power Received by the Camera
The camera was set up such that a picture could be taken of the scattered laser light without saturating.
The aperture was left wide open. The analog gain was set to unity. The exposure time was 1/1000 second.
Full Well Capacity (FWC) = 8180 #taken from Strolls with my Dog
The data from the camera was surprising so a total of four images was taken with the paper being rotated between each image.
The surprise is how much the energy seems to be concentrated in the middle of the laser beam.
Based on an initial guess about the width of the laser beam, the statistical calculations were based on 1 mm cubes.
With the equipment set up as it is, 1 mm at the center of the graduated cylinder is about 14 pixels at the camera.
fwc = 8180. #full well capacity
mdn = 255. #max digital number
f = open("ave.txt", 'r')
total = 0
l = f.readline()
while l != "":
pos = l.find(" ")
num = int(l[pos:])
total = total + num
l = f.readline()
#that's for an array 15 x 1
#to get a 1 mm square area multiply by 206/15
total = total * 206./15.
f.close()
print(total)
#the red pixels are 1/4 of the total pixels
#to get the correct energy landing on the 1 mm square,
#multiply the electrons by four
electrons = 4 * int(fwc * total / mdn)
print("electrons", electrons)
h = 6.6e-34
c = 3e8
lmbda = 640e-9
ee = h*c/lmbda #electron energy (joules)
print("electron energy", ee, "joules")
eas = electrons * ee #energy at sensor (joules) per 1 mm square
print("energy at sensor", eas, "joules")
The result is:
6743.066666666667
electrons 865228
electron energy 3.09375e-19 joules
energy at sensor 2.676799125e-13 joules
How does the Power at the Reference Point Relate to the Laser Power?
A numerical model was constructed for the hemisphere. The reference point was taken as 1 unit and the power illuminating the surface of the hemisphere was calculated. That provides a ratio between the reference point power and the laser power.
The hemisphere was modelled as a stack of rings of varying radius. The inner surface of each ring was 1 mm wide so the inner surface area of each ring would be 1 mm x 2 * pi * r where r is in mm.
![]()
The total power illuminating each ring would be the ring area x cosθ. In the following code, angle α was used to calcualte each ring radius so the power illuminating the ring would be cos(90° - α).
#a set of stacked rings approximating a hemisphere
Read more
#the power... -
Laser Calibration 1
01/26/2021 at 02:46 • 0 commentsLaser Power Calibration
If we're going to do anything useful with our test setup, it's necessary to know the power of our laser.
We used four methods to measure the laser power. Each of the methods has its 'issues' but they agree closely enough to give us some confidence in the results.
Method Laser Power Light Dependent Resistor
compared with bright sunlight0.1 mw Photodiode
compared with bright sunlight0.15 mw Photodiode
based on specifications0.27 mw Camera
based on specifications0.1 mw
Light Dependent Resistor (LDR)
We compare the response of a LDR to the laser and to the bright sun.
Why the sun?
The sun is close to being a reliable standard illuminator.
The sun and a low power laser have about the same irradience, approx
imately one milliwatt per square millimeter.
The illumination of the bright sun can be calculated for any time of day, for any day of the year, and for any latitude. link
The resistance of the LDR varies roughly inversely with the power of the incident light.
The Setup
The Light Dependent Resistor (LDR) was mounted behind a 7/64 diameter aperture. When the laser was shone through the apert
ure, the hole was slightly fringed with red light. The intent was that light from the sun and light from the laser would illum
inate the same area on the surface of the LDR.
Results
Resistance due to laser light: 148.2 ohms
Resistance due to sunlight: 20.1 ohms
Sunlight power per square mm: 0.75 mw
laser power = 0.75 x 20.1 / 148.2 = 0.1 mw
Photodiode
compared with bright sunlightThe current of the photodiode is roughly proportional to the number of photons striking it. The sensitive area is a 1 mm s
quare.
Results
Current due to laser light: 0.081 ma
Current due to sunlight: 0.393 ma
laser power = 0.75 x 0.081 / 0.393 = 0.15 mw
Comment
The photodiode has a huge variation in sensitivity across the spectrum of solar radiation. It is highly biased toward the
red end of the visible spectrum and near infrared. This calculation above ignores that fact.
Photodiode
using specificationsThe datasheet gives a figure
for quantum yield (0.9 at 850 nm) plus a graph of relative sensitivity vs. wavelength.
For 640 nm (the wavelength of the laser) the electrons generated per photon is: 0.9 x 75% = 0.675.
Calculations
The calculations for this section and the next are based on:
1 - Lumenera
2 - Strolls with my Dog
Strolls with my Dog has done excellent work uncovering the technical details of the Raspberry Pi High Quality Camera.
The following is from a jupyter notebook. It's mostly python3 code but also includes the results of print statements.
#laser wavelength
lmbda = 640e-9
#diode spectral sensitivity per datasheet
ss = 0.75
#measured current (ma)
i = 0.094e-3
#coulomb
cou = 6.24e18
#electrons per second
eps = i * cou
#conversion @ 850 nm electrons per photon
n = 0.9
#photons produced by laser beam
pp = eps / (n * ss)
#energy per photon e = h v = h c / lmbda
h = 6.63e-34
c = 3e8
ep = h * c / lmbda
#energy (watts) = photons per second x energy per photon
pwr = pp * ep
print("Laser Power = ", round(pwr*1000,2), "mw")
Laser Power = 0.27 mw
Using the Camera to Calibrate the Laser
That's sufficiently complicated that it merits its own page. link
-
The Effect of Colloid Particle Size
01/06/2021 at 19:17 • 0 commentsThe Effect of Particle Size
h1>The Effect of Particle Size
![]()
Compare a large and a small sphere.
The diameter of the large sphere is double that of the small sphere.
The area of the large sphere is four times that of the small sphere.
The volume of the large sphere is eight times that of the small sphere.
It takes eight small spheres to have the same volume as the large sphere.
Compared to the large sphere, the total target area of the small spheres will be (1/4 x 8 = 2) twice
the target area of the big sphere.
So, for a given volume of colloidal particles, the probability of a photon collision changes a lot d
epending on the diameter of the colloidal particles.
The Experiment
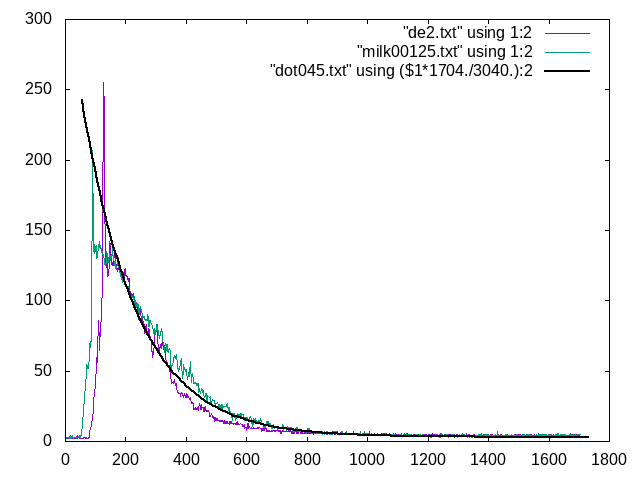
We have data for two sets of colloidal dispersions, dilute milk, and diatomaceous earth. We found a
case in which the scattering curves are roughly the same for both.
![]()
On those two curves we overlaid a calculated curve for a probability of collision of p = 0.045.
We have reliable data for the size of milk fat particles in 2% homogenized milk (diameter = 0.8 um)
. We used that to calculate the target size for photon collisions. The result was that milk fat partic
les covered 0.047 of the total surface area on which the laser shone. That agrees well with the p = 0.0
45 curve that overlaid the measured scattering curve.
Diatomaceous earth has particle diame
ters ranging from 10 um to 200 um. Based on the match between the curves, we assumed the diluted diatom
aceous earth dispersion had about the same probability of photon collision as the milk and the theoretic
al curves. A particle size with a diameter of 25 um produced that result.
To produce the same scattering as milk fat, diatomaceous earth (DE) required forty times the volume.
(ie. milk fat 0.005 ml in 200 ml water vs. DE 0.2 ml in 200 ml water.) The difference is plausibly e
xplained by the difference in particle size.
Calculations
Python3 code
Read more
=====================================
def prn(caption, i):
print(caption,'{:g}'.format(float('{:.{p}g}'.format(i, p=3))))
from math import pi
#calculate milk, volume of fat in 200 ml
fv = 0.02 * 200
#calculate de volume in 200 ml
dev = 1.25 * 200./250.
#calculate volume of fat in dot00125 solution
dfv = fv * 0.00125
#calculate volume of de in dot2 solution
ddev = dev * 0.2
#prn("dilute volume of fat", dfv, "ml")
#prn("dilute volume of de", ddev, "ml")
prn("dilute volume of fat (ml)", dfv)
prn("dilute volume of de (ml)", ddev)
prn("ddev / dfv", ddev/dfv)
totalMl = 250. #we made 250 ml of fluid
totalMm3 = totalMl * 1000.
deDiaM = 25e-6 #meters
deDiaMm = deDiaM * 1000.
deRadMm = deDiaMm / 2
prn("DE radius (mm)", deRadMm)
totalMl = 250. #we made 250 ml of fluid
totalMm3 = totalMl * 1000.
#deConc = 1.25 ml x 1000 mm3/ml * 200 ml / 250 ml
#started with 250 ml distilled water. cylinder volume = 200 ml
#the sample was diluted with distilled water.
#the undiluted sample was 20% of the final diluted sample
deVolMm3 = 0.2 * (1.25*1000*200./250.) #DE volume in cubic mm of test sample
deVolPerMm3 = deVolMm3 / totalMm3 #DE volume per cubic mm
prn("DE volume per cubic mm", deVolPerMm3)
deSphereVol = (4./3.) * pi * deRadMm**3 #de sphere in cubic mm
prn("DE sphere volume (mm^3)", deSphereVol)
noDeSpMm3 = deVolPerMm3 / deSphereVol #number of DE spheres per cubic mm
prn("number of DE spheres per cubic mm", noDeSpMm3)
deAopS = pi * deRadMm**2 #DE area occluded per sphere in square mm
prn("DE area occluded per sphere (mm^2)", deAopS)
deAo = deAopS * noDeSpMm3
prn("DE area occluded", deAo)
mfDiaM = 0.8e-6 #meters
mfDiaMm = mfDiaM * 1000.
mfRadMm = mfDiaMm / 2
prn("milk fat radius (mm)", mfRadMm)
totalMl = 200. #200 ml sample in graduated cylinder
totalMm3 = totalMl * 1000.
#from above, volume of milk fat in dilute solution = dfv
mfVolPerMm3 = 1000 * dfv / totalMm3 #DE volume per cubic mm
prn("milk fat volume per cubic mm", mfVolPerMm3)
mfSphereVol = (4./3.) * pi * mfRadMm**3 #mf sphere in cubic mm
prn("milk fat sphere volume (mm^3)", mfSphereVol)
noMfSpMm3 = mfVolPerMm3 / mfSphereVol #number of milk fat spheres... -
Statistical Analysis of Colloid Project
01/04/2021 at 21:29 • 0 commentsStatistical Analysis
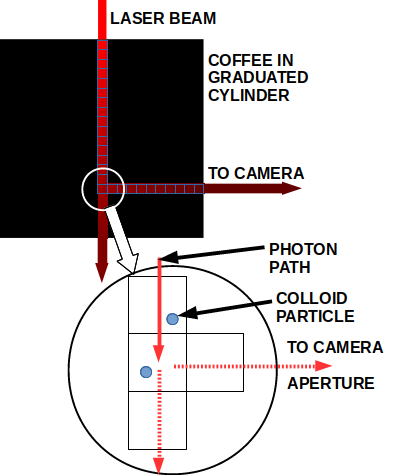
This analysis assumes that a photon undergoes one, and only one collision between the laser and the camera. It seems to work for our diluted coffee solutions (40 ml coffee in 160 ml distilled water). (I hasten to add that multiple collisions happen. This analysis doesn't cover them. There is a note at the bottom of the page about how to recognize the two situations.)
![]()
We divide the path of the laser beam into 1mm cubes.
There is a probability, p, that a photon will encounter a colloid particle and be reflected in some other direction.
Thus, the probability that the photon will make it to the next cube in line is 1 - p.
The probability that a photon will make it through a line of n cubes is (1-p)n
We will assume that a photon colliding with a colloid particle can be reflected in any direction, ie. that the collision is an omnidirectional radiator. (That is at odds with how light scattering in colloidal dispersions is conventionally described, especially for small particle sizes. Unless I've made an error, it seems to work as a first approximation. It doesn't work for a detailed calculation of signal strength. For that, you have to use MIE scattering.)
The probability that the photon will be reflected toward the aperture of the camera is small. It's a function of the area of the aperture and the distance between the camera and the reflecting colloid particle. It will be treated as a constant and ignored for the time being.Normalizing the Probabilities
We can graph the signal received at the camera from each point along the laser beam.
![]()
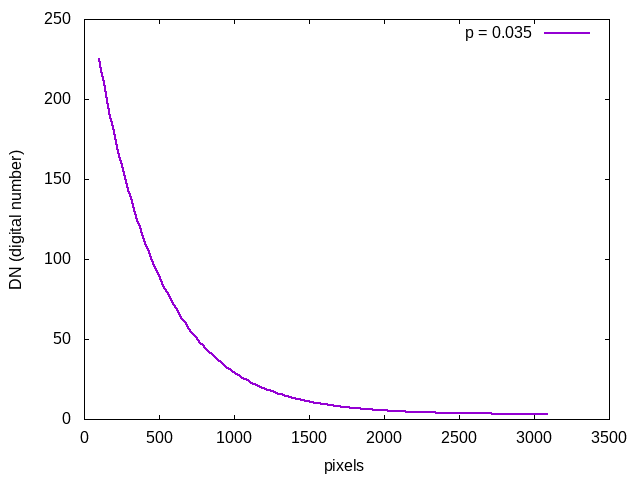
Note that each probability has a maximum value. In this case it is around 225.
The camera is set up such that the maximum value for a red pixel is 255. So, we don't want the maximum single reflection signal to exceed that. We can plot the maximum value for each probability against its p value.
We find a maximum DN of 246 for p = 0.056. We normalize the various probability curves such that their maxima lie on this curve. Does the Posited Theory Match the Measured Data?
The sample was 40 ml of coffee made in the MoccaMaster diluted with 160 ml of distilled water. A laser was shone down the middle of a graduated cylinder containing the sample. A picture was taken of the light scattered from the laser beam. The camera was a Raspberry Pi High Quality camera. The image format was RAW. Digital numbers (DN) representing the red pixels along the laser beam were extracted to a plot file.
In a subsequent page I will show that the p value is a function of the colloid concentration and the particle size.![]()
The above image is a graph of the digital numbers vs. their position (measured in pixels) along the laser beam. Note that the signal has a baseline noise of about 15 DN.
![]()
The above image is the left image plus a plot of the curve for p = 0.035.![]()
The above image has the two curves shifted. The measured data curve is shifted down to remove the effect of the baseline noise. The calculated curve is shifted right to remove the effect of the camera's alignment.Multiple Collisions
Multiple collisions can be detected by examining the picture of the illuminated sample. If any light shows away from the direct laser beam, it can only have been created as a result of more than one collision.
Back to Coffee Colloids Main Page