I'm Confused
Here's why:
 These two circuits are drawing the same current (26.3 μA) from 3V CR2032 batteries. The one on the right is driven with DC through a resistor adjusted to have the same average current drain as the pulsed version on the left (the PCB traces have been cut to isolate the LED from the rest of the circuit). The left appears much brighter than the right; to the eye, the difference is even greater than the photo captures - possibly for two reasons. First, the pixels in the center of the left LED are clipped at 255,255,255 in the image (over-exposed). Additionally, the camera doesn't show the possible physiological brightness enhancement due to pulsing. In either case, the conclusion one might draw from this image is that the version on the left is more electrically efficient, but the numbers don't check out!
These two circuits are drawing the same current (26.3 μA) from 3V CR2032 batteries. The one on the right is driven with DC through a resistor adjusted to have the same average current drain as the pulsed version on the left (the PCB traces have been cut to isolate the LED from the rest of the circuit). The left appears much brighter than the right; to the eye, the difference is even greater than the photo captures - possibly for two reasons. First, the pixels in the center of the left LED are clipped at 255,255,255 in the image (over-exposed). Additionally, the camera doesn't show the possible physiological brightness enhancement due to pulsing. In either case, the conclusion one might draw from this image is that the version on the left is more electrically efficient, but the numbers don't check out!
First, consider the DC-driven LED on the right. Electrical efficiency is easy to calculate in this case. The forward voltage (measured) across the LED at 26.3 uA is 2.031 V. At a battery voltage of 3.0 V, this means the electrical efficiency is just 2.031 / 3.0 = 67.7 %. It's not a terrible efficiency for a simple battery-resistor-LED circuit, but there's a problem. How is the LED on the left so much brighter? It seems more than twice as bright. This is, of course, impossible, since it would imply an electrical efficiency greater than 100%.
My first thought was that the current measurement for the pulsed version must be incorrect - the pulsed supply current may not be registering correctly on the DMM. To test this, I added a current sense resistor in line with the battery, and monitored the drop across the resistor with an oscilloscope. There was initially a little droop during the pulse, so I added a 330 μF low-ESR aluminum polymer capacitor across the supply to further average the current, which removed the remaining ripple from the current draw. Across all these experiments, the average current remained 26.3 μA.
Instrumenting the Board
So, now we have to consider the efficiency of the pulsed circuit. My approach is to measure the LED current and voltage waveforms, calculate the integrated net electrical power delivered to the LED, and divide by the total supply power. I re-worked a V1.0 board to add a 1-ohm current sense resistor and integrated oscilloscope probes:

Here's the schematic for this re-worked board:
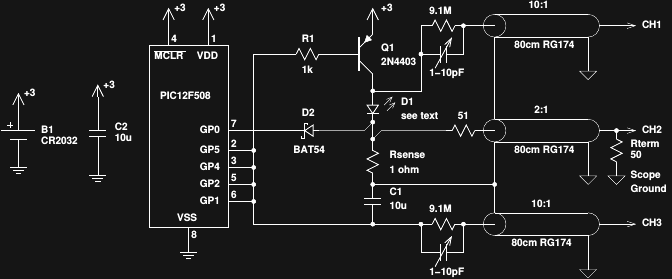
To measure the circuit without disturbing it too much, integrated "10x" probes were made for channels 1 and 3 (measuring the LED and capacitor voltage, respectively). The 9.1M resistors form a voltage divider with the scope's 1M input resistance, yielding a 9.9x probe. The trimmer capacitors were adjusted with the scope's compensation output before connection to the LED circuit. Since the voltage drop across the 1 ohm current sense resistor is so small, using a 10x probe would limit the accuracy of oscilloscope measurements. Luckily, the small resistor allows a simple "2x" Z0 probe to be used instead - in this case, a 51 ohm resistor is used in series with the signal, and a 50 ohm pass-through terminator is inserted at the scope end - yielding a 2.02x probe. I only had 5% resistors available at the moment, so the accuracy here isn't going to be stellar. I sacrificed some cheap RG174 BNC cables from ebay to make these probes. Note that the scope ground and circuit "ground" are at different potentials - "floating" the scope is easy for battery-powered circuits.
Here's what CH1 (LED voltage + Rsense drop) and CH2 (Rsense drop) look like. The integrated probes eliminate ringing artifacts:
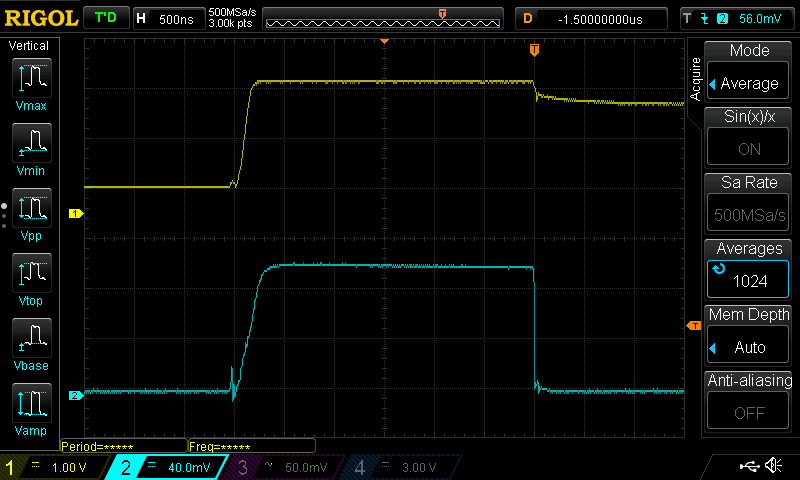 The pulse should be 3 μs long (subject to variations of the internal RC oscillator on the PIC12F508), and comes pretty close except for a brief ramp-up time. The LED current is around 102 mA for the pulse, and the forward voltage is 2.52 V. Estimating the pulse width to be 2.875 μs, this means the LED is receiving 7.39x10-7 joules per pulse. The pulse frequency is 45 Hz, resulting in a total power delivered to the LED of 33.3 μW. This circuit, as instrumented, draws 28.3 μA from its 3.0V supply, or 84.9 μW. The calculated electrical efficiency is then 33.3/84.9 = 39.2 %. This doesn't make any sense - how can this circuit, at 39.2 % efficiency, produce a much brighter output than the simpler one at 67.7 % ?
The pulse should be 3 μs long (subject to variations of the internal RC oscillator on the PIC12F508), and comes pretty close except for a brief ramp-up time. The LED current is around 102 mA for the pulse, and the forward voltage is 2.52 V. Estimating the pulse width to be 2.875 μs, this means the LED is receiving 7.39x10-7 joules per pulse. The pulse frequency is 45 Hz, resulting in a total power delivered to the LED of 33.3 μW. This circuit, as instrumented, draws 28.3 μA from its 3.0V supply, or 84.9 μW. The calculated electrical efficiency is then 33.3/84.9 = 39.2 %. This doesn't make any sense - how can this circuit, at 39.2 % efficiency, produce a much brighter output than the simpler one at 67.7 % ?
I did take a few minor liberties with this estimate, ignoring the fact that slightly incorrect resistor values were used in the probes and the increased loading of the 2x probe, and assuming a rectangular pulse shape. So, I downloaded the waveforms from the scope, applied correction factors for the nominal resistor values (I'm still ignoring the 5% resistor tolerances), and numerically integrated using the trapz() function in octave to find the total pulse power delivered to the LED. This integration yielded 7.384x10-7 joules per pulse, basically identical to the above estimate.
There could be something wrong with these measurements or calculations - if you notice something, please comment. Other than having made a gross error here, my current theory is that the LED itself is much less efficient at converting electrical power to light at very low currents. The typical efficiency curves for LEDs show them being more efficient at lower currents, but these curves don't usually extend down into the μA range.
These experiments have left me with two things I want to investigate. First, I can build a simple linear-response photometer with a photodiode and low bias-current op-amp and measure the LED efficiency both in the μA range, and the many-mA range. Second, I'd like to measure how much of the "extra" perceived brightness is due to the pulsed LED drive. Since this is a physiological effect, we have to use (a) human test subject(s) to evaluate relative brightnesses of the LEDs. I can build a Joly photometer for comparing the perceived brightness.
The other take-away from this result is that if the efficiency really is only 39.2 %, there's plenty of room for improving the pulsed circuit. You might even be able to double the runtime.
 Ted Yapo
Ted Yapo
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
Looking at the data sheet for that LED, the relative luminous flux at 100mA is somewhere around 0.3lm. They don't graph it lower than that, but the curve for the cyan LED would suggest a non-linear drop, possibly quite steep at some low current value. So your ~100mA pulse should be driving the LED to put out around 0.3lm per pulse. I'd be interested to see a 60fps video of this. Since your pulse frequency is 45Hz, the camera should pick up a flicker, plus the CCD isn't going to be susceptible to this http://techon.nikkeibp.co.jp/english/NEWS_EN/20080407/150114/
Are you sure? yes | no
I'm not sure what cameras I have available at the moment - I'll have to take a look.
Are you sure? yes | no
I found my Prosilica EC750, set it to 44 Hz (just slower than the flash rate), 1 ms exposures, and shot the DC and pulsed LEDs. This has a nice stroboscope effect to slow down the flashes:
Interestingly, the pulsed LED is glowing even between pulses - with what seems to be almost the same output as the DC LED. Of course, there can't be that much DC leakage current through the pulsed LED, otherwise there'd be nothing left for the pulse.
EDIT. This one shows it much better - and you can see a "sync line" pass through the pulsed LED while it's "off". The stop-motion isn't perfect .
Are you sure? yes | no
Very nice! This seems to show what I think we both expected: the RLF drops off drastically once you go under 100mA, and that combined with the physiological limitations of the human visual system, the pulsed LED appears much brighter, even though the electrical efficiency of the system may in fact be lower.
Are you sure? yes | no