Inverse Kinematics (IK) allows to find the robot's joint parameters (q1, q2, q3, q4, q5, q6) that do robot's tip to position according to a specific spatial location (p,[n,o,a]).
To do the Thor's IK calculus I have used the kinematic decoupling procedure. This procedure allows to calculate, the joint parameters (q1, q2, q3) that place the robot's tip in a point of the space first and then calculate the joint parameters (q4, q5, q6) responsible for the wrist's position and orientation.
Geometric method: q1, q2, q3
We have to bear in mind that the point that the IK will position won't be the Tool Center Point (TCP) but the 5th joint axis' center (Pm). Therefore, given an orientation and position of the TCP (noap_tcp) and because the 4th, 5th and 6th joints cross in a single point and the TCP's Z axis crosses Pm, then:
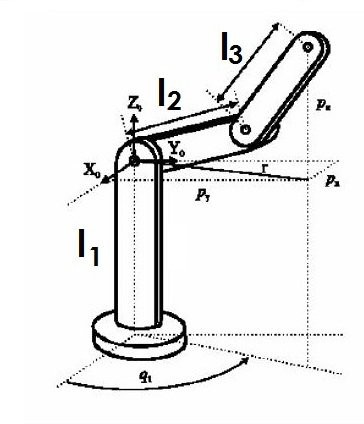
Geometrically we obtain the following equations:
where:
Rotation matrices: q4, q5, q6
Thanks to the forward kinematics the Pm's position and orientation due to q1, q2 and 13 can be obtained. As the position is no longer needed, it can be possible to operate only with the R:
Which is the same as:
I have used the SymPy tool (mentioned on the Forward Kinematics log) to do the symbolic calculus. The results are the following:
Hope you like it!
 AngelLM
AngelLM
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
unfortunately the results are not shown anymore. It says "Invalid Equalation".
Same problem in Forward Kinematics log.
Are you sure? yes | no
Maybe this is a late reply, but I just updated the log and fixed the equations
Are you sure? yes | no
Hello AngelLM, what is the SymPy code used?.
Are you sure? yes | no