This is the second iteration of a geodesic ice dome, the first version was Ice Station Thuban.
The spherical photograph is actually the eye of a krill.
http://en.wikipedia.org/wiki/File:Krilleyekils.jpg
It's analogous to what is going on with the Thuban Prime dome, and as you can see, makes a pretty good sphere, with small units of mostly hexagonal shape.
If you use an icosahedron as your basis, twenty equal triangles can be projected onto a sphere. An icosahedron is a pretty poor approximation of a sphere, which is why Ice Station Thuban used a rhombic triacontahedron as its basis, which is a bit better. However, an icosahedron has the benefit of having very few vertices (twelve) per sphere, and this is actually a benefit for a very practical reason.
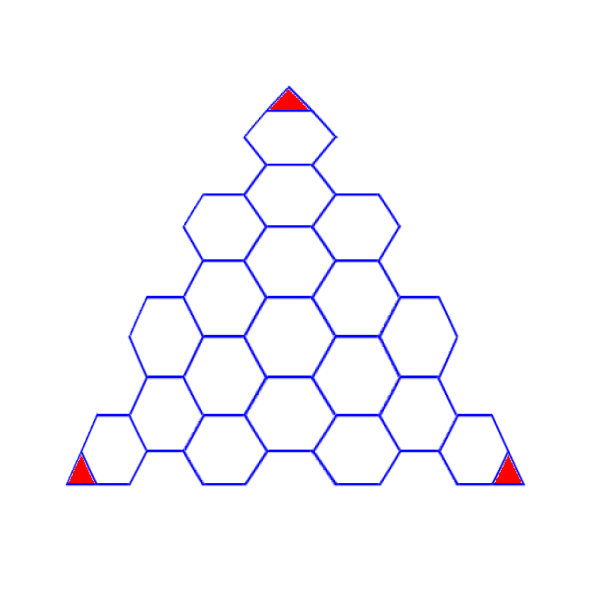
Consider the triangle of the icosahedron. If you were to subdivide it as per the following diagram, you would get a hexagon in the middle, and the triangles in red would join with the triangles from the adjacent icosahedral faces, to form pentagons. The result would be a polyhedron with twelve pentagons and twenty hexagons. This composite polyhedron approximates a sphere more closely than an icosahedron - in fact, this pattern is quite similar to the very familiar Telstar soccer ball (proportions slightly different).
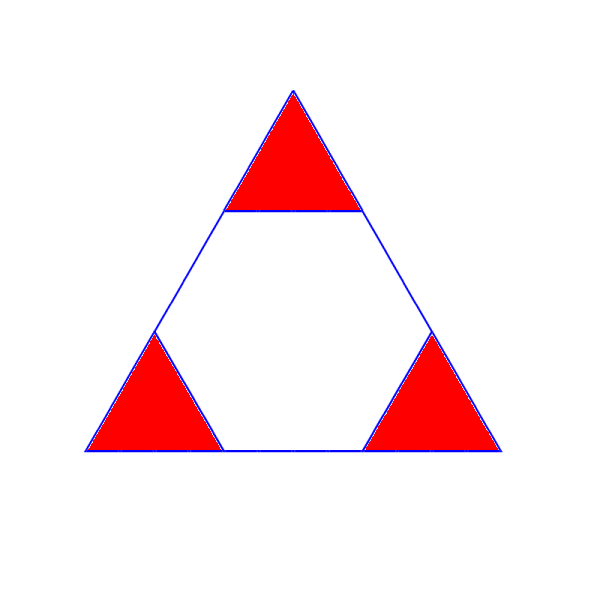
If you decided to double the linear precision, and instead of dividing the icosahedral edge into three, you mensurated by six, you could tessellate the triangle as per the following diagram:
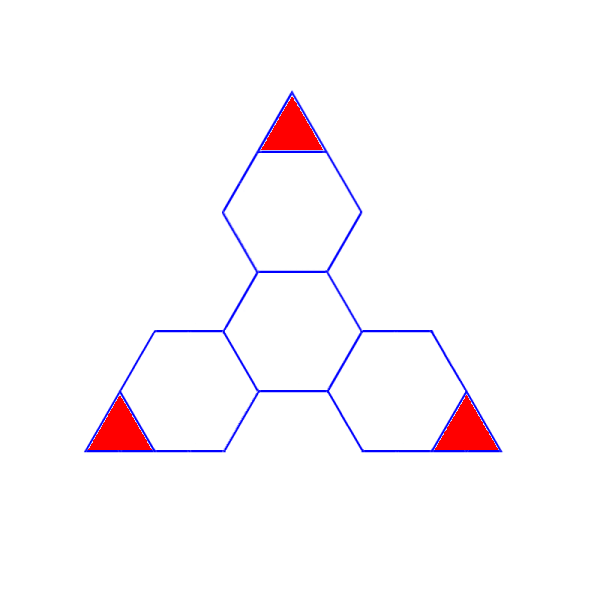
As you can see, you will now have five and a half hexagons per icosahedral face, instead of only one. But you still only have three red triangles, which form the twelve pentagons. A projected sphere will now have 110 hexagons, and this will be much more spherical than an icosahedron. All hexagons are not quite the same, they are distorted once you project the vertices on to a sphere, as per the following diagram, which is a bit exaggerated for illustration (and somewhat poorly - the red triangles really should all be equivalently proportioned).
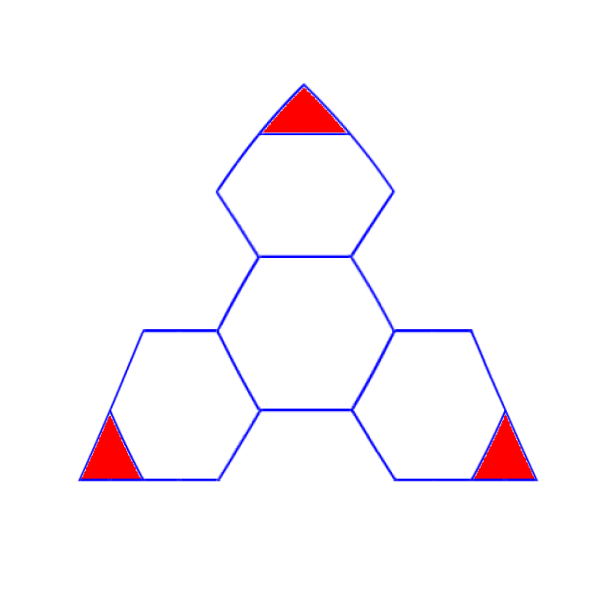
For a dome, to do this precisely, you would now have to create a lot of different, uniquely shaped forms, We don’t want to do that. (Or at least I don’t want to - that is not an optimized procedure, it is labor intensive and highly susceptible to derailment due to practical concerns. With Ice Station Thuban, I had only four unique shapes, and it was more than enough. Too much, really.)
But let’s go further. In the following diagram the icosahedral edge has been mensurated by twelve (double again!), leading to a tessellation that has 23.5 hexagons per face.
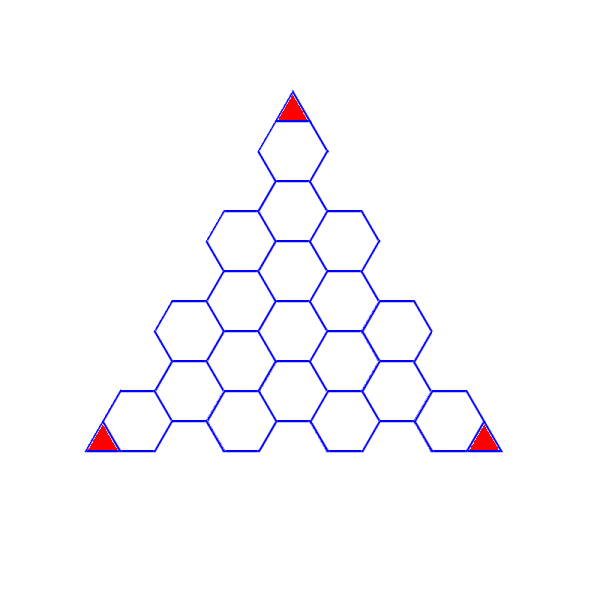
This will give you an approximate sphere with 470 hexagons… and still only 12 pentagons. Projected onto a sphere, the hexagons will still be very different, a lot of unique shapes.
The thing is, if you continue this process, you will get more and more tiny hexagons, and exactly twelve pentagons every time. At a certain point, the size of the hexagon is within your manufacturing tolerance. This effectively makes all the hexagons statistically “the same” - plus or minus.
This is what you see in the krill eye. Nature has a certain amount of time to grow these units, so they are all going to be just about the same size. But in order to make a sphere, they will jam together and naturally from hexagons (primarily) - except for some number of dislocations to correct for sphericity. If nature did things exactly repeatably, there would need to be twelve pentagons to account for the dislocations. (Note I did not say perfectly, because nature is the gold standard of perfection - perfection does not necessarily mean repeatable. It means robust, optimized for production quality per energy usage.) In the krill eye, you can see a handful of dislocations. They are not perfect pentagons, but I am guessing, if you average all krill eyes ever to have existed, there will be pretty close to twelve per idealized full-sphere eye. (Obviously an eye is not an entire sphere, it...
Read more » Kenji Larsen
Kenji Larsen



 Darrell Johnson
Darrell Johnson

 w_k_fay
w_k_fay
 julio perez
julio perez
Thanks for the explanation. Very interesting