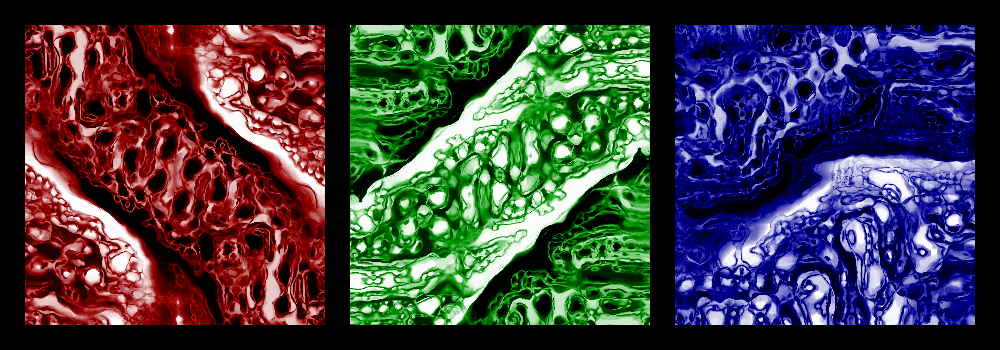
Turing patterns are a mathematical model for natural patterns such as stripes and spots. The model explains how these patterns can emerge from random initial conditions thanks to the interaction of two substances, called activator and inhibitor in the following. Jonathan McCabe published an article describing an algorithm to generate more complex Turing patterns using several layers, or scales, of activator/inhibitor couples. Very useful implementation details were given later on Softology's blog.
Conceptually, the idea is similar to that of Conway's Game of Life: create an image with random pixel values, then repeatedly apply some simple rule on each pixel that changes its value based on the value of its neighbors. If the rule is chosen wisely, interesting and unexpected patterns emerge.
This project is a C++ implementation of a multi-scale Turing patterns generator based on McCabe's algorithm. As the algorithm requires updating each pixel individually, and this update gets more computationally expensive whith each additional scale, my goal is to make the implementation quite efficient. I am also more interested in generating videos than static images, which is why the project uses libav/FFmpeg. Finally, I want to understand how the different parameters of the algorithm (e.g. activator, inhibitor, number of scales) influence the generated patterns, and explore the creative possibilities given by symmetries and color palettes.
 xD
xD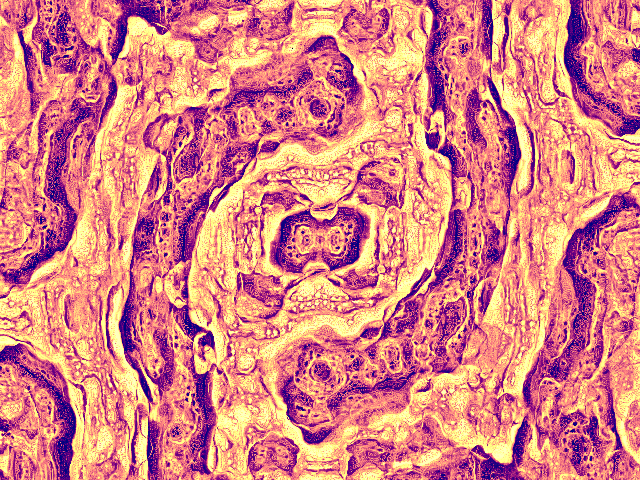 The improvements that I'm most interested in are the following:
The improvements that I'm most interested in are the following: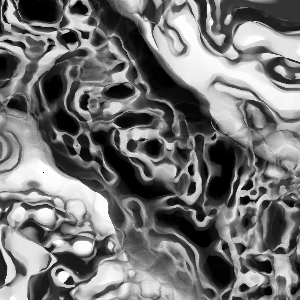 Everything's fine. Now let's try with 400x300:
Everything's fine. Now let's try with 400x300: Wooow that's a mess. There seems to be stuff repeating and overlapping... Hard to understand what's happening. But with a small difference between the width and height, we can see a bit clearer. The picture below on the left is 301x300, the right one 302x300.
Wooow that's a mess. There seems to be stuff repeating and overlapping... Hard to understand what's happening. But with a small difference between the width and height, we can see a bit clearer. The picture below on the left is 301x300, the right one 302x300.
 Turns out an image 301x300 gets split in two zones, 302x300 in three zones, 303x300 in four zones... For 400x300, there are so many zones that it's hard to recognize anything.
Turns out an image 301x300 gets split in two zones, 302x300 in three zones, 303x300 in four zones... For 400x300, there are so many zones that it's hard to recognize anything.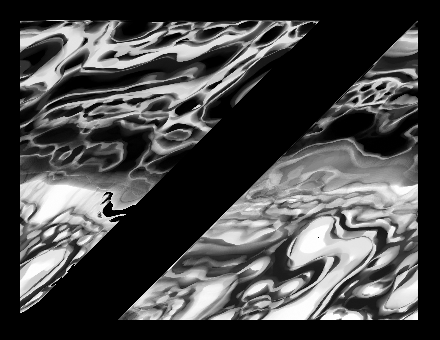 Put the right zone to the left and vice-versa:
Put the right zone to the left and vice-versa: See where this is going? Now apply some shear to de-distort the picture:
See where this is going? Now apply some shear to de-distort the picture: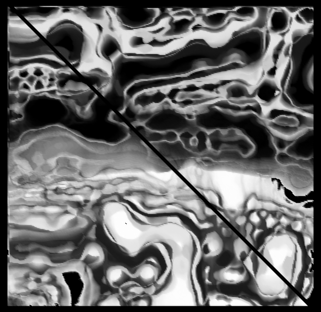 The zones are not independent, it's only one picture but distorted and somehow split and wrapped around. Or is it some kind of aliasing? I still don't know what's happening there, but hopefully I'm getting closer.
The zones are not independent, it's only one picture but distorted and somehow split and wrapped around. Or is it some kind of aliasing? I still don't know what's happening there, but hopefully I'm getting closer.



 Andy Oliver
Andy Oliver
 Christian Walther
Christian Walther