Why another clock?
The clocks people use to tell the time of day consist of a display to show what time it is, a timebase to drive the display, and a case to hold them. The number of ways people have found to build clocks -- to vary the display, the timebase and the case -- is truly astonishing. Sadly, since the development of the super-cheap, accurate quartz clock movement almost all of the interesting new clocks use that as their timebase and only vary the case and the display.
There are exceptions, of course. Some interesting new clocks use traditional mechanical movements such as pendulums or balance wheels. Others use the 50 or 60 Hz of the AC power as their timebase. A few use standard time signals such as those from WWV, time.nist.gov or the GPS constellation to keep their primary timebase synchronized closely with Coordinated Universal Time. But for the most part, hobbyist clock builds and commercial clocks for consumer use all employ a quartz movement and differ from one another just in their the case and display.
For commercially made clocks the reason is obvious, but why do our clock builds go down this same path so often? Personally, I find the timebase part of a time-of-day clock just as fascinating as the case and the display. Maybe more so. I guess that’s what motivated my bendulum clock build.
The fun and success I had with that build led me to think about other ways I might make a timebase for a clock. In the course of that build I struggled for quite a while with the fact that its bendulum, like all physically oscillating timebases, from pendulums to quartz crystals, changes its rate slightly as the temperature changes. Whenever something physical oscillates back and forth, thermal expansion tends to change the rate at which it does so. To counteract this, you can either compensate for it by observing how it changes and counteracting it in the design (the approach I took with the bendulum) or try to hold the temperature constant (as is done with an “oven controlled crystal oscillator” or OCXO). But is there another approach all together?
How is this one different?
After having the question roll around in my head for quite a while, one day a possible answer just sort of arrived out of nowhere: radioactive decay.
The average number of decay events that occur in a sample of a long-lived radioisotope changes very slowly over time and in a way that is completely predictable. Importantly, the rate of decay doesn’t change at all with changes in temperature, pressure or other environmental conditions. What I started to think about was whether I could derive, say, a 1Hz timebase from the radioactive decay of a small, safe sample of some long-lived radioactive substance.
The problem is that although the rate of decay is completely predictable over the long haul, every decay event is completely random in time. A sample small enough to be both obtainable and safe will necessarily have a number of decay events per second that’s pretty small. That means the number of decay events that occur in any given second will be unpredictable.
Suppose you had a sample you knew underwent 10 decay events per second, on average. If you drove a clock by counting decay events, moving the second hand ahead by one each time you got to a multiple of ten, the clock would keep time. On average. But in the short term it would always be wrong. Sometimes the clock’s “seconds” would occur quickly and sometimes there would be long pauses between them. If you’ve ever heard a Geiger counter you know how irregularly the clicks come. I don’t see any way to directly derive a regular timebase out of that.
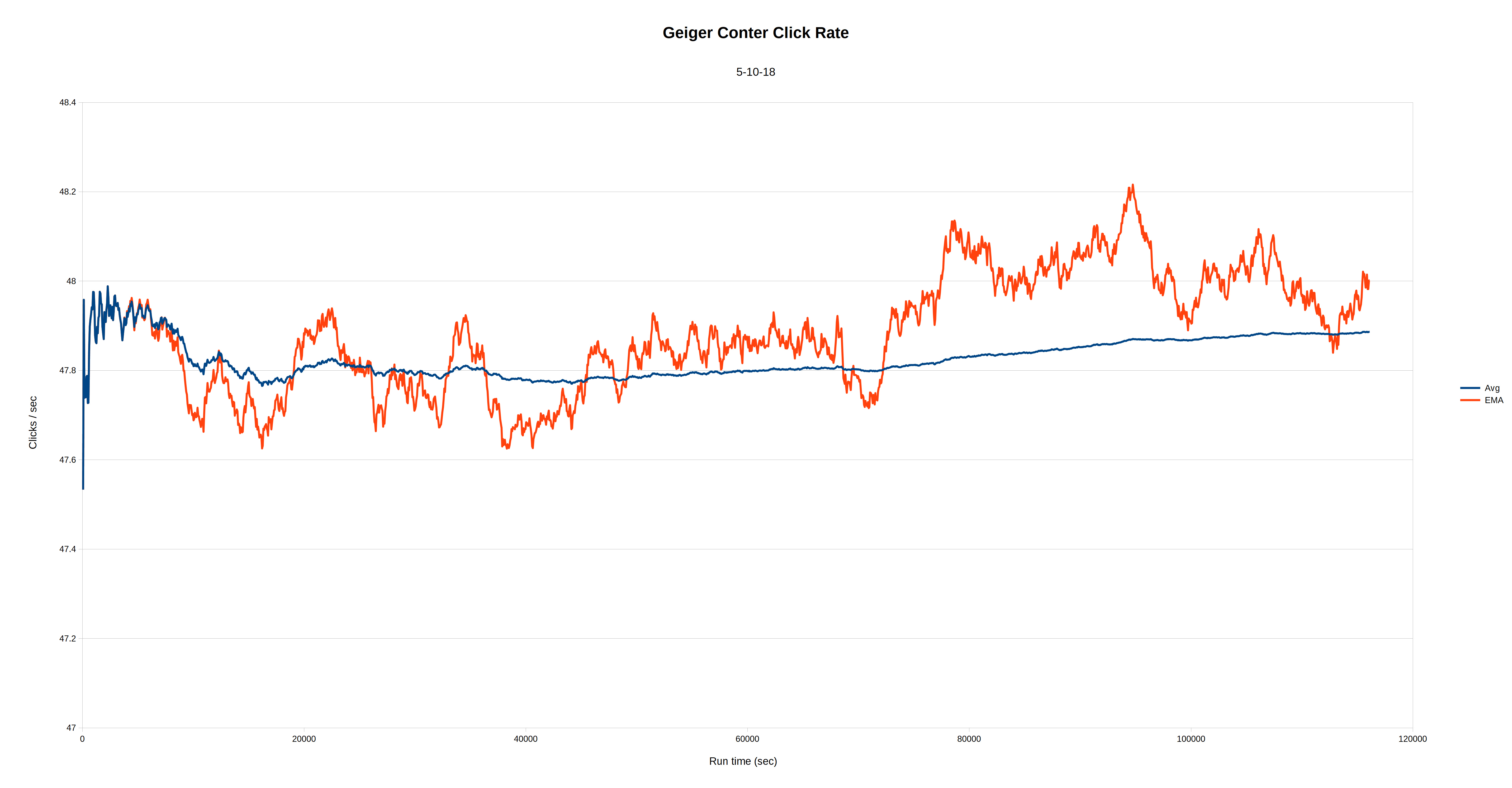
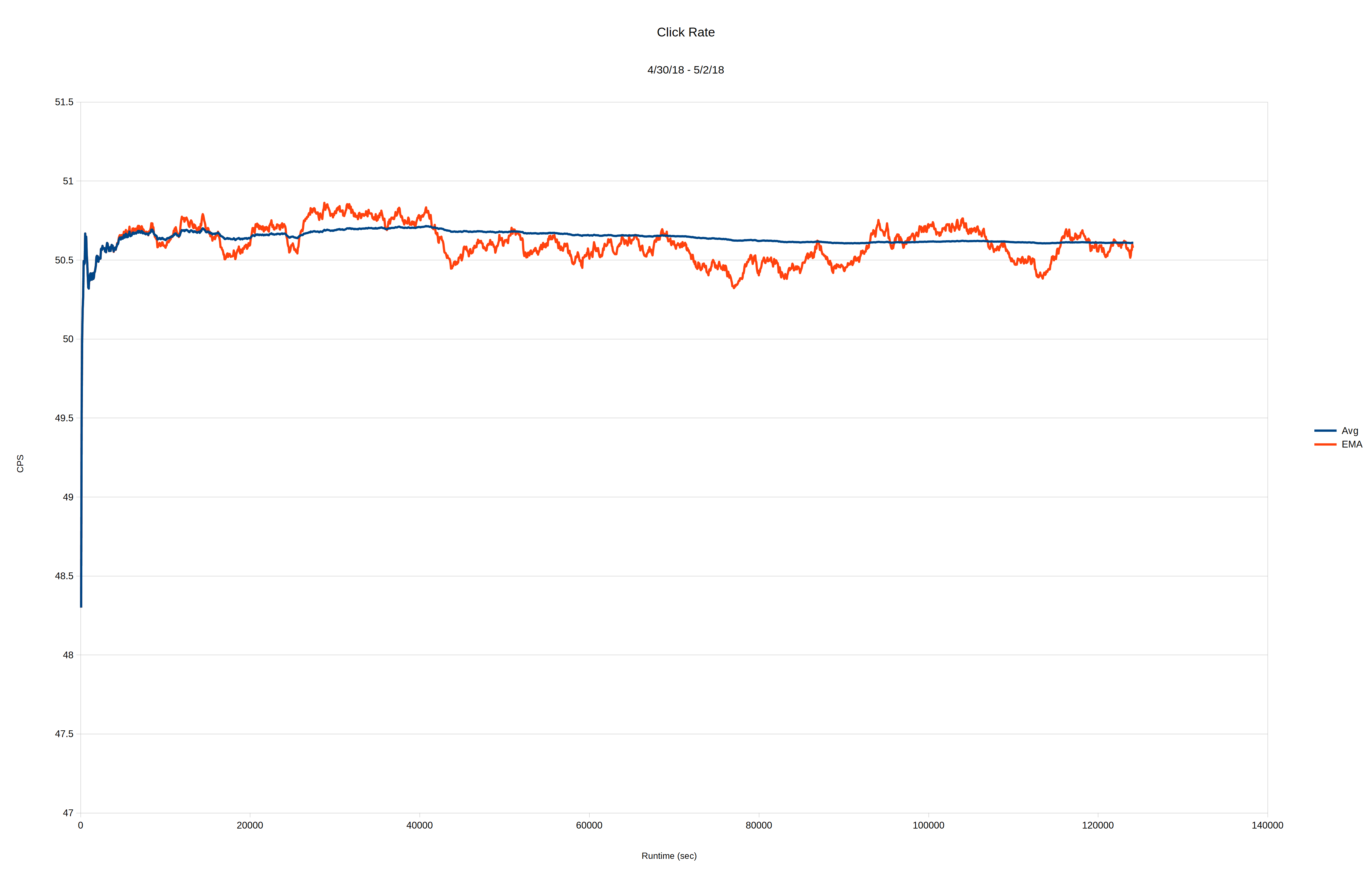
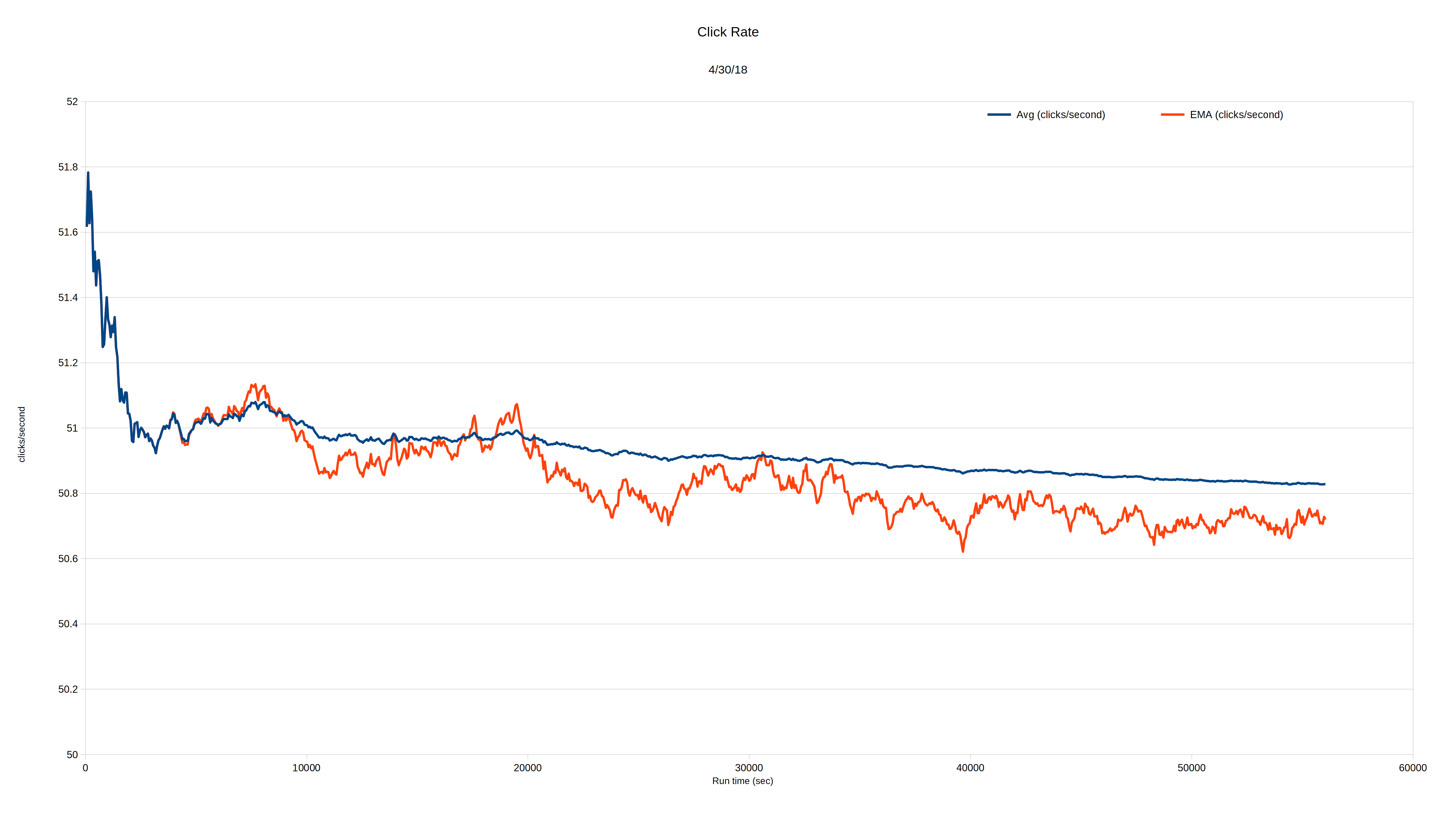
But the fact that the average decay occurs so predictably means that we should be able to use such a radioactive sample to adjust the run rate of a not-so-good 1Hz timebase so that it stays very close to correct and over...
Read more » Dave Ehnebuske
Dave Ehnebuske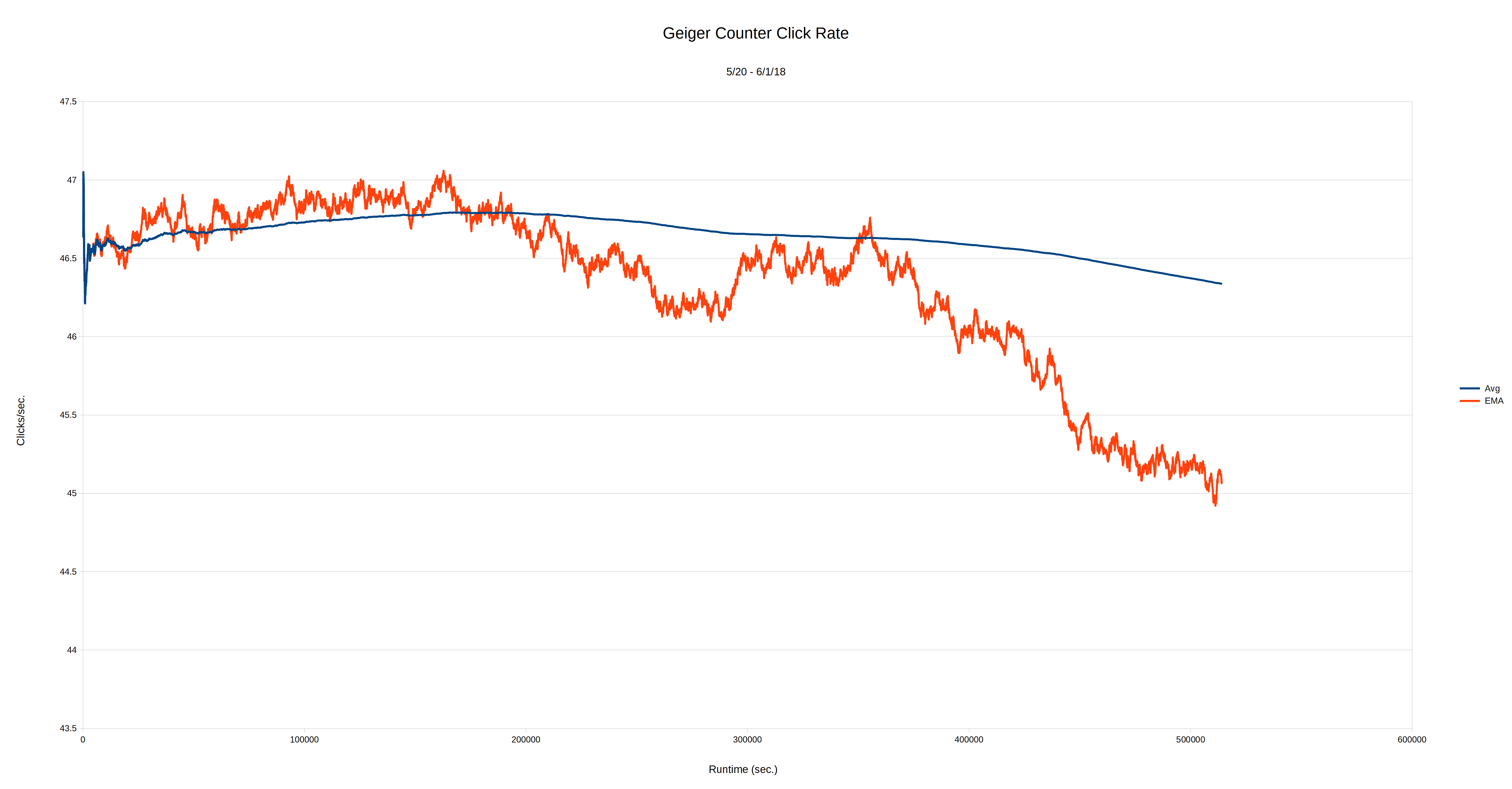




 Simon
Simon
 Kn/vD
Kn/vD
 jens.andree
jens.andree
As I see it, the approach has something in common with a mechanical clock:
* the exposure of the detector to the source must be constant (angle, offset)
* in the case of alpha particles properties of the air must be constant (better: no air at all)
* the sensitivity of the detector threshold must not depend on temperature, voltage, aging, etc.
In other words: any variation in parameters that change the sensitivity of the setup needs to managed.