This project is going to happen in the build logs: I'm basically treating this as a blog for ongoing experiments with the FL2k dongles. This is a spin-off from #AM Band Voice Frequency Marker where I initially used this device to implement a project that had stalled for about a year.
For background information and the code you need to operate these dongles as general-purpose DACs, see the osmocom.org wiki page. The short story is that there's a way to turn off the horizontal and vertical blanking interval on these inexpensive USB3.0 adapters so they can blast out 8-bit analog values at 100 MSPS or more on three channels.
Feedback or suggestions on these ideas are welcomed, as are collaborators.
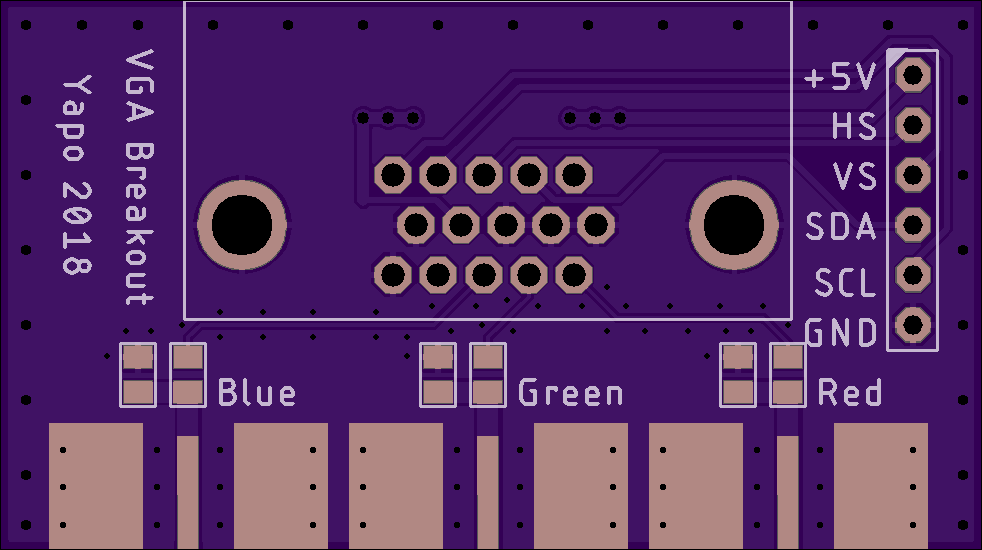
For anyone wishing to start experimenting with these dongles, I've designed a breakout board that brings the red, green, and blue channels out to SMA jacks and matches the 75-ohm output of the VGA to 50-ohms. You can order the PCB from OSH Park.
So far, I've decided I want to explore the following things:
ZOH Limitations
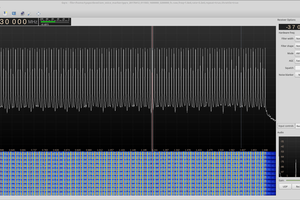
Overcoming the zero-order-hold (ZOH) limitations on higher-order Nyquist zones. The DACs in the FL2k don't have any explicit filtering, which is ideal for VGA output, and also allows you to generate RF outputs at higher frequencies than would otherwise be implied by the ~100 MSPS data rate. But, there's an implicit "filter" in the DACs themselves: the zero-order-hold function, in other words, the fact that the DAC maintains a constant value during each sample time. This has the effect of filtering the higher-order Nyquist zones with a sinc-shaped envelope. In the plot below, you can see how the higher-order zones drop off precipitously up to 1.5 GHz. The yellow curve is the envelope of the FL2k output, and the magenta the noise floor of the analyzer. If you want to generate 1.5 GHz signals with this device, you are really fighting a lot of loss.
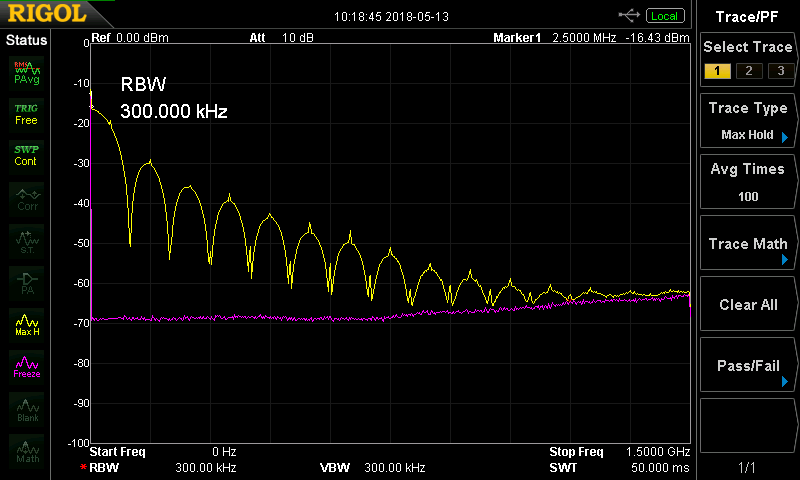
(Aside: to gather this envelope data, I generated a chirp signal from DC to 50 MHz, and output it at 100 MSPS. I set the analyzer trace to "Max Hold," and let the envelope gradually fill-in while the chirp swept through the frequency range.)
Of course, you can change where the zeros are in this output by changing the sampling frequency, but the envelope is still limiting. Ideally, instead of a zero-order-hold, the DAC would output infinitely narrow delta functions for each sample - this would produce un-attenuated harmonics for all Nyquist zones. Commercial direct-sampling RF DACs approach this ideal by shaping the DAC's impulse response. For example, Maxim's MAX5879 has four different selectable impulse responses (hint: read the linked page for much more info on the subject) that allow different envelopes to be created. One of the responses is equal to the ZOH, a second returns the output to zero for half the sample period (more closely approximating a delta function), a third response inverts the DAC output half-way through the sample period, while a fourth combines the two, using true and inverted outputs for one quarter of the period each. The article describes the resulting envelopes, which show less attenuation than the simple ZOH.
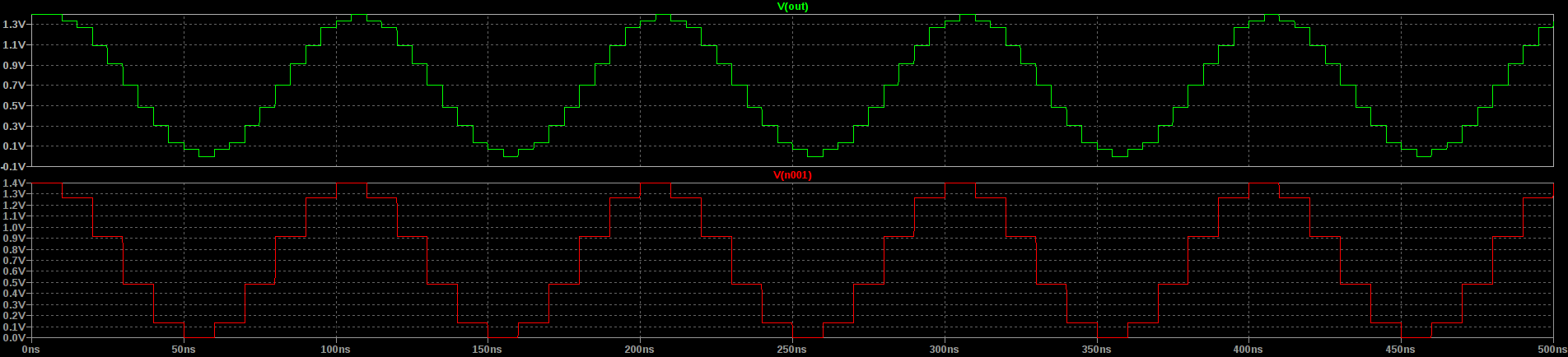
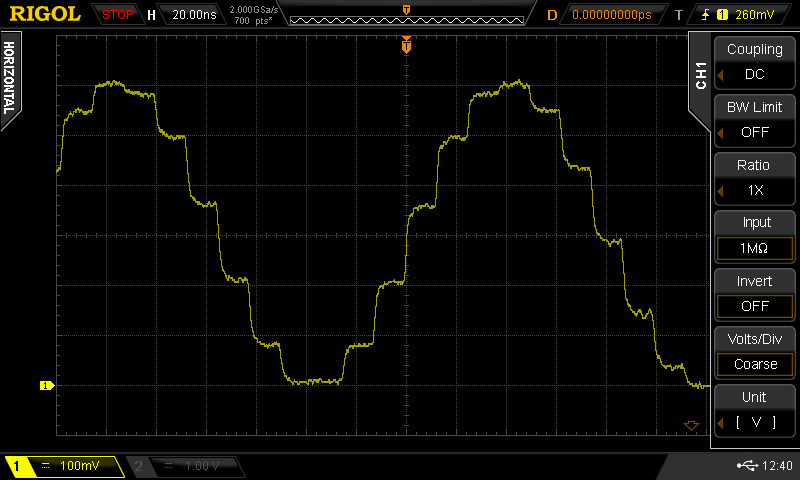
You can see the evidence of the ZOH in the time domain, too. Here's a 10 MHz sine wave sampled at 100 MSPS through the FL2k:
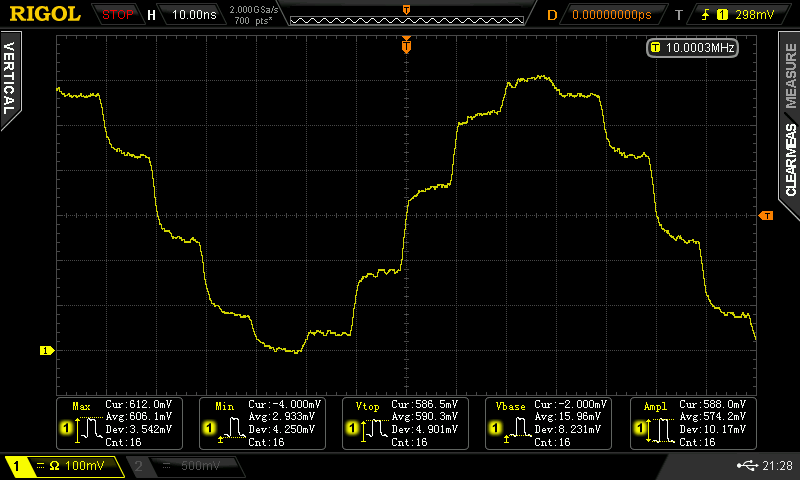
You can see the 10ns steps clearly. The settling time for these large steps isn't great, but that could also be from a number of other factors, including the test setup.
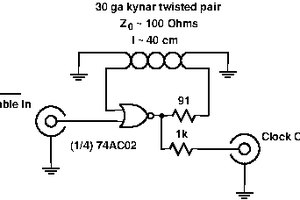
How to improve this? The idea would be to generate a fast sample of the DAC output. For example, one could use a diode sampling gate, or maybe even just use a diode to shunt the output to ground for some (or most) of each sampling period. To drive the sampler, you'd create a short pulse based on output from either the green or blue channel (see below...
Read more » Ted Yapo
Ted Yapo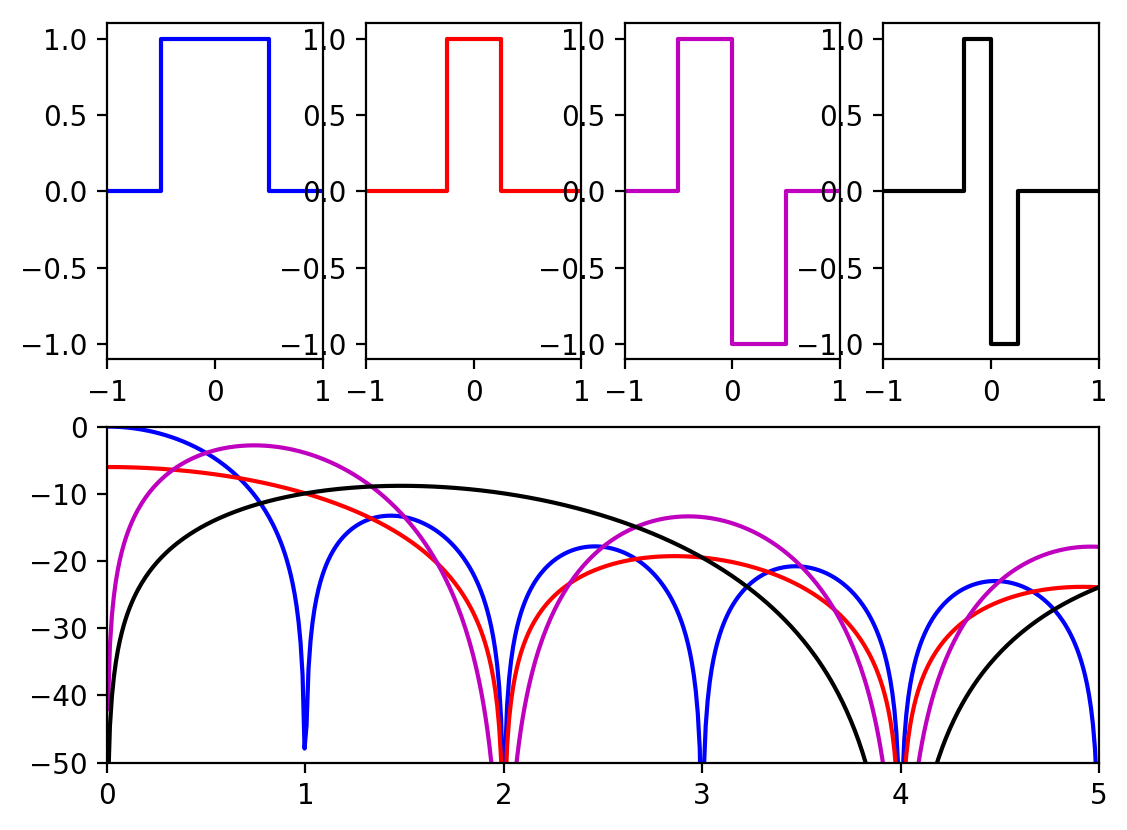







 Andrew Ferguson
Andrew Ferguson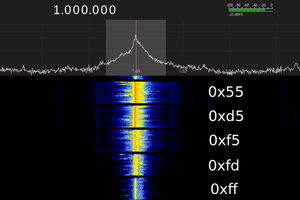
"It's kind of like doubling the sample rate"
- It looks like you're doubling the number of steps, ie increasing the resolution. i believe that's the equivalent of adding 1 bit of resolution.