Hello All!
In this post I am hoping to showcase some of the design work that goes into motor selection. If you are curious about this process, I highly recommend the free resources available at the California Mechatronics Center .
This company is actually run by one of my previous university professors and the workflow presented SERIOUSLY cuts down on a lot of mechanical design iteration. The documentation shown here could certainly help you build much more precise CNC/servo systems than I present here (although beam deflection seems to be missing...).
After all was said and done, this process seemed to work out fairly well considering all of the parts are DIY robotics components. It met all of our requirements on the first go!
I did, however, make one glaring mistake:
After assembly and testing, the motors could stop so quickly that robot would flip over! Pretty much a catastrophe an industrial scale, but not a big deal with low-mass system such as this. Certainly something to take into account in the future. Rather than programming in a maximum de-acceleration rate, a small counterweight remedied the problem.
So lets dive into it!
The primary issue in selecting a motor is ensuring that the motor can meet both of your torque and speed requirements. If you have these specifications before you start, the worst is over! If not, you will have to estimate them yourself.
Here is the big boy check list. Seriously, this process separates the engineers from the hobbyists.
The first step involves in creating a motion profile for each of your motors. The key here is to find your systems top speed and the amount of time you are allowed for the motors to spin up. This will help you determine the motors required angular acceleration. See below
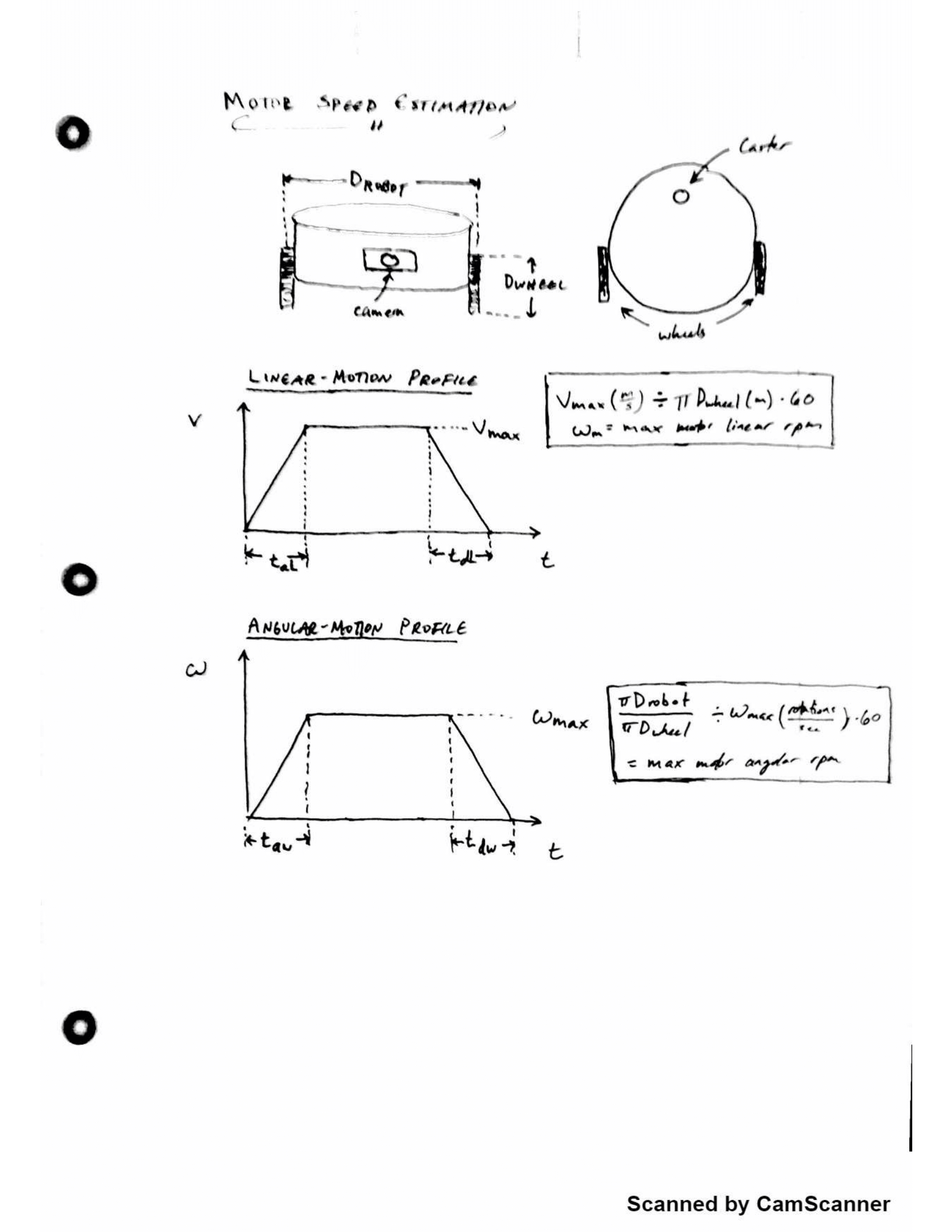
Notice that we have created two motion profiles. One helps determine the acceleration required to meet our requirement for the bots linear motion (i.e. forwards and backwards movement), and the other to determine the acceleration to meet the requirements for the bots turning speed (i.e. spinning about its center).
The big design take away from both these graphs (for our project anyway): the relationship between wheel sizes, robot diameter and the maximum required motor velocity.
A smaller diameter robot really cuts down on the acceleration required for turning, and larger wheels will likewise cut down the acceleration required for linear velocity.
Now that we have our head around that, lets take a look at our kinematics, and calculate our peak torque:

Luckily for me, this system is a simple one:
- There are no major safety hazards if one of the motors fails.
- There are no mechanics (belts, ballscrews) to complicate our calculations -our motor go to a gearbox, and then wheels. These add extra inertia loads and frictional forces to account for.
- Our system is stable even if the motors are not running.
- No shear force on the motor shafts outside the weight of the bot.
So we don't really have to consider much in the way of frictional, gravitational, or thrusting forces.
Pretty easy living! All we have to really determine is the inertia the bot imposes on the motors, which can be treated as tangent load on the edge of each wheel (see the equation for Jrobot).
Tthe main thing to notice is that increasing wheel diameter is not without its drawbacks. While this does decrease the maximum required speed of the motor, it seems to add quite a bit more inertia (notice the inertia exerted by the bot increases with the square of the wheel radius).
So all that is left is to accurately estimate all of our equation parameters. I use matlab, but this could easily be excel. This will let you tweak each of your design parameters (in our case, bot diameter and wheel diameter). Lets plot all of our motor parameters as they vary with our bot dimensions.
Here is the output of our matlab script:
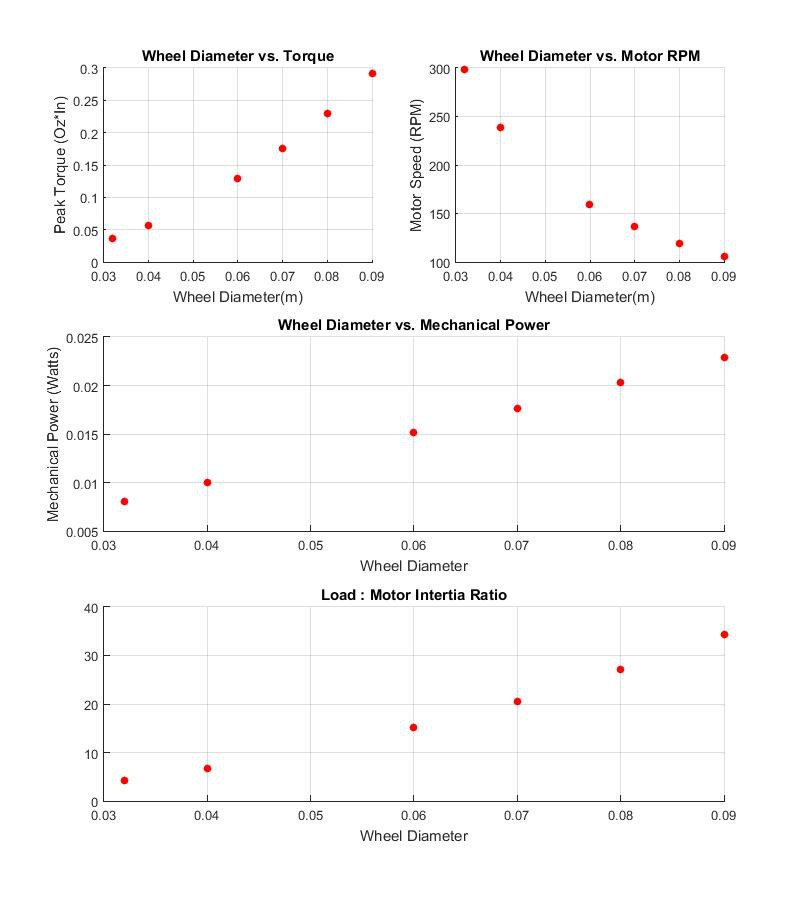
One parameter that is commonly overlooked is the ratio between motor inertia and load inertia. A lot of discussion here. The rule of thumb in the industry is to never exceed 50:1, but if your a controls whiz you can probably get away with much worse.
One last note, you really don't want to operate exactly at your motors maximum power output. You want your requirements to fall underneath the motors torque-speed curve.
Motor shopping and driver selection to follow!
Here is the matlab script:
Vbot = .5; % Top linear-speed (m/s)
Abot = 2; % Minimum linear-acceleration (m/s^2)
Mrobot = .90; % Mass of robot in Kg
Drobot = 0.15; % Distance between wheels in M
%Wheel options
Dwheel = [.032, .04, .06, .07, .08, .09];
Rwheel = Dwheel/2;
Mwheel = [.0032, .0043, .0114, 0.0141, 0.0198, 0.02267];
%Time to accelerate to Vbot
Ta = Vbot/Abot;
%Top speed of the motor in rpm
Wmotor = Vbot./(pi*Dwheel)*60;
%Inertial Loads
Jwheel = 0.33*Mwheel.*(Rwheel.^2);
Jrobot = 0.5*Mrobot.*Rwheel.^2;
Jload = Jwheel + Jrobot;
%Peak torque
Tpeak = Abot*(Jwheel + Jrobot);
%Calculating Power required:
Mpower = 2*pi*Tpeak.*Wmotor/60;
%Calculating Load:Rotor Inertia Ratio:
Jrotor = 10; %g*cm^2
Gratio = 30; %Gear ratio
Jrotor = Jrotor * 10^-7;
fig = figure;
set(fig, 'Position', [300 100 800 900]);
subplot(3,2,1);
scatter(Dwheel, Tpeak*141.611,'filled','r');
ylabel('Peak Torque (Oz*In)');
xlabel('Wheel Diameter(m)');
title('Wheel Diameter vs. Torque')
grid on;
subplot(3,2,2);
scatter(Dwheel, Wmotor, 'filled','r');
title('Wheel Diameter vs. Motor RPM');
xlabel('Wheel Diameter(m)');
ylabel('Motor Speed (RPM)');
grid on;
subplot(3,2,[3 4]);
scatter(Dwheel, Mpower,'filled', 'r')
title('Wheel Diameter vs. Mechanical Power');
xlabel('Wheel Diameter');
ylabel('Mechanical Power (Watts)');
grid on;
subplot(3,2,[5 6]);
scatter(Dwheel,(Jload/Jrotor)/Gratio,'filled','r');
title('Load : Motor Intertia Ratio');
xlabel('Wheel Diameter');
grid on;
 Brett Smith
Brett Smith
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.