Due the equations presented for the Position and Orientation Acquisition System has some issues, I decided to figure out why it happens and try to solve it. The clues are:
- I modeled the equation from Denavit-Hartenberg parameters through MatLab, and when I use the forward kinematics functions for the model it works perfectly.
- When the equations are tested in the real system a dependence between the axes appears, nevertheless it "try" to move as expected
It can be generated by two possible mistakes:
- The modeling is wrong formulated in some part .
- The device is wrong calibrated.
I tried to recalibrate and formulate variations of the model several times, but nothing works, so I just make another representation of the model by vector instead of Homogeneous matrix representation. The position of the end effector and its orientation are analyzed independently, the model is:
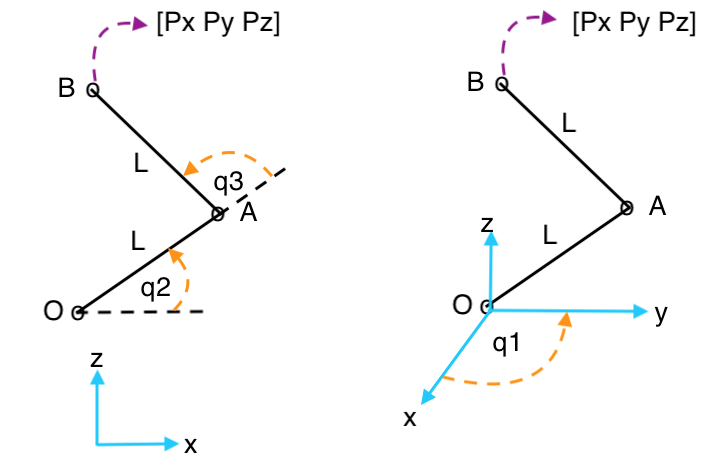
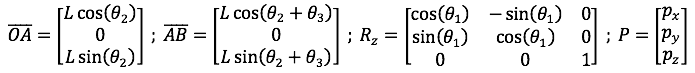
where:
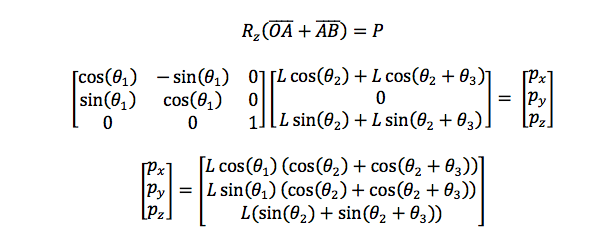
[Px Py Pz] is the end effector's position. The orientation is presented as the homogeneous transform form, so:

Where Rx, Ry and Rz are the canonical rotation matrix in each axis. To represent it as Euler angles (r,p,y) we need to make relations between the elements of the rotation matrix R, so:
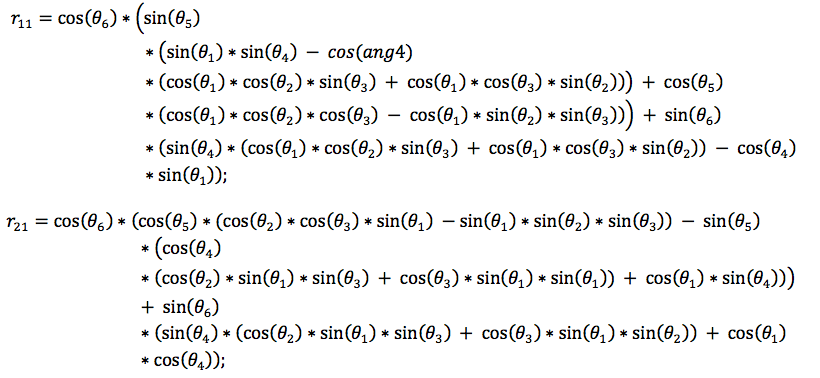
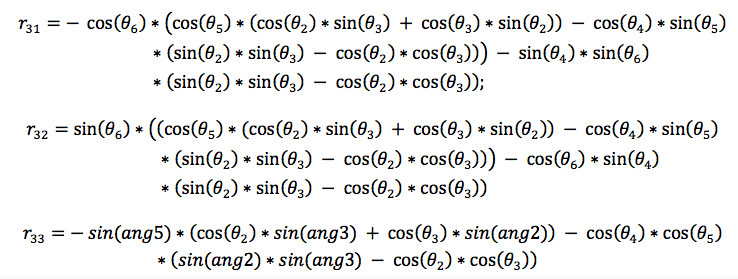
The Euler angles are:
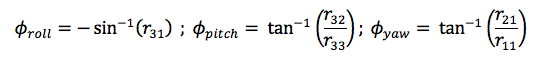
This is tested in a virtual environment in Unity (just move a cube) as the next vídeo show:
 Maximiliano Rojas
Maximiliano Rojas
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.