So far so good? Maybe! But how can you practically measure the current in the LED to demonstrate the ripple reduction?
I don't have a current probe for my scope and neither I can afford it. Secondly, measuring in a conventional way required a sense resistor, which would alter the results, and I should manipulate too much the already delicate measurements to compensate this effect and get the correct result.
KISS my LED
I opted for Keeping It Super Simple, you Stupid (this acronym is always different each time a read it). Here the setup, which I was staring at with sun-glasses, hopeless, trying to find a solution.

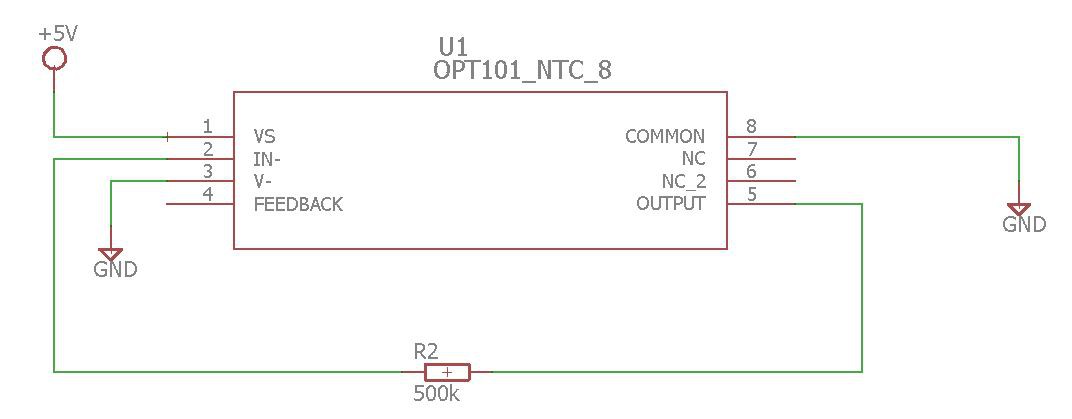
Then I realized that I had an OPT101 somewhere. I still can measure the light. But this is a somehow slow sensor. From the previous log, with my setup with a single LuxeonRebel LED, I had an operating frequency somewhere 300 kHz. Different supply and analog dimming will affect this, since it does not have any oscillation: is just the speed of the inductor to reach the thresholds!
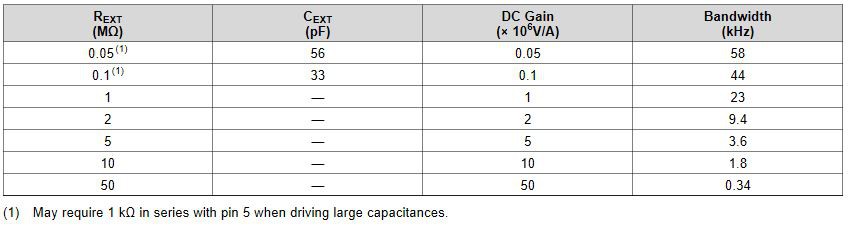
The OPT101 was used with external programmed gain:
With a useful table shown here:
 Here I don't care about the quantitative ripple reduction in absolute way, but more in a relative manner with respect to the solution with no ripple attenuation.
Here I don't care about the quantitative ripple reduction in absolute way, but more in a relative manner with respect to the solution with no ripple attenuation.
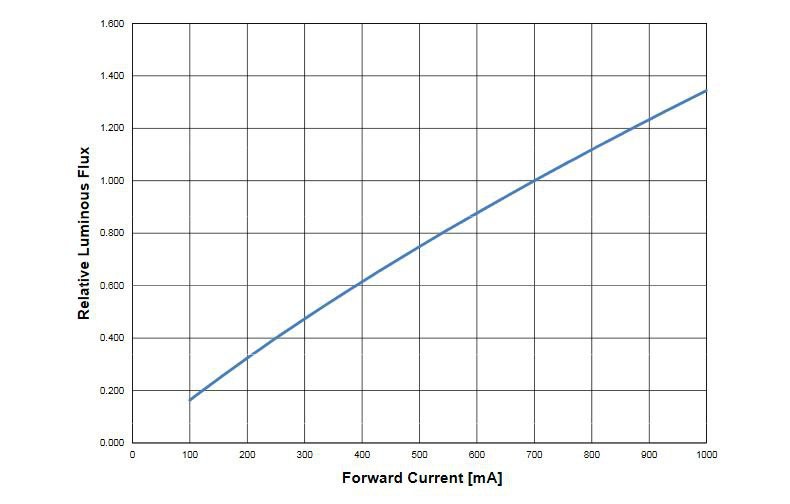
One last thing was to be sure that the LED could provide sensible light variation w.r.t. current variation. In my case, the operating point of the LED was somewhere near 400mA. The LED was a LXW8-PW40, with the following characteristics:
Finally some measurements
The results are showing an output from the photosensor of 35 mVp-p which is amplified by 500k times.
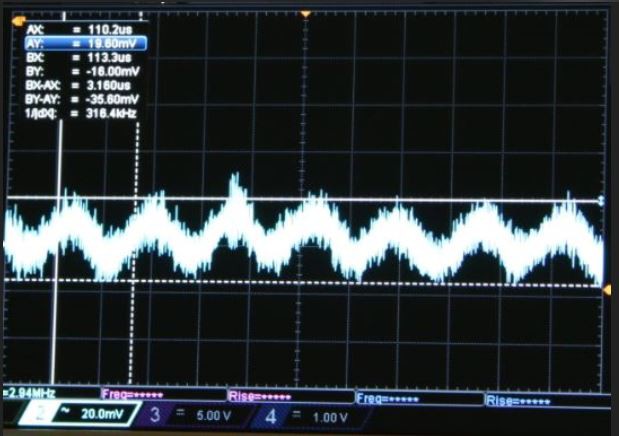
This is my reference point. Here with 300 Ω of sense resistor, reference voltage of 116 mV, results in a Iset = 386 mA. If the regulator provides +/-15% of ripple current, then 35 mVp-p will corresponds to the 32% of ripple measured in the previous log, where in current is 150 mAp-p. Applying 2.2 uF reduces this to 25 mVp-p.
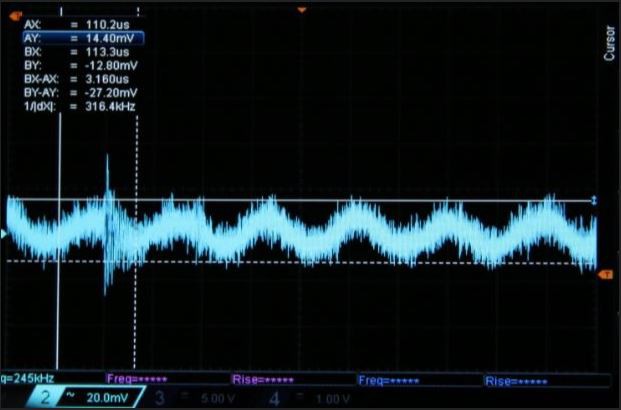
With 6.6 uF this reduces down to a value between 11 mVp-p and 13 mVp-p.
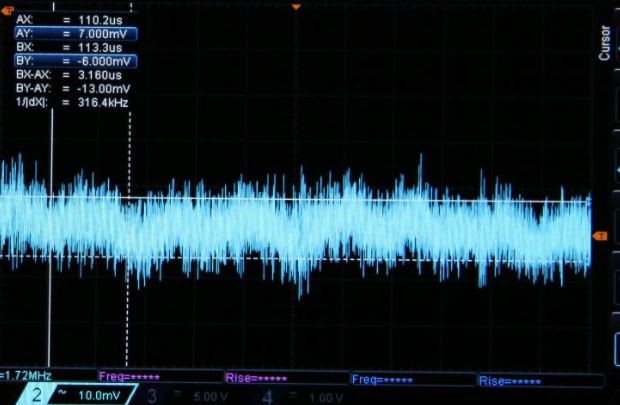
Now I have a comparison value: mathematically speaking, with 6.6 uF the ripple shall be 27 mAp-p. From the original 150 mAp-p this is 5.5 times lower. Here, 11 mVp-p of ripple corresponds to a reduction of 3.2 times from the original 35 mVp-p of the first reference acquisition.
I would say that considering the non-linearities of the flux/current characteristics of the LED, parasitics of capacitors, their tolerances, imperfections in the LED dynamic resistance and scope acquisitions far from perfect, this is quite a good result.
I would say that what was theorized in the previous log seems correct: a ripple of +/-2.5% can be achieved with a ceramic of 7.2 uF.
 Enrico
Enrico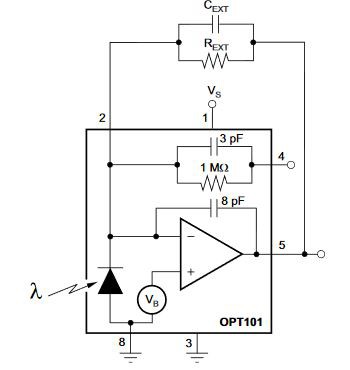
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.