It might be seem improbable to be able to calculate the probability of where the bearing balls will fall. Don’t Panic! every thing has an open source solution!

Yet under the assumes that the probability function of the ball distribution is a function of the Geometry of the pins and the radius of the bearing balls, it would be possible to calculate this probability for simple symmetrical shapes and certain ball radius to pin size proportion.
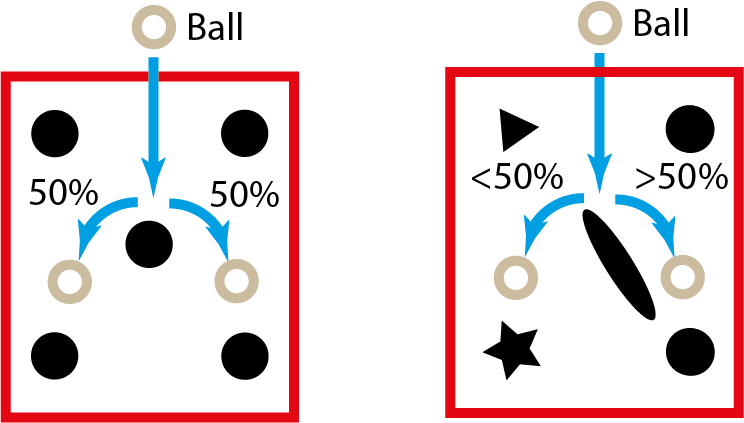
It’s by this logic that it is possible to calculate that for circle symmetrical pins in a quincunx formation, as probability for bounding to right of left of the pins becomes unbiased or equally probably. This will result in a binomial distribution of the bearing ball in the pins; explanation.
For random geometry this because much more default very quickly. Calculating the path of a ball for an biased fall probability is almost improbable. To still be able to estimate this probability numerical summation can be used to give a good approximation.
The simulation shows how bearing balls will fall in the bins, can be approximated using a simulation model of water falling from the top board over the bins of geometry. The simulation should be consider under the two considerations:
- As the water mas can be seen as an infinite number of infinite balls. The infinite number of balls insure that simulation will converge to the resulting probability
- As the bearing balls are of finite size, the quality of this approximation will depend of the proportion of the radius of the balls to the characteristic length of the spacing between geometry. The characteristic length being a function or to simplify an average of the value of the spaces between the pins.
For a larger spacing between the geometries, the balls will behave more like a fluid and the simulation results match the bearing ball distribution. With this in mind the simulation becomes a helpful to test the results.
Things will get more interesting for more complex geometry:
# Running The Simulation
The simulation uses the InterFoam Solver for two incompressible, isothermal immiscible fluids using volume of fluid phase-fraction based interface capturing approach, with optional mesh motion and mesh topology changes including adaptive re-meshing, see Wiki for more information about the solver. The Simulation uses RANS-Based turbulence modeling.
The simulation can be easily reproduced using the open source library OpenFOAM (Open Source Field Operation and Manipulation). It possible to run the simulation on linuxbe simply installing OpenFOAM or on windows or mac by installing Docker.

After OpenFOAM or Docker has been installed download the simulation configuration files for the repository. The simulation folder has also includes OpenSCAD file that should be used to generate the STL of the board of the board. The generated geometry should be named
```bash
board.stl
```
and placed within the folder
```bash
/contant/triSurface
```
For basic used the simulation is only configured to ran with this OpenSCAD file and using the same bounding geometry for the board. The simulation’s results will be valid only for variations of the pins on the board or any geometry based in place of the bins. For other board geometries the simulation code would still be valid by the configuration files should be adjusted.
To run the simulation can be stated by navigating using PowerShell(windows) or Terminal to the simulation folder and running the command:
for Linux, Windows or Mac first run:
```bash
docker run --rm -it -v ${PWD}:/home/openfoam openfoam/openfoam6-paraview54 /bin/bash
```
then run the command to start the simulation :
```bash
./Allrun
```
!!! Attention: The simulation will take about 6-12 hours depending on the used hardware and the will use about 5 GigaBytes of Hard disk memory!!!
To view the results open the file using paraview.:
```bash
results.OpenFOAM
```
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.