Bibhorr formula is a scientific equality that establishes relations between linear space dimensions and angular measures. When applied over triangle, the formula proves useful as a mode of aggrandizing the approximated trigonometric calculations.
Bibhorr formula is a concrete summary of the inaccurate trigonometry concept. This single equation defies the whole trigonometry concept.
The formula is written as follows:
where shrav श्र is the longest side, lambu लं is the medium side, chhutku छ is the shortest side and the Bibhorr angle is बि.
Conventional approach in trigonometry employs trigonometric functions like sine, cosine, tangent, etc. While the sophisticated “Bibhorr formula” replaces all the functions by geometrically linking the sides and angle of triangles. The superiority of the formula lies in the fact that it unveils an ideal side-angle model by incorporating the mathematical elements into a singular equation.
The applications of Bibhorr formula are quantum physics, space travel, teleportation, aerodynamics, propulsion, navigation and more.
The formula is devised using two inevitable constants named after Bibhorr. The constants that have been named ‘Bibhorr constant’ and ‘Bibhorr sthiron’ are 1.5 and 90º respectively. The elements of triangles are notated in Hindi or Devanagari letters making it the only standardized scientific representation.
The further modification of conventional equations with Bibhorr formula paves the way for a superior mathematics. Bibhorr formula acts as a barricade for the conventional trigonometry approach as it could detect previously unnoticed errors in trigonometric computations.


 Anteneh Gashaw
Anteneh Gashaw
 Discreet Mayor
Discreet Mayor
 Robert L. Read
Robert L. Read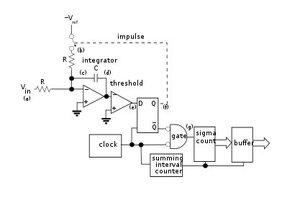
 glgorman
glgorman
I think it's interesting. To be honest, the trigonometry isn't my strong point. I've used the Essayontime platform to get some help with my college assignment in this filed. But the materials provided by https://essayontime.com.au/trigonometry-assignment-help really helps me to understand the core items of it. I think that your project can be useful for students.