Divide and Conquer (Option 1)
After playing with the Options presented in my first post, I have decided Option 1 is the best. Why? It should have the least number of the expensive reverse kinematic calculations. Consider a very coarse tolerance (=128):
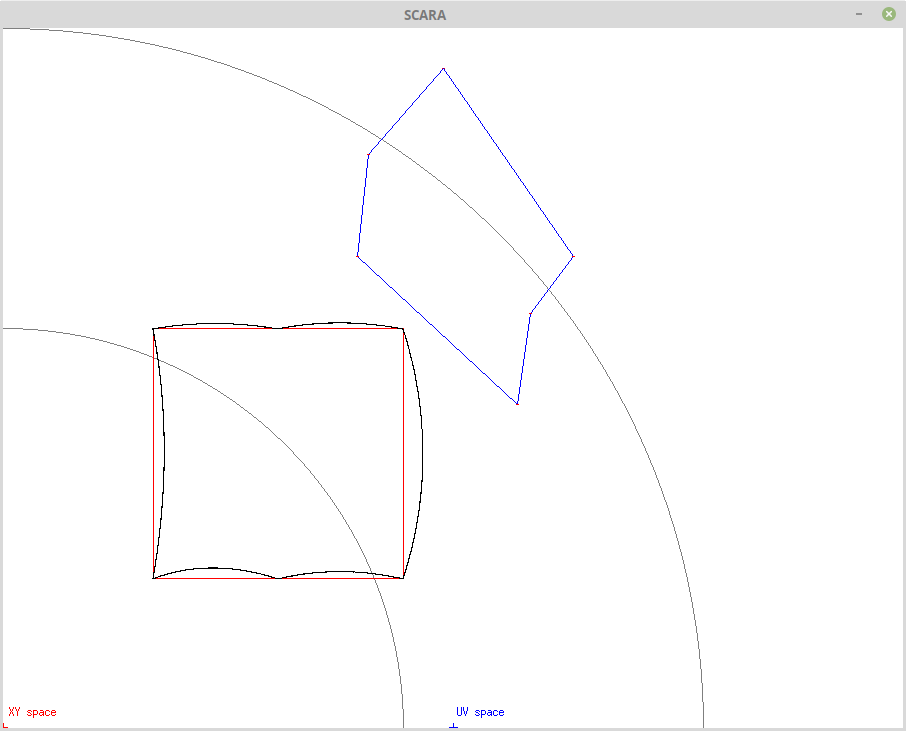
Note that the UV space (blue lines) has only 6 points (the straight lines between them are Bressenham lines).
Now the medium tolerance case (=32):
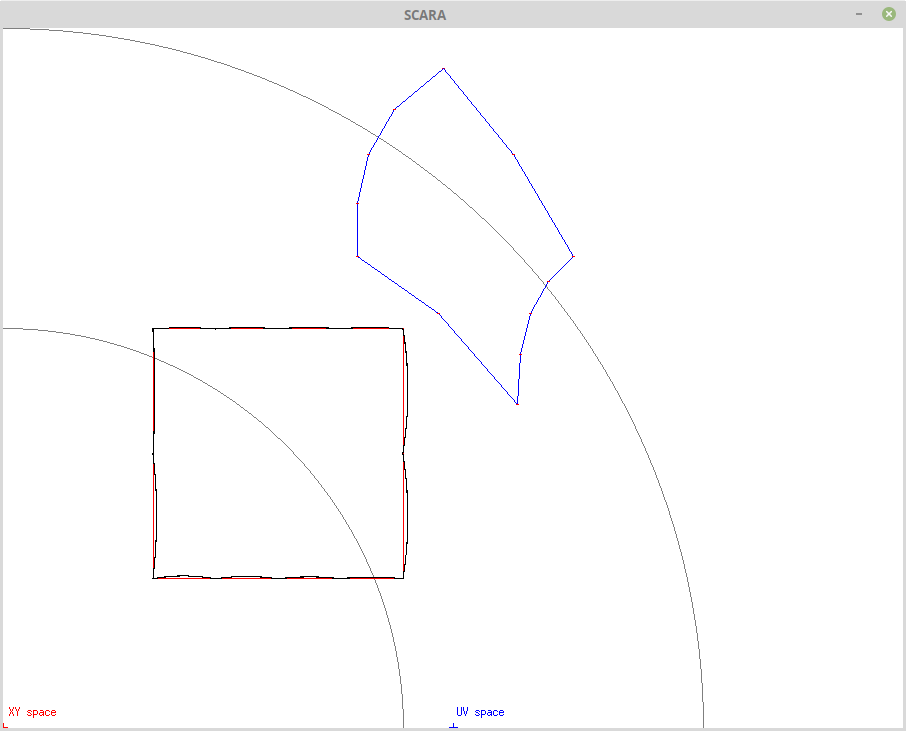
Here there is only 13 reverse kinematic calculations.
Now the very fine tolerance (=8):
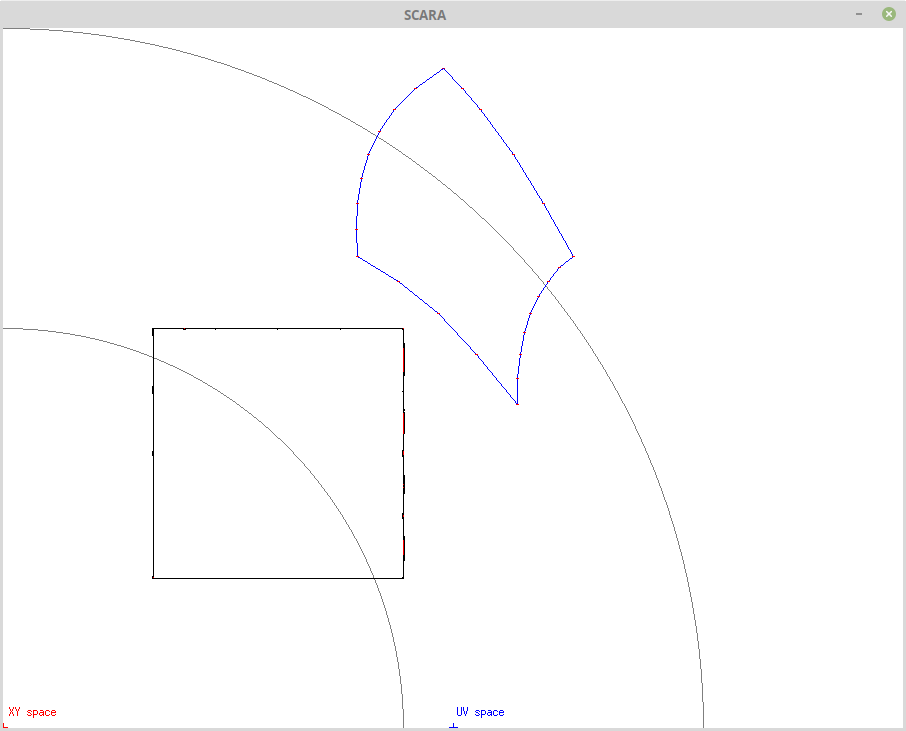
Here there is only 25 reverse kinematic calculations.
Finally ultra fine tolerance (=1), has 67 calculations:
![]() Fast Trigonometry
Fast Trigonometry
Although the number of reverse kinematic calculations are a minimum, there still may be advantage is fast (integer?) methods. The CORDIC algorithm comes to mind, especially for the ATAN2() and sqrt() functions. ArcSin/ArcCos should also be possible.
Here is my version of Rect2Polar (i.e ATAN2() and sqrt()) using short (i.e int16) integers:
// Include libraries
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <string.h>
#include <math.h>
#include <stdbool.h>
void rect2polar(short X,short Y,short *R,short *A)
{
// ATAN_Table is the values of ATAN(1/(2^i))*400*32/2/Pi micro-steps
short ATAN[12]={1600,945,499,253,127,64,32,16,8,4,2,1};
short i,Xnew,Ynew;
(*A)=0;
if (X<0) {
(*A)=200*32; // 180 degrees
X=-X;
Y=-Y;
} else if (Y<0) {
(*A)=400*32; // =360 degrees
}
for (i=0;i<12;i++) {
if (Y<0) {
// Rotate CCW
Xnew=X-(Y>>i);
Ynew=Y+(X>>i);
(*A)=(*A)-ATAN[i];
} else {
// Rotate CW
Xnew=X+(Y>>i);
Ynew=Y-(X>>i);
(*A)=(*A)+ATAN[i];
}
X=Xnew;
Y=Ynew;
}
// Adjust for gain (=X*0.607252935)
X=X>>1;
(*R)=(((((((((((((((((X>>2)+X)>>2)+X)>>1)+X)>>1)+X)>>2)+X)>>1)+X)>>2)+X)>>1)+X)>>3)+X;
}
int main(void) {
short A,R,X,Y;
X=-439*32;
Y=-439*32;
// R=621*32 max
rect2polar(X,Y,&R,&A);
printf("Rect2Polar x %8.3f y %8.3f ang %8.3f hyp %8.3f\n",X/32.0,Y/32.0,A*360.0/400.0/32.0,R/32.0);
printf("atan2() x %8.3f y %8.3f ang %8.3f hyp %8.3f\n",X/32.0,Y/32.0,360+atan2(Y,X)*180/M_PI,sqrt(X*X+Y*Y)/32.0);
return 0;
}
Here is the result:
$ ./ShortCAtan
Rect2Polar x -439.000 y -439.000 ang 225.028 hyp 620.812
atan2() x -439.000 y -439.000 ang 225.000 hyp 620.840
$
So about 4 digits of accuracy with 16 bit integers.
Reverse Kinematica
I reworked the mathematics to suit CORDIC:
- R=sqrt(X*X+Y*Y);
- A0=atan2(X,Y);
- A1=A0-PI/2+asin((L1*L1+R*R-L2*L2)/L1/R/2);
- A2=PI/2-asin((R*R-L1*L1-L2*L2)/L1/L2/2);
- X=cos(A1)*L1+cos(A1+A2)*L2;
- Y=sin(A1)*L1+sin(A1+A2)*L2;
ArcSin CORDIC
Here is my ArcSin CORDIC:
// This version works properly but has a multiplication in the main loop
short arcSin(short R, short S) {
// ATAN_Table is the values of ATAN(1/(2^i))*400*32/2/Pi micro-steps
short ATAN[12]={1600,945,499,253,127,64,32,16,8,4,2,1};
// SEC[i]=(int)((1/COS(ATAN(1/(2^i)))-1)*(2>>14)+0.5);
short SEC[15]={6787,1935,505,128,32,8,2,1,1,1,1,1,1,1,1};
short i,Rnew,Y,Ynew,A;
Y=0;
A=0;
for (i=0;i<=11;i++) {
if ((Y<S)&&(A<100*32)) { // 90 degrees
// Rotate CCW
Ynew=Y+(R>>i);
Rnew=R-(Y>>i);
A=A+ATAN[i];
} else {
// Rotate CW
Ynew=Y-(R>>i);
Rnew=R+(Y>>i);
A=A-ATAN[i];
}
Y=Ynew;
R=Rnew;
S=S+((S*SEC[i])>>14);
}
return A;
}
The down side of my ArcSin CORDIC is the multiplication inside the main loop. I remember I had to do the multiplication to avoid instability.
AlanX
 agp.cooper
agp.cooper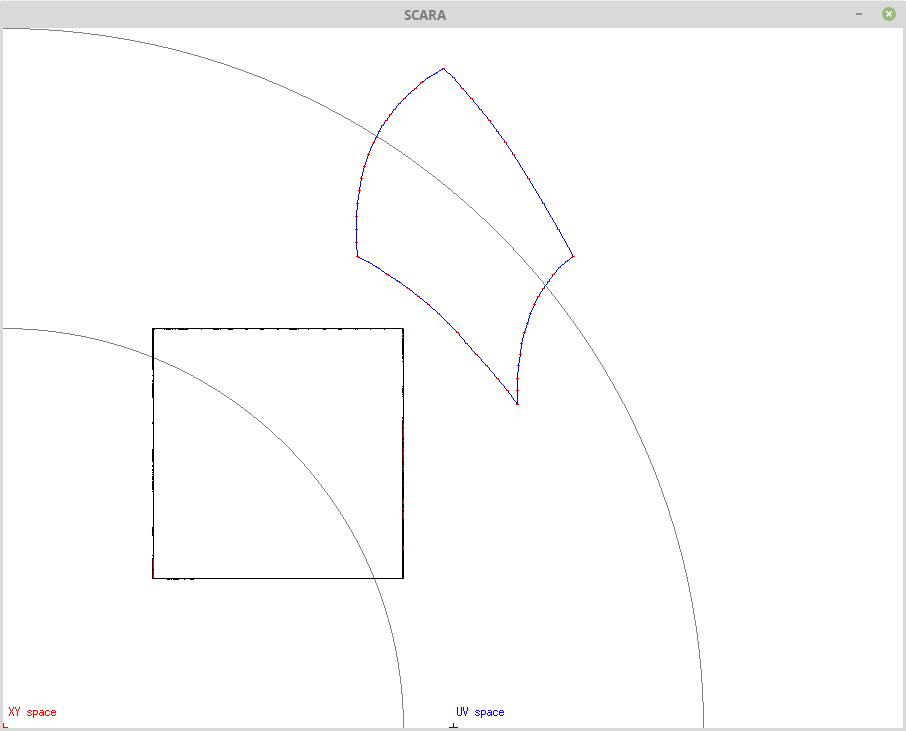 Fast Trigonometry
Fast Trigonometry
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.