The CPU state machine was introduced early in the project and has undergone some evolution as the design progressed. Hopefully things are stable enough to expand on the details.
The CPU essentially does the same thing on every instruction cycle: It fetches an instruction and then latches data from the ROM in to a register. The instruction always comes from the program bank of the ROM, the data can come from either the program half or ALU banks. In the case of the program bank, the data would be an operand. The ALU banks return the result of an arithmetic or logical operation.
Every instruction cycle begins with an instruction fetch, which can be either one or two bytes in length. The upper bit (i7) of the first instruction byte determines if another instruction byte should be fetched. Once the instruction is fetched an operand or ALU result will follow. In the case of the ALU, either the H or L register can be selected as the input to the ALU, or in the case of 8-bit operations, both the H and L are used sequentially. A conditional option also exists where the operand fetch can be skipped based on the sign of the accumulator. If the condition is not met then the CPU will skip the second part of the cycle and fetch the next instruction immediately.
If any of that made sense then you'll be aware of 4 possible sequences:
- Single Cycle - conditional operand fetch where condition is not met (NOP)
- 2-Cycle - Single byte instruction, fetch operand, or 4-bit ALU operation.
- 3-Cycle - Two byte instruction, 4-bit ALU operation.
- 4-Cycle - Two byte instruction, 8-bit ALU operation.
This state can be handled with a 2-bit finite state machine. The op code is encoded using the top 3-bits of the first instruction byte (i7-5). Only the H register is used for the 2-cycle ALU operations and is also used when i6 is high in the 3-cycle operations. If i6 is low then the L register is used, and if i5 is low then the state machine will progress to a 4th cycle and use the H register as well. The NOP will keep the state machine in the initial instruction fetch state, which is also the reset vector.
Even though this may sound complex, the state-transition diagram should be easy to follow:
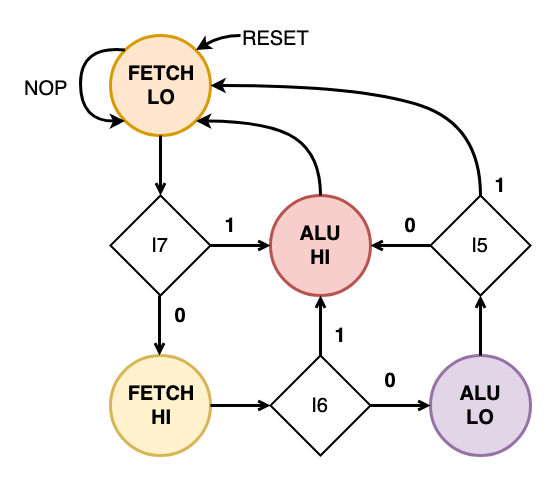
It takes two D flip flops and about a dozen gates to implement this state machine. There are two other simple state machines used as well: One is used to cache the sign of the accumulator (1-bit) and the other selects the boot page (1-bit). The boot page is needed to clear the page register after a reset. The page register is left in tri-state and pulled high to 0xFF on reset and left that way until a negative conditional register load is completed. This way a boot sequence can be executed on start up and cleared when an initialization loop ends. These require another two D flip flops and dozen gates.
All this can be implemented with TTL chips and the initial design was able to fit this in about 6 chips. Another option was to use Programable Array Logic. The requirements are simple enough to fit one of the original (circa 1978) PAL chips, the PAL16R4. This provides 8 inputs, 4 combinational logic outputs, and 4 registered outputs for the state machines.
The additional combinational outputs are used to provide control signals derived from the state machines:
- PA17 - (pin 19) A17 for the ROM
- PA16 - (pin 18) A16 for the ROM
- !prog - (pin 13) select program/page registers (active low)
- pcent - (pin 12) Program Counter clock enable (active high)
The registered outputs are assigned as follows:
- sign - (pin 17) sign of the accumulator after the last ALU operation
- boot - (pin 16) boot mode (active high)
- hsel - (pin 15) HL register select (1 = H, 0 = L)
- !fetch - (pin 14) instruction fetch (active low)
The layout and pinout of the PAL can be seen below, where the inputs assigned as follows:
- !reset - (pin 2) Reset (active low)
- pclk - (pint 3) processor clock
- hblank - (pin 4) horizontal blank (active high)
- DD7 - (pin 5) sign bit of accumulator (1 = negative, 0 = zero, or positive)
- I4..7 - (pin 6..9) high nibble of lower instruction register
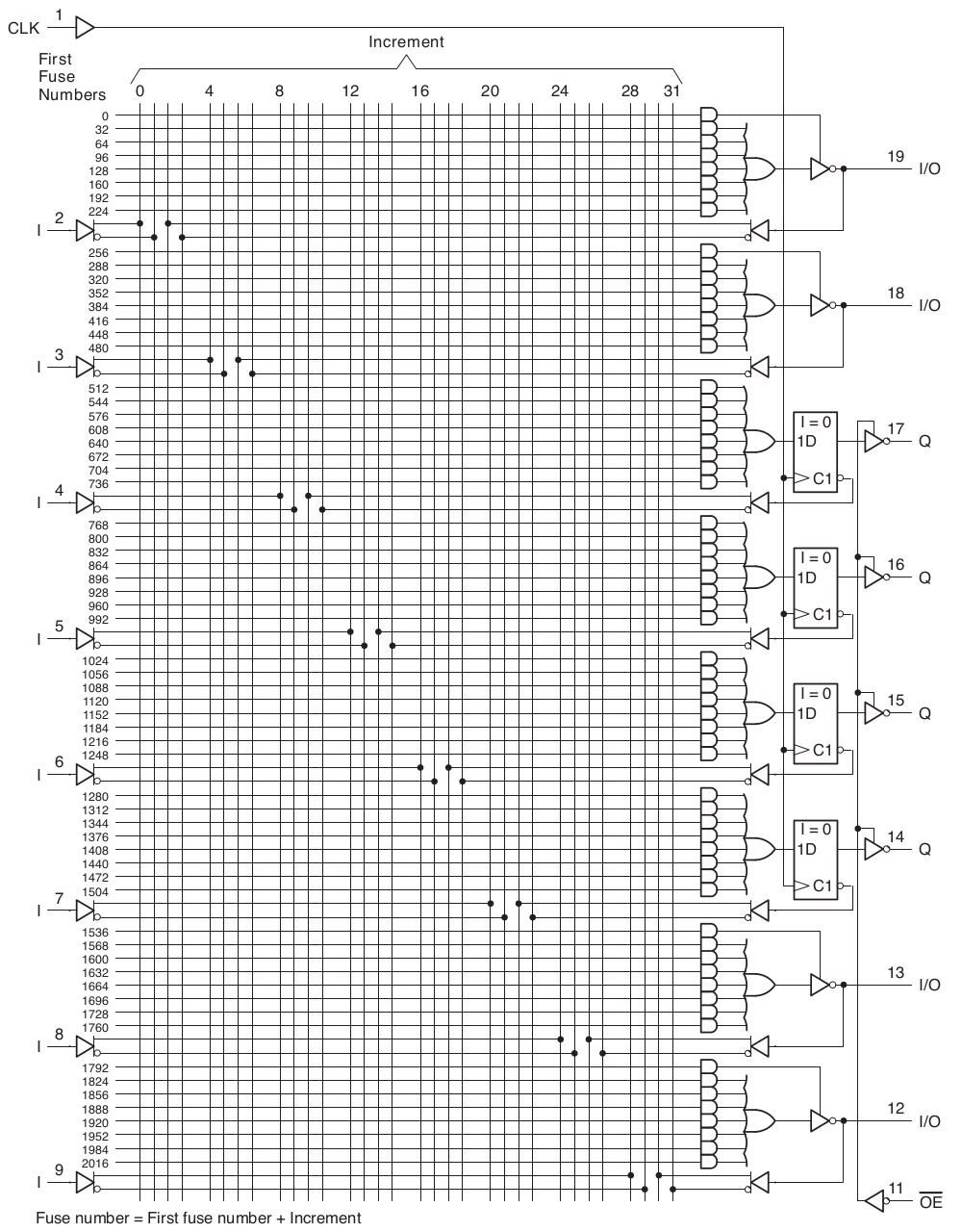
The exact logic functions can be seen in the GitHub repo. The compiled version is shown below as a 2048-bit mask where each zero represents a connection in the grid above.
11110111111111111111111011111111
11110111111111111111011101111011
11110111111111111111111110110111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11110111111111111110111111111111
11110111111111111111111111110111
11110111111111111111111101111111
11110111111111111111011111111111
11111011011111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111001111111110111111011
11111111110111111111111011111111
11111111110101111111111111111111
11111111110111111111111110110111
11111111111001111111110101111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
10111111111111111111111111111111
01111111111111011111111101111111
01111111111111011011111111111111
01111111111111011111111011111111
01111111111111011111101111111111
01111111111111011111111111111011
11111111111111111111111111111111
11111111111111111111111111111111
01111111111111111110111010111111
11111111111111111101111011111011
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111110100110111011
01111111111011111001011011110111
01111111110111110101111011110111
01111111111111110101101011110111
01111111111111111101111001110111
11111111111111111110111001111111
01111111111111111110111010111111
11111111111111111111111111111111
11111111111111111111111011111111
11111111111111111111111110110111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11110111111111111111111110110111
11110111111111111111111011111111
11111111110111111011011110110111
11111111111011110111011110110111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
The original PAL16R4 is no longer available, but there is a modern equivalent in the ATF16V8B. This is a GAL (generic array logic) which can be programmed to resemble a variety of PAL devices including the PAL16R4. The GAL contains 250 gates, but only 80 of these are used as follows:
- 32 AND gates
- 8 OR gates
- 4 registers (10 gates each)
 Alastair Hewitt
Alastair Hewitt
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.