Primitive data types are an interesting subject to tackle. They are technically defined by programming languages, not hardware, so I am a little out of my field. Nevertheless, it's vital to explore the possibilities and variations that come about with a balanced ternary system. Everything I put forward here is really just intended to get some of my ideas documented. The implementation details would be up to the designers of the programming languages, a task I am not really qualified to undertake.

When I say primitive data type, I'm talking about the "C style" types that map directly to objects in memory of a pre-defined size (some portion or multiple of the processors word length). They can be manipulated directly by individual processor instructions, like in assembly. I am also limiting this post to value types and not reference types such as pointers, references, classes and such.

The hypothetical systems I am thinking about would have word lengths of 27 trits or 54 trits. These would far exceed the capacity of a 32-bit system or a 64-bit system respectively. In a previous post I said a 45-trit system would be sensible because it would exceed a 64-bit system and is divisible by both 3 and 9, but then I realized it is not an even multiple of 27. Moving up to 27*2=54 trits would probably be the next logical step up from a 27-trit word length.

Let's start with the usual lineup of commonly recognized primitive data types. The values given are common mappings, but not necessarily true in all implementations. I'm using C style primitives because that is the lowest level programming language that most people are acquainted with.

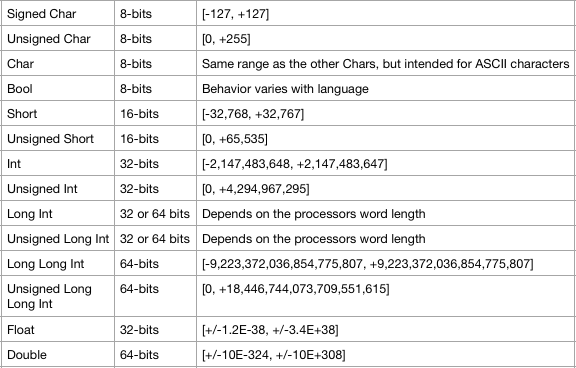
Breaking this down, we have several integer types, either signed or unsigned of various sizes. Then there is a pair of special integer types for portability across systems that could have dissimilar word lengths. Next we have a special 8-bit type for ASCII characters. Then there are some floating point types and the boolean type.

Now on to the primitive data types of our imaginary world where 27-trit and 54-trit balanced ternary computers, microcontrollers and digital signal processors are commonplace. First off, all this signed and unsigned stuff can go out the window! Balanced ternary numbers are natively signed or unsigned by their value alone. Therefore, we would only need the following integer types:

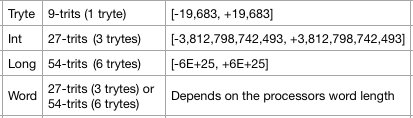
That handles signed and unsigned numbers well beyond 32-bit or 64-bit equivalents. The "word" type also allows programs written for the smaller architecture to run on the larger without worrying about weird integer problems. Just like with existing systems, programs written for the larger architecture could still get bugs due to truncation if compiled on the smaller architecture. The Tryte is useful to have because there does need to be an efficient scheme for packing arbitrary data.

We would also need floating point number types:

The 27-trit float is not just in my imagination. A formal proposal has already been written and submitted for peer review. The 54-trit float is total fantasy at this point but that word length should be capable of exceeding the range and precision of the x86 80-bit double double. It would definitely not exceed the range/precision of a 96-bit or 128-bit long double.

Next, we should have data types for human readable characters. I suggest a char type that is the full 27-trits but is explicitly not an integer. It would be large enough to hold a full-sized UTF-32 Unicode character. This could seem rather wasteful of space, but that isn't the same major concern it once was. Further, the 9-trit tryte exists and could be used to allow a string of tiny UTF-8 or ASCII characters taking up whole 27-trit chars to be efficiently packed if they needed to be transmitted or if space constraints were severe. That is more of a language specific implementation detail.

But how do we handle boolean values on a balanced ternary computer and how to handle the relative "truthiness" of 0 in a balanced ternary system? I propose two "factuality" data types:

Note that I am adopting NEUT or NEUTRAL as a label for the 0 value. I have been using "intermediate" in earlier posts, but it just takes too long to write and the abbreviation makes it look like you are talking about integers.

In some languages, like C (prior to C99) you don't have an actual boolean data type at all, but the comparison operators will treat integers with any non-zero value as TRUE and integers with a value of 0 as FALSE. With C99 you can include stdbool.h and get an actual boolean data type where any non-zero value that is assigned to it is changed to a 1 so that the variable can only contain a 0 or a 1. Python does essentially the same thing. I strongly favor the C99/Python way of handling bools and encourage the same behavior with Kleenes except that the FALSE value would be represented by a string of zeros followed by a - in the least significant trit, a NEUTRAL would be represented by all zeros and TRUE would be represented by a string of zeros followed by a + in the least significant trit.

One should be able to cast a bool into a Kleene with a 0 value converting into a - so that FALSE conditions are maintained as FALSE. A Kleene would have to have NEUT clamp down to FALSE or up to a TRUE if one were cast to a Bool. Or the compiler could just throw an error (seems like a better idea to me).

Using a three-valued bool-like data type is actually not very original. They've been around since the 70's and are currently used in many programming languages including Perl, PHP, Ruby, Haskell and others. It is currently in the C++20 proposal as well so we may be seeing it in C++ soon. These are returned by a special comparison operator, usually denoted by <=> or <==> (spaceship operator), which compares two values and returns an integer value -1 if x < y, integer value 0 if x == y or integer value 1 if x > y. In C, the functions strcmp, memcmp and qsort return the same thing. The output of these functions is essentially a kleene data type. A kleene however, would be general purpose, not just constrained to a few specialized comparison operators.