Huffman Encoding (and decoding) is very commonly used compression algorithm. It is often used in conjunction with other compression techniques but can also be used by itself. The idea is to count up each time a digit pattern (such as a bytes, 16-bit words, 32-bit words, etc.) appears in a file and then rank each pattern by how common it is. For example, if you had a file where the byte 01001100 appeared more frequently than 01001111, then the first would have a higher “score”.

After ranking the digit patterns, you assign the most commonly used bytes (or words, Unicode values, etc.) a short code-word and you assign the least commonly used bytes longer code-words. Because the bytes are being assigned code-words of differing length, this is called a variable-length encoding algorithm. The result of applying the Huffman algorithm to a file can be stored as a binary tree to aid in decoding.

The decoder on the receiving end will not know where a code-word begins or ends. To handle this, the assignment of code-words must adhere to a rule known as the prefix property. This means that no code-word may appear as the prefix to another code-word. For example: If a byte is assigned the code-word “0”, then no other code-word can begin with “0” since the first one would be the prefix of it. If a byte were assigned the code-word “110”, then “11001” would be an invalid code-word because it is prefixed by “110”, but “101100” would be valid since “110” is contained inside, not at the beginning. Sharing prefixes is okay, such as “1110” and “1111”. Both start with “111”, but as long as “111” isn’t itself a code-word the prefix property is not violated.

To adapt this to a balanced ternary system, we would use a ternary tree rather than a binary tree. There is also one additional step that is not necessary in a binary tree. Just before starting the tree you must check to see if the number of items is odd or even. More on this later.

Let’s assume you are encoding a plain text file with the words “attack at dawn.” and want to compress it based on letter frequency. First, count up the letters, spaces, and punctuation:

a = 4

t = 3

c = 1

k = 1

space = 2

d = 1

w = 1

n = 1

period = 1

Then arrange them from least to greatest:

period = 1

n = 1

w = 1

d = 1

k = 1

c = 1

space = 2

t = 3

a = 4

Now is where you would check to see if the number of items is even or odd. There are nine items making it odd. In this case, the next step is to remove three items from the list and begin the tree from the bottom up. However, if the number of items on the list was even, you would only remove two items from the list. This is only done the first time when you are beginning the tree. Every other time you remove items from the list and add them to the tree, you do so in sets of three.

The number of items is odd, so remove the three lowest valued items from the list. There are several options that are equally low, so lets arbitrarily pick period, n, and w. These become leaf nodes with a new node above them. Each node is denoted with what symbol it represents and its frequency in the text being compressed. We then add the new node n0 to the list.

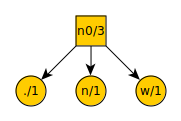
Our list now looks like this:

d = 1

k = 1

c = 1

space = 2

n0 = 3

t = 3

a = 4

We repeat the procedure of removing the three lowest value items from the list, placing a new node over them, and putting the new node on the list. Our ternary tree now looks like this:

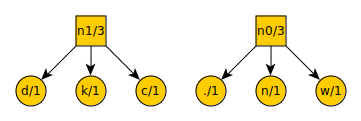
And our new list looks like this:

space = 2

n0 = 3

n1 = 3

t = 3

a = 4

After another iteration…

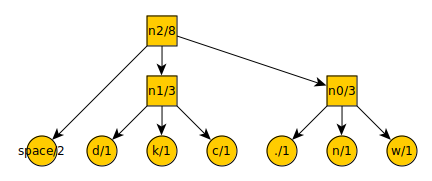
The list now contains:

t = 3

a = 4

n2 = 8

And finally:

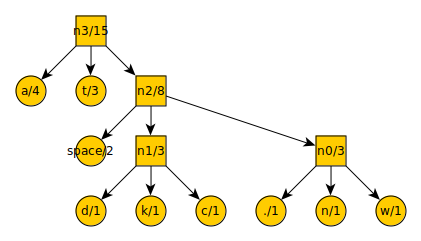
By starting at the top, you can count every leftward motion as a -, each downward motion as a 0, and each rightward motion as a +. This gives you the code-word for each symbol. The symbol “a” is encoded into the code-word “-”. The symbol “n” is encoded into the code-word “++0”.

Let’s say that the message had been “Attack at dawn”. The period at the end is omitted, so now there are an even number of items on the list:

n = 1

w = 1

d = 1

k = 1

c = 1

space = 2

t = 3

a = 4

We would only remove two items from the list, place a new node over them, and add that node to the list. Here is the tree:

And here is the new list:

d = 1

k = 1

c = 1

n0 = 2

space = 2

t = 3

a = 4

Notice that n0 has a value of only 2 in this instance. In the previous example it had a value of 3.

We now remove the three lowest value items from the list (the removal of two items is only done the first time). Here is the tree:

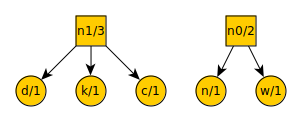
And here is the new list:

n0 = 2

space = 2

n1 = 3

t = 3

a = 4

The tree after another iteration:

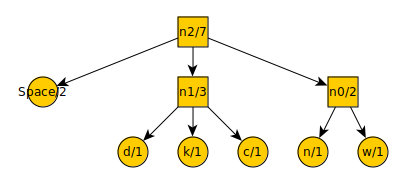
And the new list:

t = 3

a = 4

n2 = 7

Remove the final items from the list and add them to the tree:

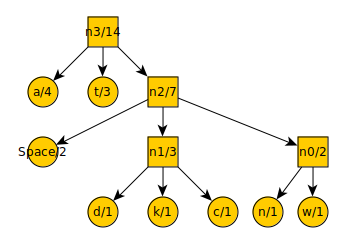
If we assume that each letter took 6 trits (which is just a bit more data than 8 binary digits), the total message would have been 84 trits long. The new compressed message reads as: -00-+++++0+--0+-++--++0++-. This is only 26 trits, a savings of 31%. If the difference between letter frequencies had been more pronounced, the savings would be greater.

To decode, the sender only needs to provide the encoded message and the ternary tree data structure. With these, the decoding program can correctly recover the original message by taking the trit-stream and following it down the tree. Every time it hits a leaf node, it returns the value stored in that node and starts over at the root node with the rest of the trit-stream.

Because the ternary tree has to be provided along with the compressed message, you lose a little bit of your savings to the space taken up by the tree data structure. However, this does not necessarily need to be the case. If the sender and receiver have previously agreed on a ternary tree in advance, based on prior knowledge about which symbols are likely to be common then the tree doesn’t need to be sent. Unfortunately, it also means that the tree won’t be perfect for any given message and therefore optimal compression won’t be achieved.

In the final analysis, there is little difference between binary and balanced ternary in how the algorithm behaves. Nevertheless, it was good to sort out little details like the necessary check for evenness or oddness.