Scope
The scope of this project is to document the coding of a rather complex problem.
Basic Code
To begin I need:
- a "segment" intersection routine
- an offset routine
- some test data
I have decided to truncate intersection "rays" in the basic code.
Note: a segment is line bounded by two points while a ray is an infinitely long line.
Resolving Cross-Overs
Resolving cross-overs can wait until the basic code works as well as it can.
Initial Experiments
Initially to test the two main routines I built a program that steps through increasing angles for two joined segments:
Here is the first case where the offset segments intersect:
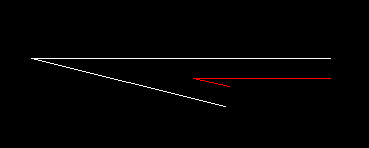 Note: the white polyline is the original polyline and the red polyline is the offset polyline.
Note: the white polyline is the original polyline and the red polyline is the offset polyline.Here is the second case where the offset polylines intersect because I have extended the offset segments the offset distance:
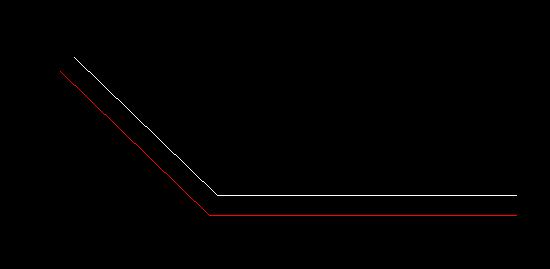
Here is the third case where the intersection exceeds the extended offset segment. In this case I have truncated the offset polyline:
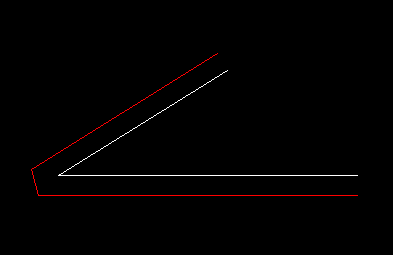
This truncated offset polyline is fine for CNC mill or laser cutting applications.
The last case is problematic:
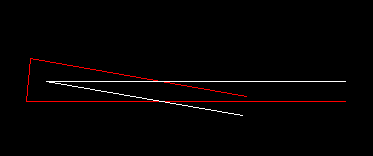
I have to either accept this or a ray intersection.
After a lot experimentation, I decided to accept the ray intersection.
A final case to consider is co-linear segments. The two spikes are co-linear segments:
Next Set of Experiments
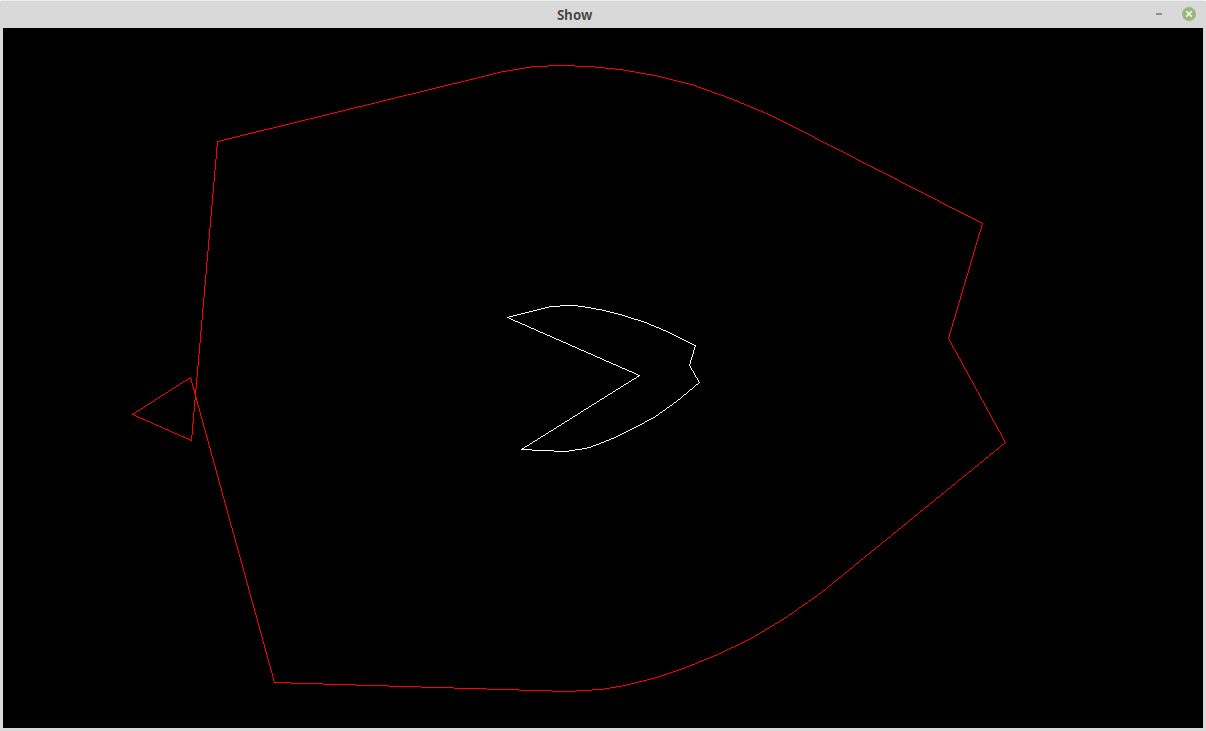
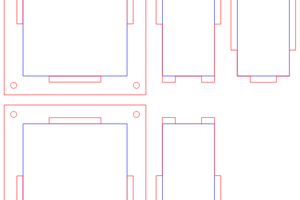
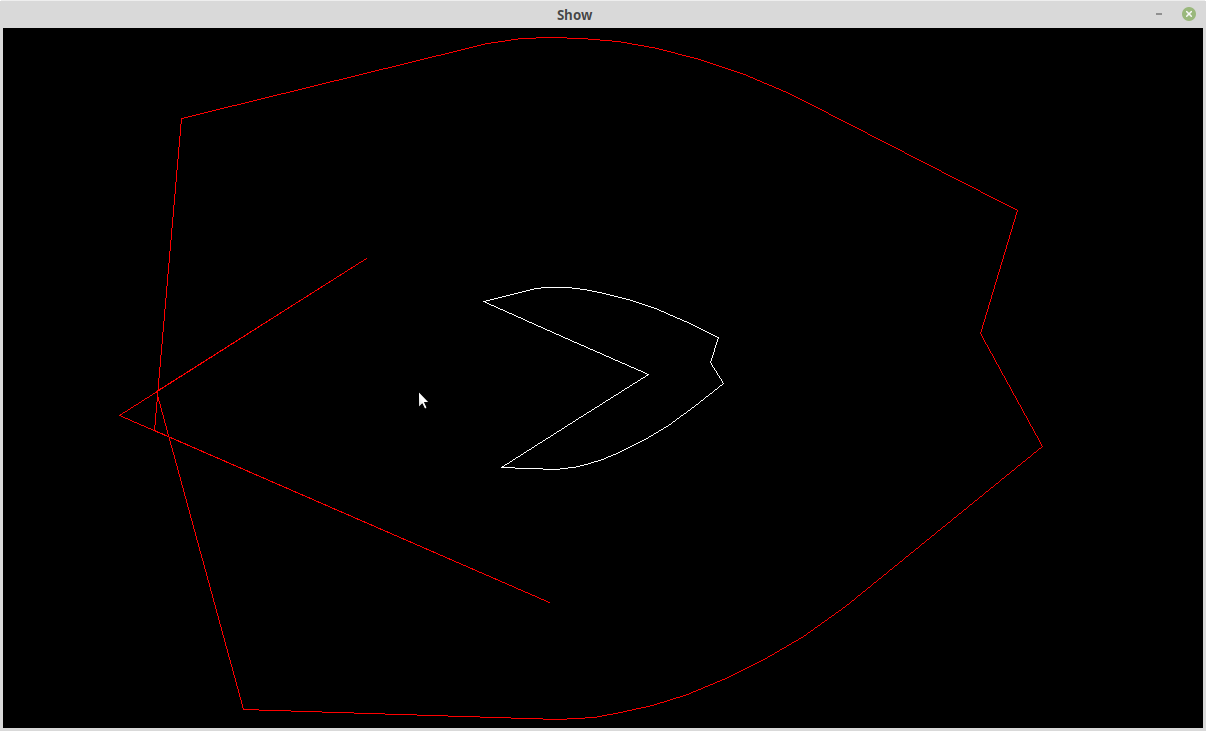
Here is my test data (the white closed polyline) for the next set of experiments:
For this experiment I filtered the original (i.e. the white polyine) for near co-linear segments and very short segments. Although the original polyline appears symmetrical, the location of the points are not.
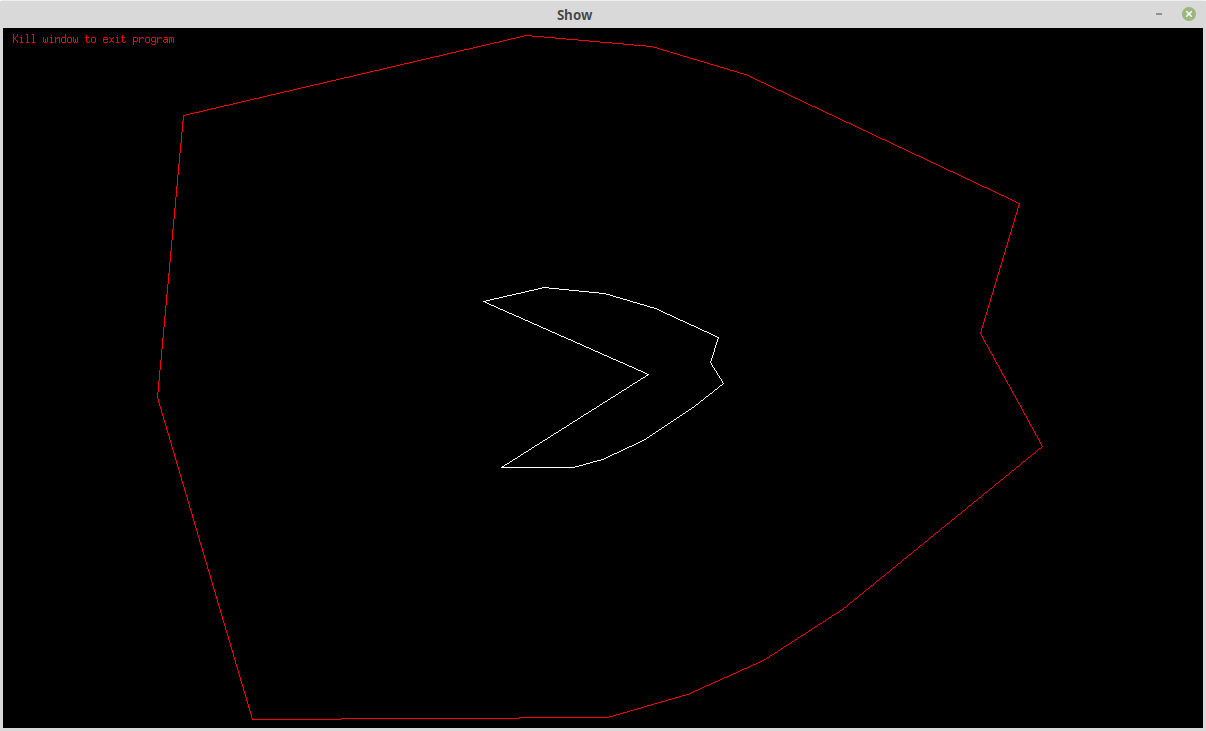
Hers is the contraction case:
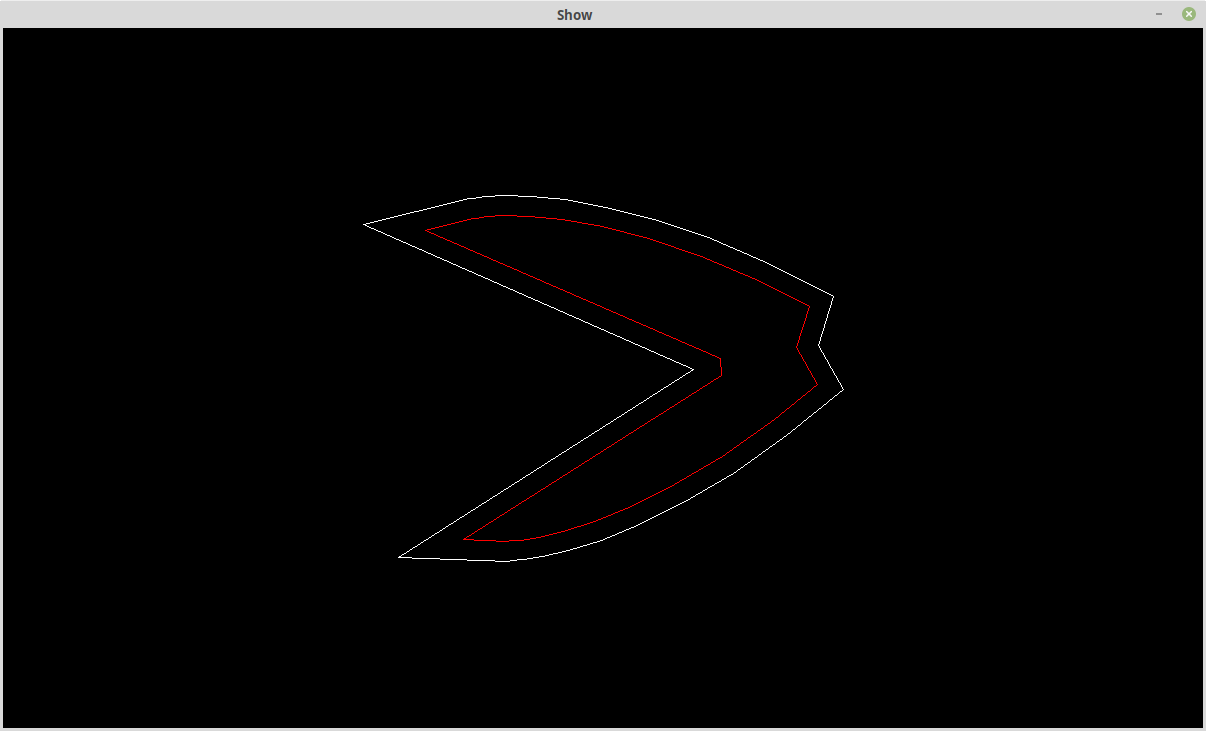
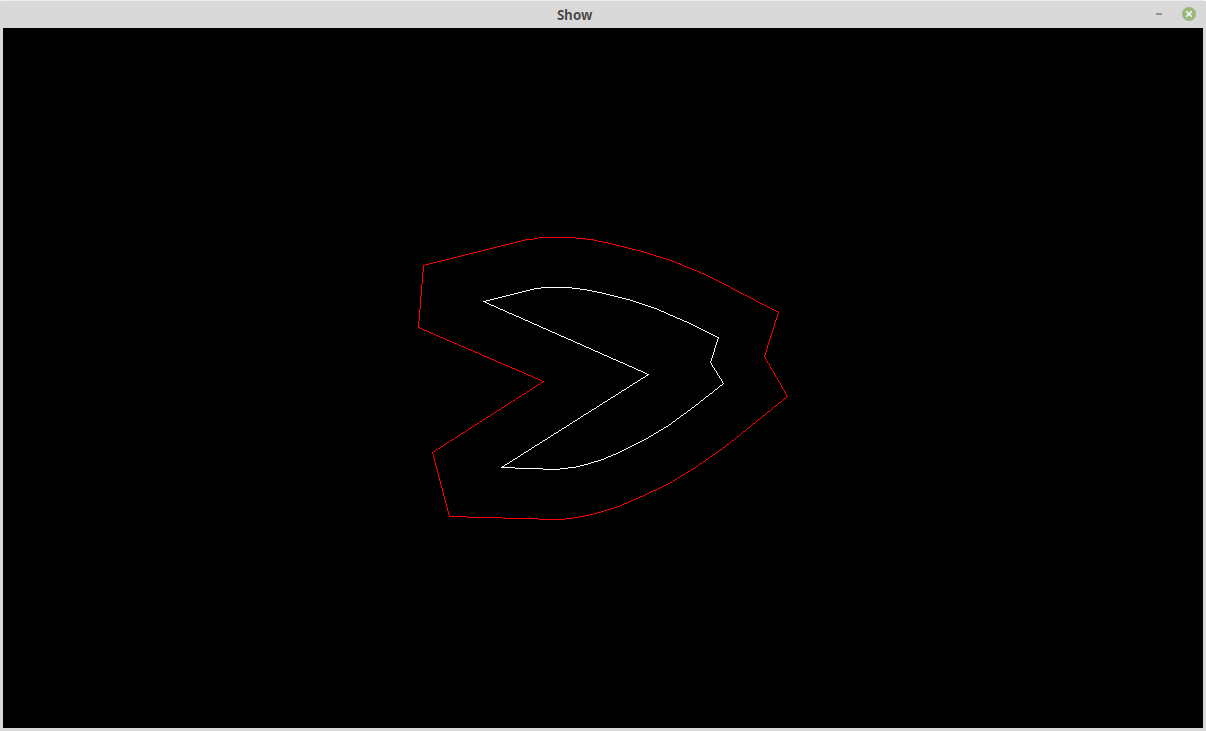
If I expand or contract the original polyline sufficiently problems appear:
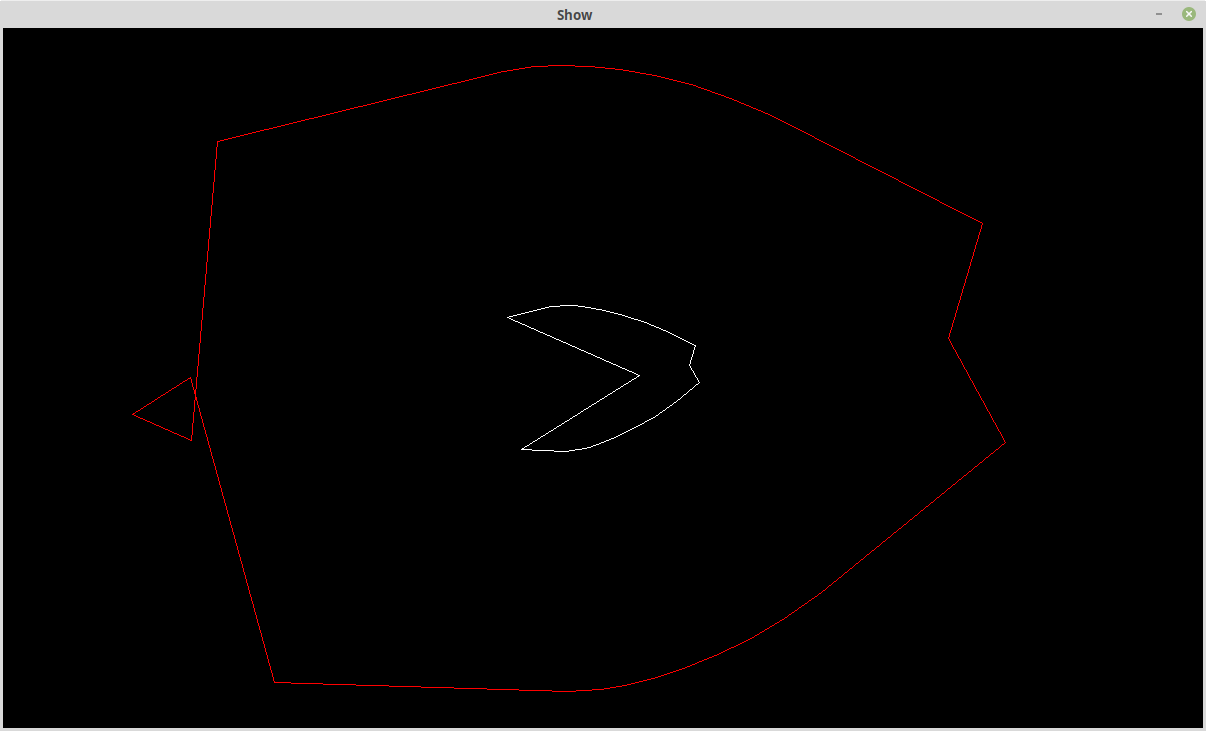
Note the offset polyline cross-over.
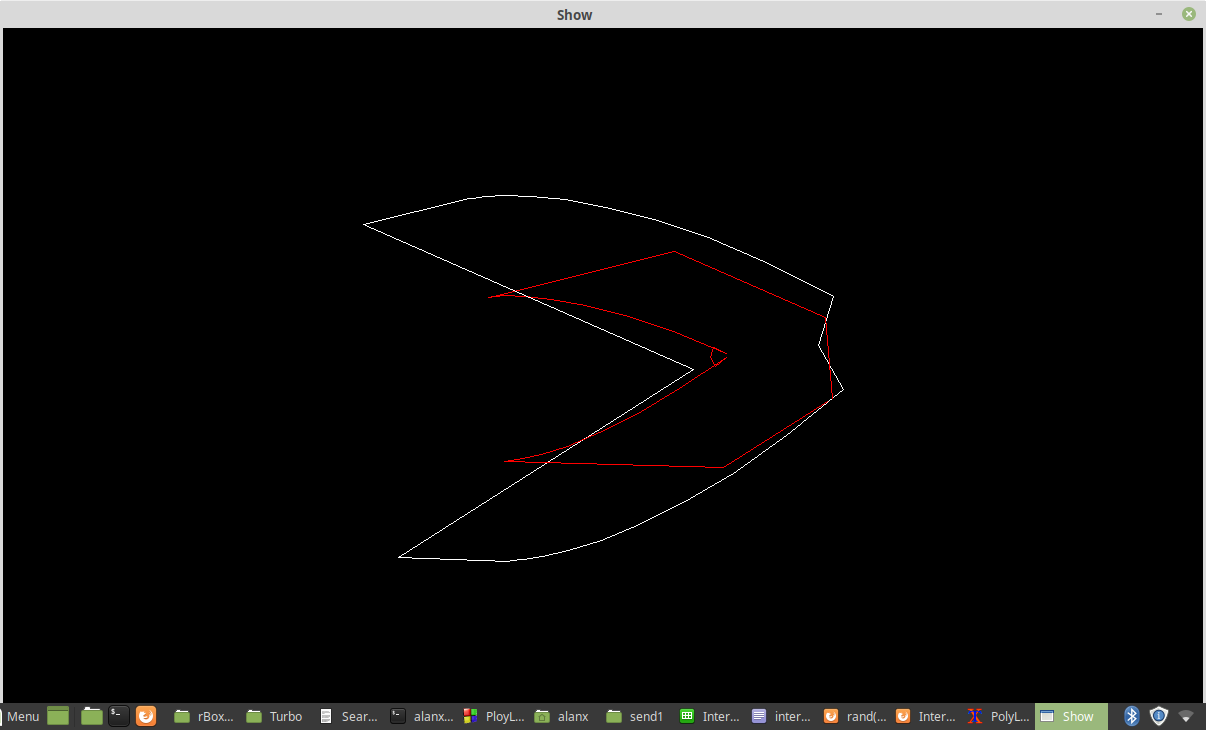
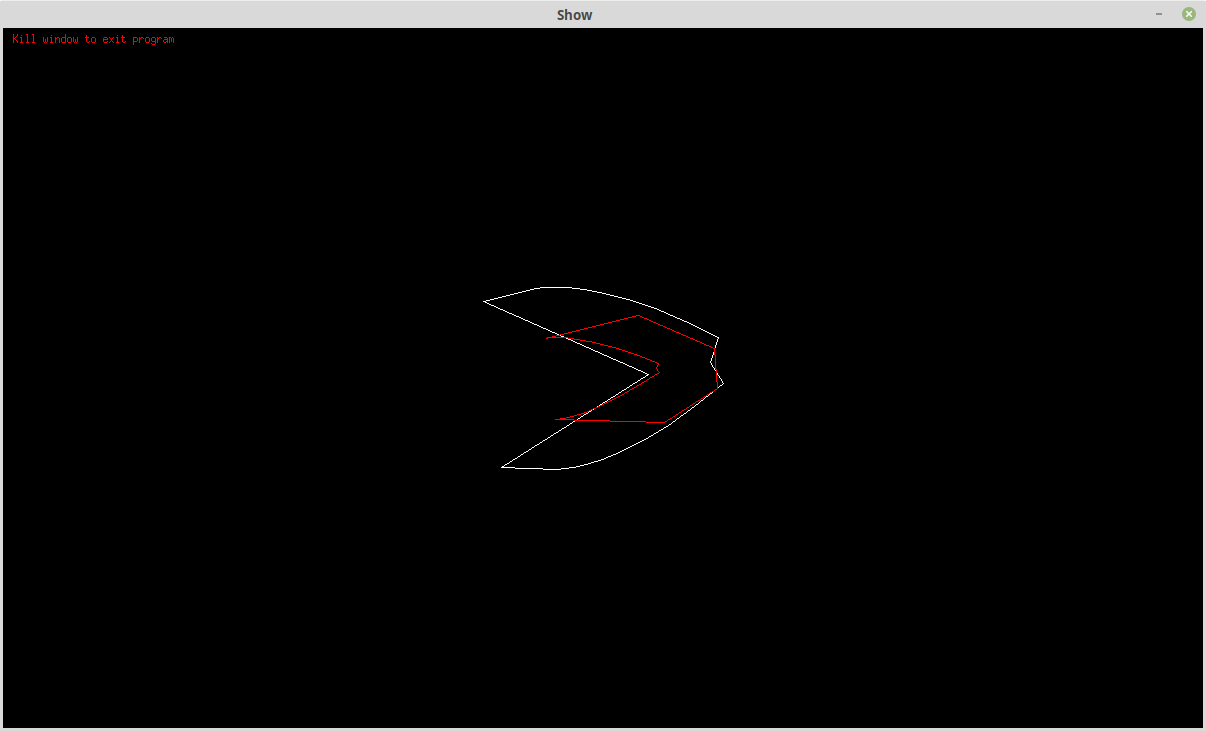
And:
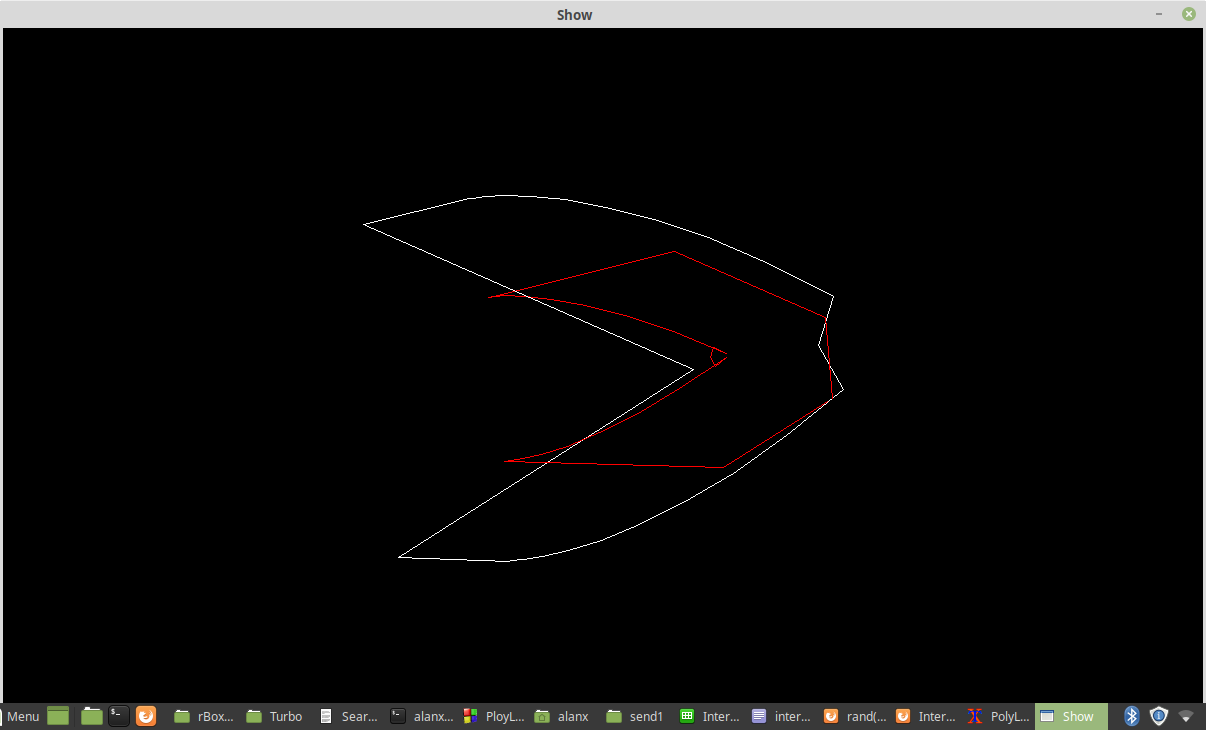
In this case the offset polyline has reversed direction. The offset polyline is also distorted due to the order of the offset point intersection truncation.
Status
At this point of time I have basic working code. There is potential to improve the code by resolving cross-overs and taking another approach to ray truncation.
AlanX
 agp.cooper
agp.cooper