Some interesting progress with automatic tuning. To review, I have modeled the 40 meter loop antenna with a coil made from thin copper tubing. Initial testing is with a 100 pf capacitor. Later testing will be with a motor-driven variable capacitor. A sweeping RF signal is coupled to the tuned circuit with a nearby multi-turn link that is roughly 50 ohms at 7 MHz. (This simulates the exciter loop of the loop antenna.) For detecting resonance, the signal is sampled with a FT-43 toroid transformer. The primary is made by passing a wire through the toroid. The secondary is a tuned link with magnet wire.
The current goal is to find the resonance of the model loop antenna. The antenna is swept in 10 KHz steps. The microprocessor is a SparkFun ESP32 "Thing". It drives a Si5351 clock generator. The initial testing was done with the raw square wave output. That seemed to work well, but for good measure the output is now filtered above 20 MHz. The 2nd harmonic is still present at low sweep frequencies (e.g., 6 to 9 MHz => 12 to 18 MHz). Still, it is a much cleaner signal with most harmonic content suppressed by 20 to 40 dB. I think I did the design with AADE Filter Design and Analysis, then I put the filter into National Instruments Multisim for further testing.
Power readings come from a AD8307 log amplifier and are sent to the ESP32 Analog ADC1-0, however, that channel conflicts with the Sparkfun Power Control Shield that will be used with the tuning motor. That will be resolved shortly.
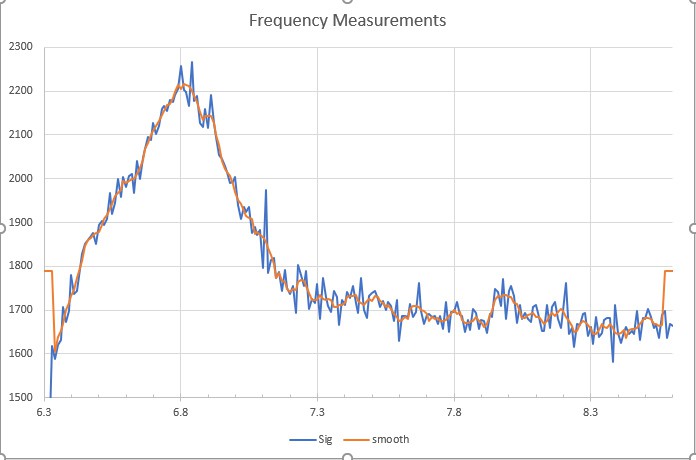
The jagged blue line is the raw data recorded by the ESP32. Units are byte value collect the the 10-bit A/D converter. I tested a variety of smoothing functions. I think this is a 5 point Savitzky-Golay filter. In the current version of the software, I first reduce the data set by selecting only data above the average of all the values. This sets the range for finding the peak. Then I use a 9-point Savitzky-Golay first derivative smooth. The peak is located with linear interpolation between values on either side of the zero crossing of the derivative. I will add a plot to show the peak finding later.
 Andrew Mitz
Andrew Mitz
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.