This project describes a joint hardware and software solution that delivers a 3D-display made from a rotating 2D panel. Depth is created by lighting the pixels at a precise time during a rotation and by using the viewer’s persistence of vision to generate animations in volume. The system is connected to a WiFi network, and can thus be used for displaying enriched types of content remotely.
System components
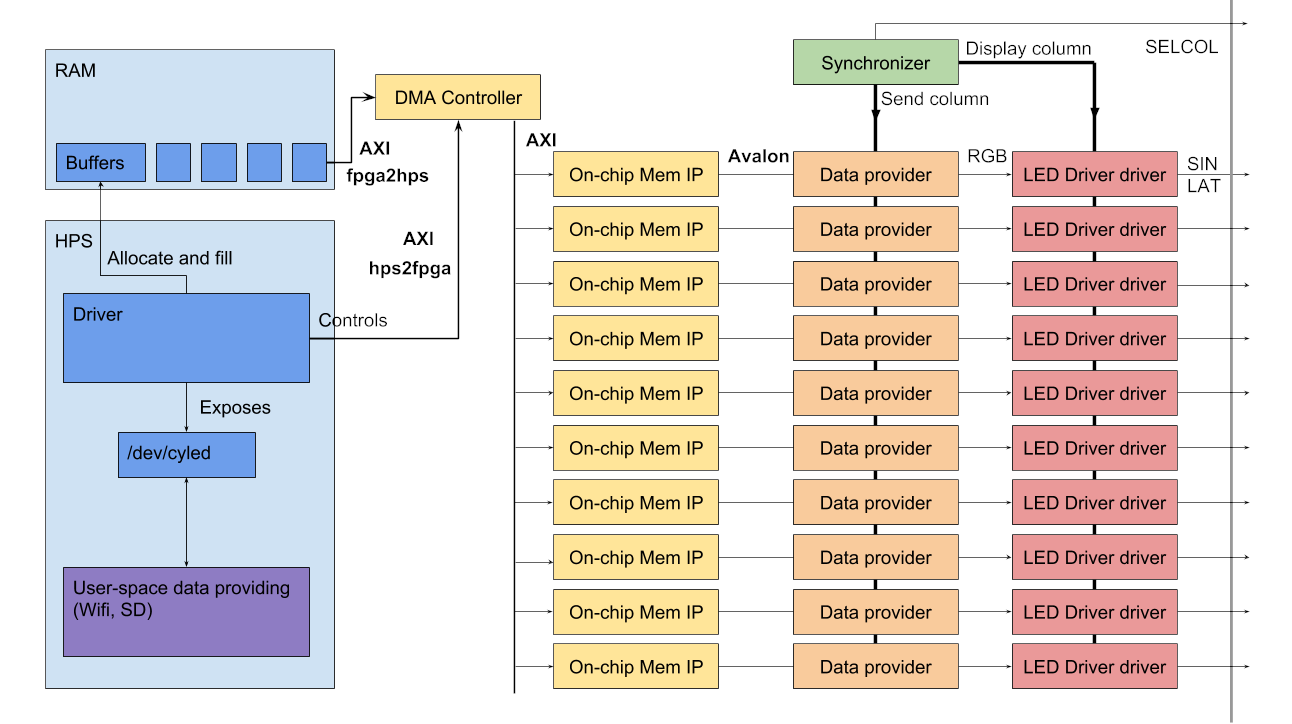
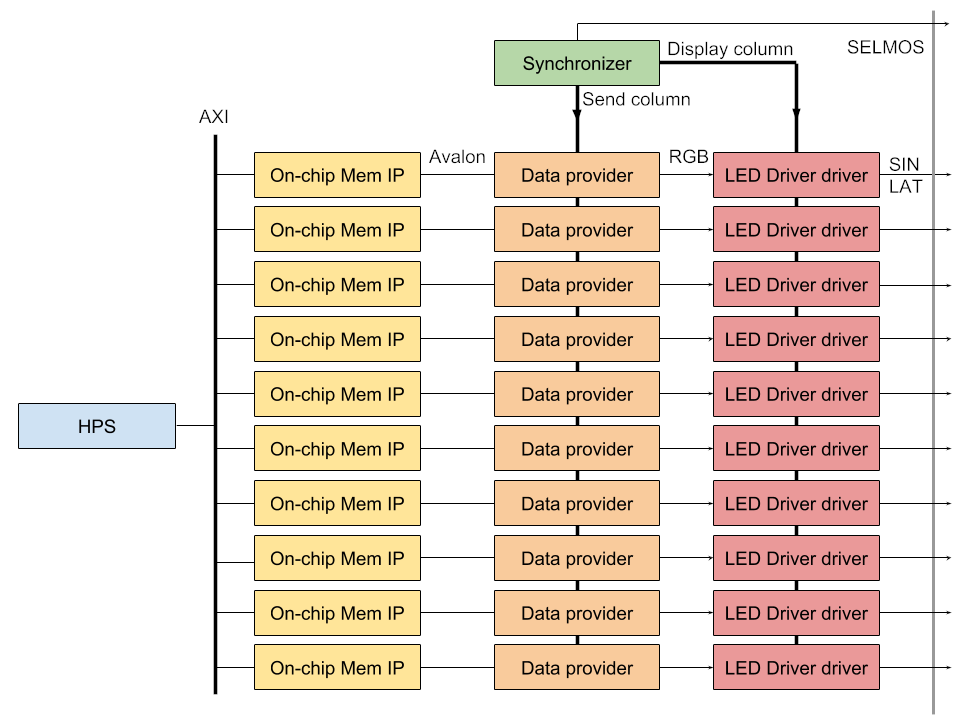
The main part of CyL3D is a rotating PCB. It features a 40x30 LED screen divided into 10 small areas of 15 rows and 8 columns. They are driven using a TI LED driver (TLC5957), which can drive up to 16 RGB LED, and is capable of receiving the next frame while displaying the current one. The 15 rows of each area are displayed simultaneously by each driver, and the 8 columns are multiplexed using a MOSFET (Vishay Si2333CDS) and a MOSFET driver (Renesas ISL55110). The main logic for sending frames to the drivers and multiplexing columns is implemented on an Intel Cyclone V FPGA. The system uses a magnet and a hall sensor to compute the rotation speed, and thus the correct rate at which to send frames, display frames, and change columns.
The actual data sent by the FPGA comes from an HPS (an ARM processor connected to an FPGA on the same die) running Linux. A custom kernel driver is used to exchange data between a user application and the FPGA. The user application can use any means to generate a 3D image. We made most of our tests using a simple application that can render text and images on a cylinder. But through a USB port with a WiFi dongle, we've also built an application to stream an animation from our laptops. This was a very important feature since, being a rotating screen, it was really the only way to display something without having to preload it first. (As a side note, the limit on the screen size came from the maximum throughput achievable using a rotating Wifi dongle). The rotating cube example was computed on a laptop and streamed to the platform in real-time.
Power management
The display is rotated by a brushless motor, powered separately from the rest of the electronics. A single 12V input is passed to the rotating element through the brushless motor (Turnigy Aerodrive SK3 - 4250-500kv Brushless Outrunner Motor). This 12V input is then converted to 2 different voltages: 5V for the LEDs and the WiFi dongle, and 3.3V for the System On Module containing the FPGA. The system is designed to power the LEDs up to 9A on the 5V rail, enough to give a clear rendering in a brightly lit room.
Features
As CyL3D is connected to a WiFi network, it is possible to directly control the device through a shell. Several commands are available, here are the most interesting ones:
- Testing: To test the driver and the display system
- Display settings: To change the general brightness of the display as well as the power given to each color. It is also possible to add a fixed angle to the image to align the front of 3D objects
- Display Text: Show a specific string on a specific cylinder slice of the system
- Display Time: Shows the current time on the screen
- Display Speed: Shows the current rotation speed of the rotating screen.
- Display Sphere: Draws a 3D sphere of given radius on the screen
- Display Droplets: Generates falling droplets on the screen to simulate a rain effect
- Display RAW: Loads a 3D model previously saved on the display system
- Display Streaming: The most interesting mode, which opens a TCP server to listen on. With the appropriate client, it is possible to live stream 2D and 3D animations to the display system over the network. In our case we had a client that was able to stream a 3D game of life simulation, as well as animated 3D models generated on Blender. Take a look at the videos below for demos! It would even be possible to use a 3D camera to capture a real-life 3D model, such as a face, adapt the data and retransmit it to the 3D display system, creating what we would...
 Alexis
Alexis













 Capt. Flatus O'Flaherty ☠
Capt. Flatus O'Flaherty ☠

 engunneer
engunneer
 Bryan Howard
Bryan Howard
This is incredible. I'm actually speechless at how awesome this project is