TimAs outlined earlier there are still two fast switching transistor types on the market: The PMBT/MMBT2369 and the BVS52. Both are offered by Nexperia and On Semi.
The PMBT2369 is Nexperias offer, my guess is that the "P" stands for Philips. Nexperia was carved out of NXP, which used to be Philips semiconductor branch. Similarily the "M" in MMBT2369 is most likely related to Motorola, which On Semi belonged to a long time ago. The BVS52 seems to be basically the same device at both vendors, so I did not bother investigating it.I compared On Semis and Nexperias flavors of the 2369. As you can see in the table above, their datasheet values are basically the same. I measured hfe and found the onsemi device to have slightly higher gain.
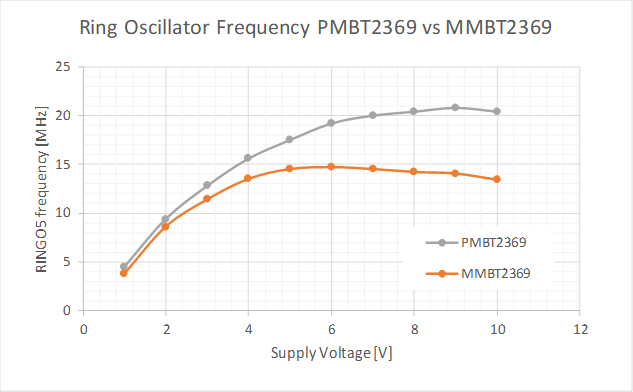
The plot above shows a comparison of both devices. It appears that the PMBT2369 is quite a bit faster. The MMBT2369 shows a maximum at around 5V supply. At higher voltage (current), the saturation charge seems to dominate switching behavior. This trend can only be seen at >8V for the PMBT2369.
Minimum tpd of the MMBT2369 based RTL inverter is 6.8 ns, that of the PMBT2369 based inverter is 4.8 ns.
It's quite difficult to asses the actual origin of the speed difference, just speculating: The higher current gain will increase the miller capacitance of the MMBT2369. However this is mostly relevant while the device is turned on. The critical condition is the storage time of the saturation charge, which flows out of the base when VBE is already zero and the miller capactance plays no role.
The PMBT2369 definitly appears to be the faster of the two. In fact, the PMBT2369 seems to be the fastest bipolar switching transistor that is still available in high volume today.
Why even look at other devices? Unfortunately it seems that the PMBT2369 is only available in the relatively large SOT23 package. To build dense discrete logic (yes, it makes no sense, I know), it would be of interest to use much smaller packages such as SOT523 or SOT723.
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
Interesting, what kind of models did you use? And simulator?
Are you sure? yes | no
What about PMST2369 in sot-323?
Are you sure? yes | no
Its the PMBT2369 in a smaller package. so it should be fine. havent tried it, though.
Are you sure? yes | no
btw, by parsing my spice models library I found that the BFP/BFR183 should ring at around 200MHz
Are you sure? yes | no
Not sure I understand correctly? But when you drive RF transistors into saturiation they usually get pretty slow.
Are you sure? yes | no
Simulations show that the PMBT2369 oscillates at 16.5 MHz. When I changed it to BFR183 it oscillates 208MHz@5V. perhaps he's "not enough RF" to slow down ;)
BFR182 oscillates at 68 MHz in the simulation.
BFP193: 98MHz
maybe the models is wrong, we just have to check...
Are you sure? yes | no
Better to check in a real circuit. The question is also if the transistor is driven in "logic mode". Its possible to get to some operating setting where the ring oscillator basically operates in small signal mode. It will oscillator pretty fast, but it's not really indicative of switching speeds.
e.g. see here:
https://hackaday.io/project/176107-led-coupled-logic-lcl
Are you sure? yes | no
this is clear. don't let him get saturated. Basics of ECL/CML.
Are you sure? yes | no
The point of the PMBT2369 is that you can let them saturate and they are still pretty fast. It's a special type of transistor (gold diffused/implanted) and apparently the last of its kind :)
Are you sure? yes | no
But all that said - it's quite possible that modern high end RF transistors are also pretty fast in switching. At least they like to oscillate a lot :). I haven't tried some of the newer SiGe ones in ring oscillators, only the trusty MMBTH10.
Are you sure? yes | no
all girls know that gold diffuses better on diamonds ;)
May we trust simulations? I see a clear correspondence between simulation and reality in the example of MMBT2369 and BC847C. And I really want to hope that the other curves are close to reality too...
https://ibb.co/9qzmqgX
Are you sure? yes | no
unfortunately twin brother PNP MMBT3640 is EOL since 2019
btw, are you sure about the quality of yours MMBTH10?
Are you sure? yes | no
I used original onsemi MMBTH10 (The first M is for Motorola, which onsemi spun off from)
btw, have you shared your simulation somewhere?
Are you sure? yes | no
You may see results here: https://ibb.co/6Bzynmg
Few more bjt's was added.
BC847 and MMBT2369 seem to match well your experimental data. but not MMBTH10
I have to reproduce your test setup ;)
Are you sure? yes | no
You made me curious, so I tried a more modern RF transitor:
https://hackaday.io/project/170697-evaluating-transistors-for-bipolar-logic-rtl/log/224820-ring-oscillator-with-rf-transistor-bfu520
:)
I believe the switching operation is simply not characterized and therefore not properly modeled in the spice models. RF guys usually want small signal S parameter models, they don't care about switching.
Are you sure? yes | no