The flyback converter finds many applications in DC-DC and rectifier designs. It can step voltage up or down, and can be built with and without isolation, and usually can be realized with low parts count. This section will give an overview of the theory of operation of the flyback converter, and the project logs will cover the design and build of the circuit.
This is the basic schematic for the flyback converter. I have exploded out the magnetizing inductance of the transformer as I find it helps understanding the current flow in transformer. This also shows why transformers don't work at DC: the magnetizing inductance will short out.
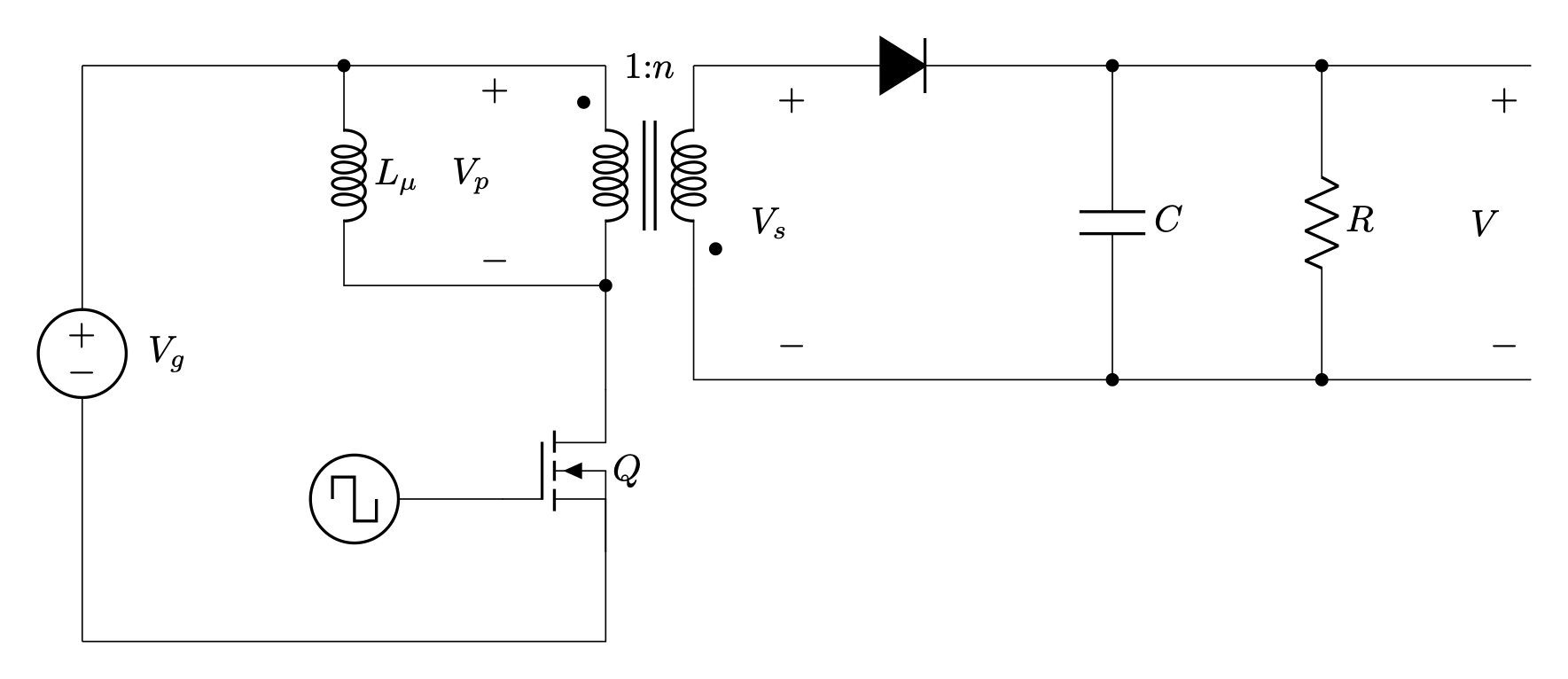
When the switch Q is on, essentially the entire source voltage Vg appears across the primary winding and magnetizing inductance. Since the transformer winding polarity is shown reversed, the secondary voltage is negative, and no secondary current can flow since the diode is reverse biased. Since there is no current flow on the secondary, all the current on the primary side is flowing through the magnetizing inductance. The capacitor C alone is supplying current to the load and is holding up the output voltage.
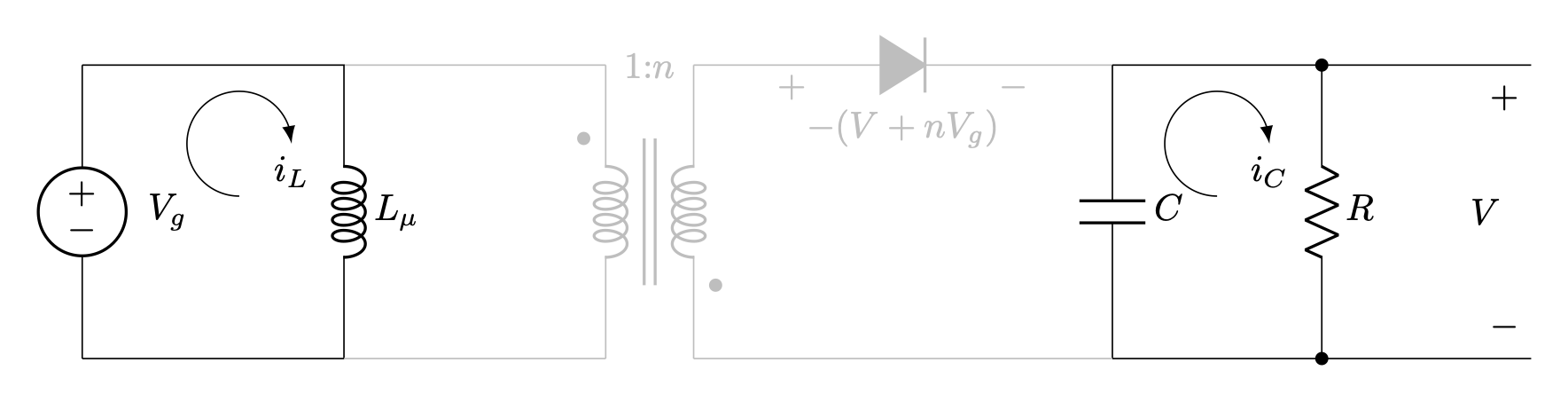
When the switch Q turns off, the current through the magnetizing inductance must continue to flow, so it will transfer to the secondary and forward bias the diode. Since the diode is on, the voltage at the secondary is V (+ the small diode junction voltage), and the voltage across the primary flips to -V/n. The secondary current charges the capacitor and also flows through the load. Also with the switch off, no current is supplied by the input source.
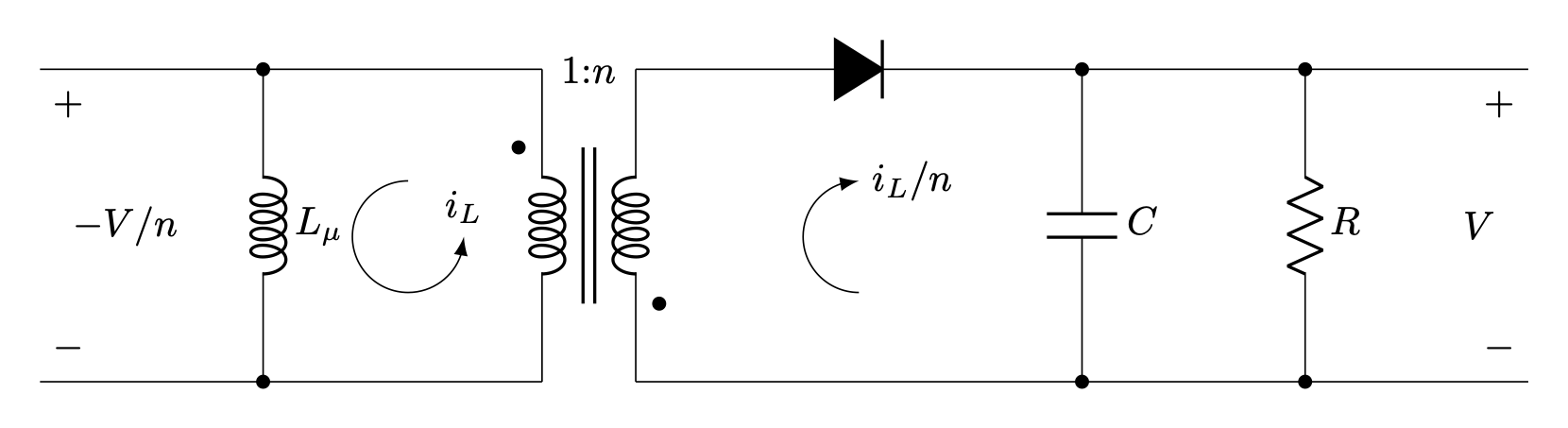
How do you analyze a circuit that rapidly switches between two distinct states? If the load remains constant, at some point, an equilibrium must be reached where the charge deposited on the capacitor during the switch-off state balances the charge withdrawn from it to supply the load current during the switch-on state. The output voltage will remain about constant, with some ripple up and down as the capacitor is charged or discharged. A similar principle applies to the inductance in the transformer. As the voltage across the magnetizing inductance flips signs, the flux linkage either expands or contracts. At equilibrium over the course of a switching cycle, the net change in flux linkage in the inductor is zero. These two principles, capacitor charge balance and inductor flux balance (sometimes called volt-second balance), lead to a steady state solution for both the average output voltage and inductor current.
The duty cycle D of a converter is defined the fraction of time the switch Q is on, with its complement D' = 1 -D as the time the switch is off. The average inductor voltage and capacitor current must be zero, leading to our equations of flux and charge balance:
The steady-state DC solution for the flyback converter as shown above is thus:
The formula for the duty cycle in terms of the input and output voltages is:
 James Wilson
James Wilson
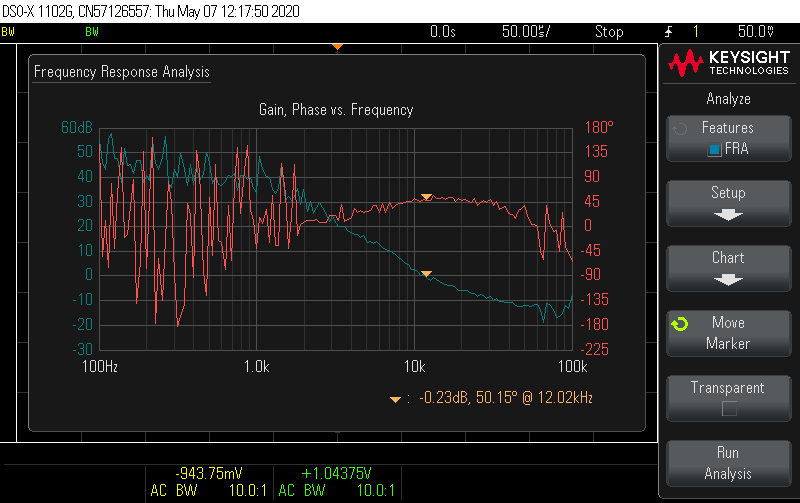


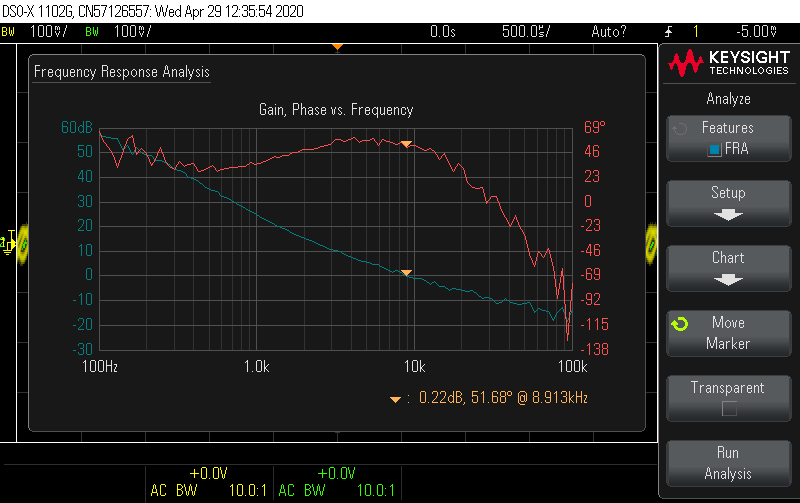


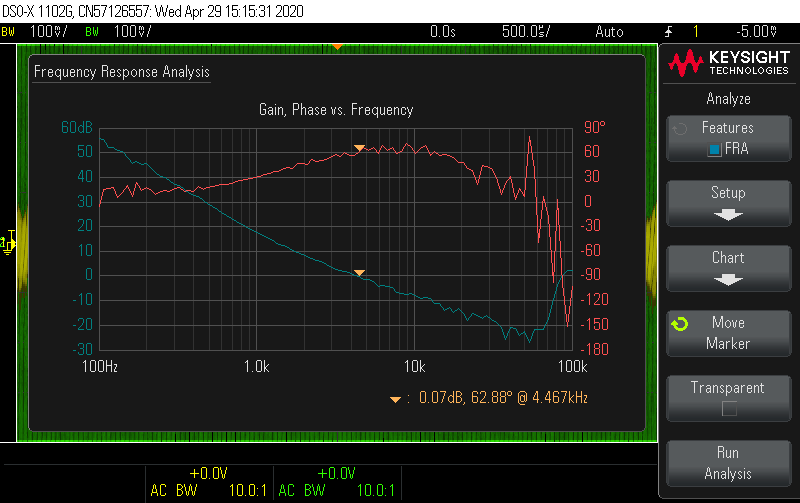


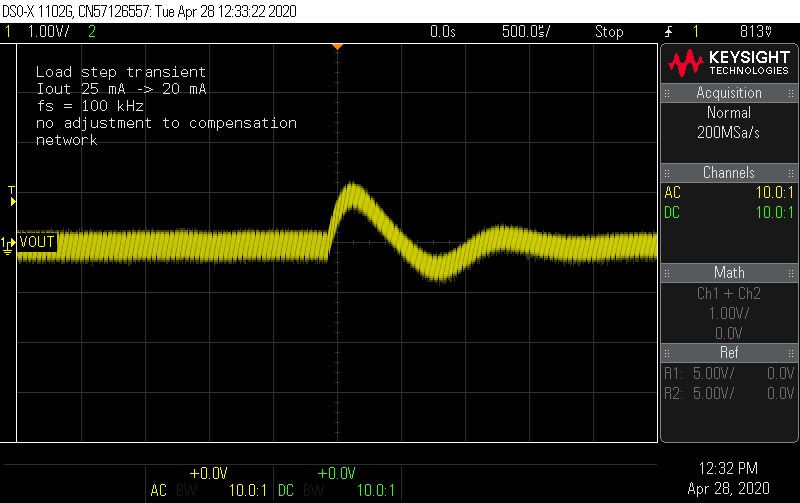

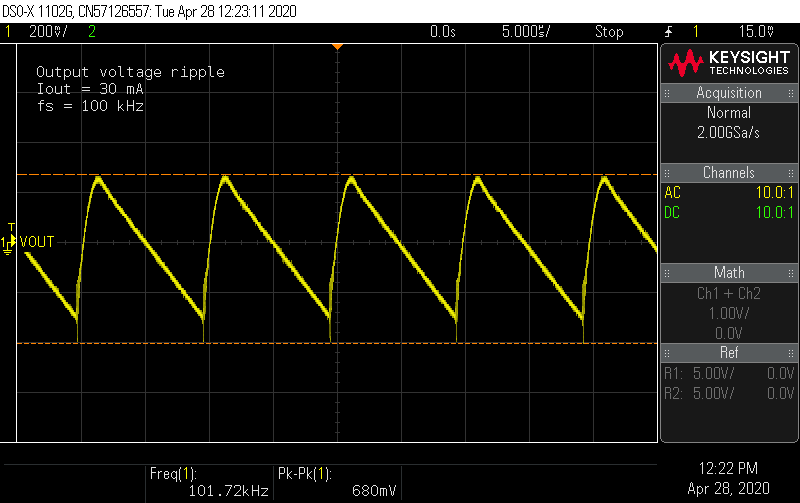
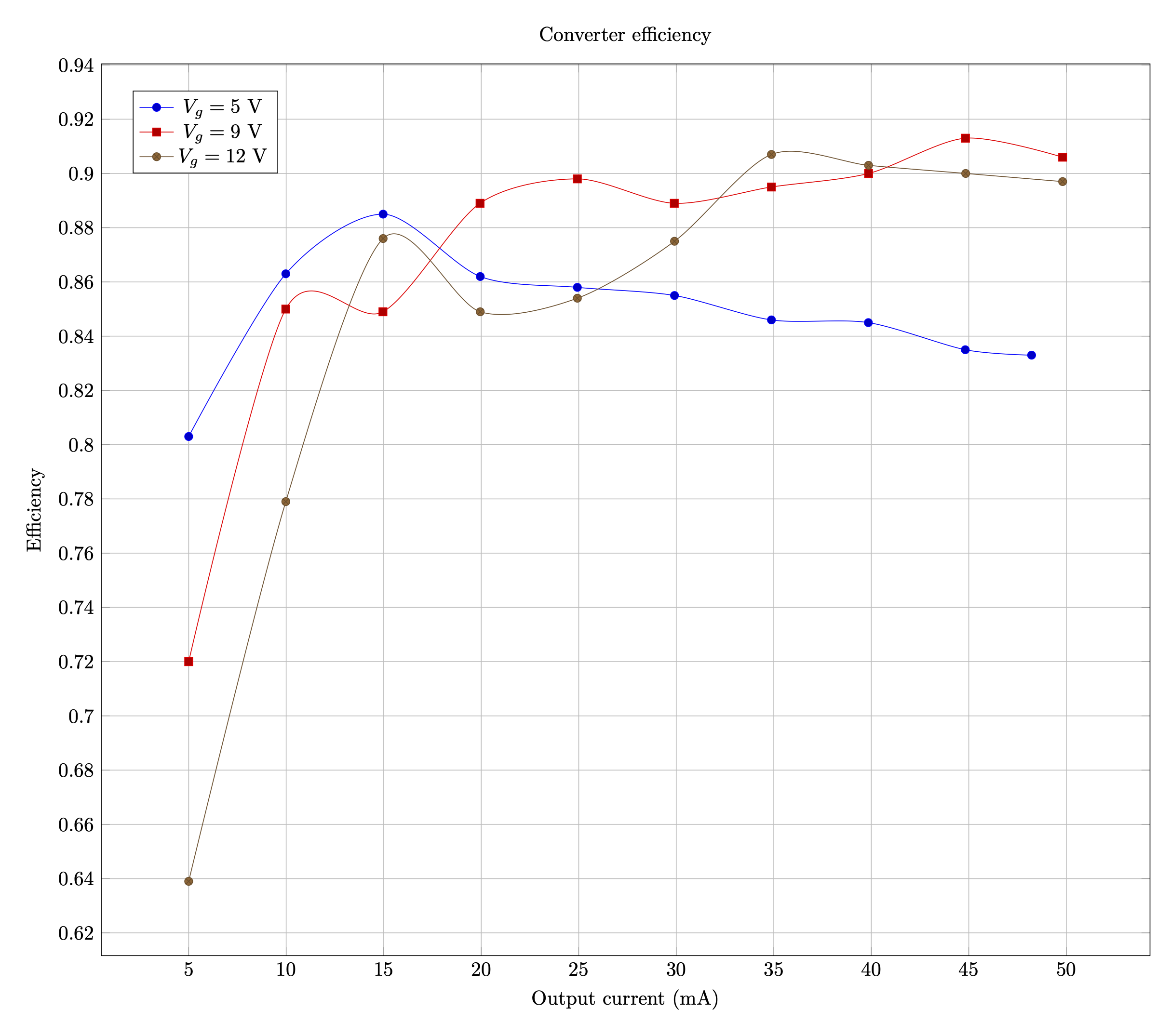
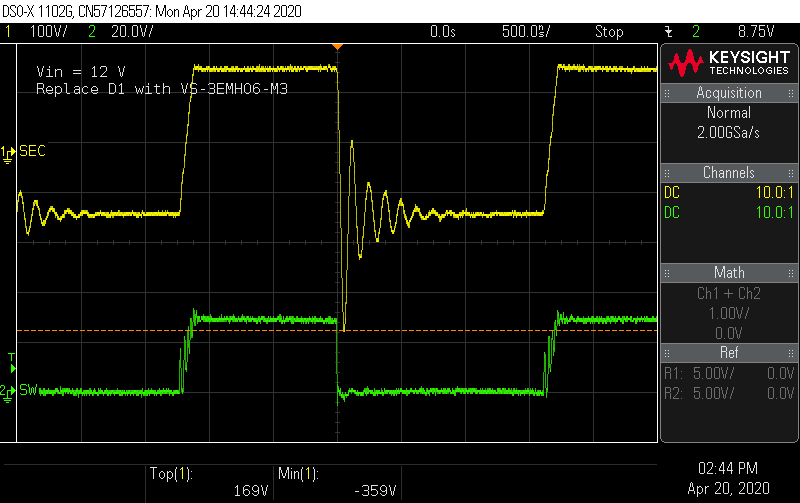
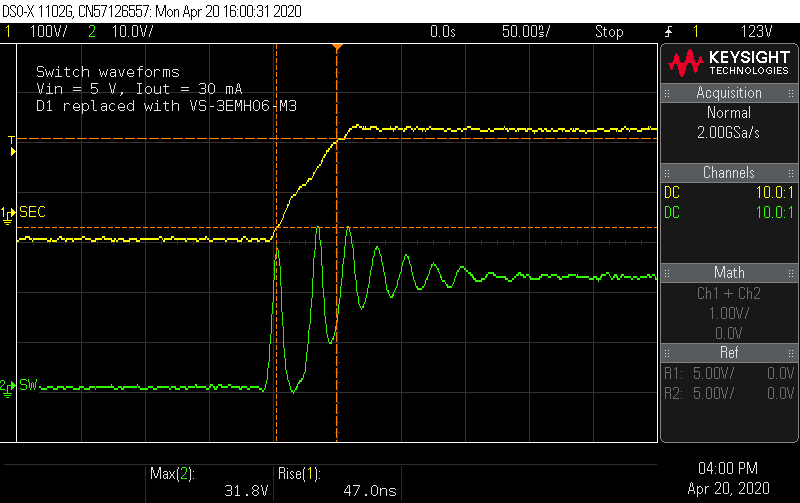 Probing the switch node shows a ringing waveform that looks much closer to the simulation. At the maximum inductor current condition, the voltage spikes are still 10% below the MOSFET Vds limit, without any snubber.
Probing the switch node shows a ringing waveform that looks much closer to the simulation. At the maximum inductor current condition, the voltage spikes are still 10% below the MOSFET Vds limit, without any snubber.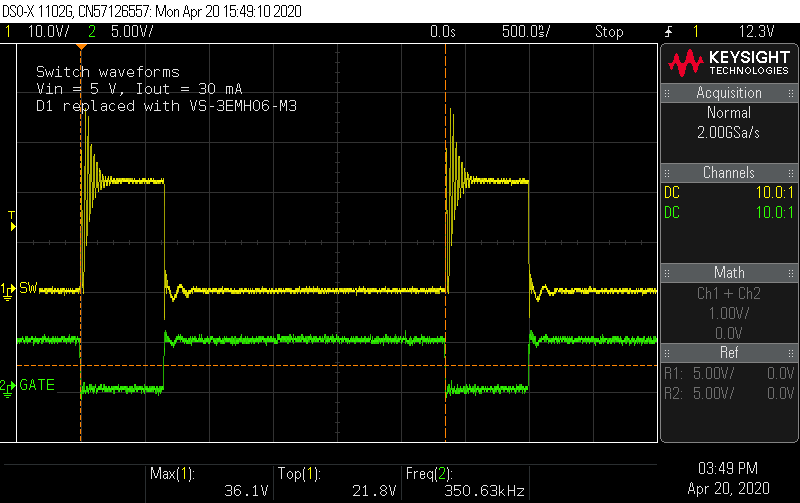






 Kuba Sunderland-Ober
Kuba Sunderland-Ober
 Paul Andrews
Paul Andrews
 Krists
Krists
 Bud Bennett
Bud Bennett
Hi!
It was a pleasure to read and follow each step of project, very professional approach to the matter. As I`m newbie at power supply for Nixie clock project, my question might sound silly, I wonder why at board schematics I see transformer`s dot of second coil tied to GND (corresponds to pin 1 of DA2032-AL), but on PCB design this pin is tied to HV output. Pins are swapped. Need some explanation. Thanks!