-
Initial parts selection
04/16/2020 at 01:32 • 1 commentWhile most parts will be chosen downstream of design decisions, several other parts will need to be chosen early and will drive other design decisions. The big parts we need to sort out first are the controller, the transformer, the MOSFET switch, and the diode.
---------- more ----------The controller
As noted in the project brief, one reason I took up this project was to design something with the LM5155, a new boost/flyback/SEPIC controller that TI started offering in 2019. From my standpoint, it offers a number of improvements over the controller I used for a previous DCM boost controller, the LM3478. Several of the datasheet figures regarding the current-programmed mode threshold are a lot tighter on the LM5155. The soft-start feature of the LM5155 is adjustable and easy to design around. The LM5155 also supports a wider switching frequency range and very low voltage operation, though I won't be pushing either of those limits.
The transformer
Based on the formulas for the flyback converter output voltage, the turns ratio of the transformer has a big impact on the voltage conversion ratio. This is good because we can get a large conversion ratio without an excessively high duty cycle, and the LM5155 has a upper limit on the duty cycle of about 85-90%.
The transformer will also put an upper bound on the amount of output current the converter can support. From the formula on inductor current, the average inductor current is n/D' times the load current. The actual inductor current ramps up and down over the switching cycle, often significantly, so we need to pay attention to the peak current and keep the transformer core from saturating. The combination of the inductor current ripple, and the limits of the transformer will also drive the choice of a switching frequency.
There are only a few commercially available transformers that have a high turns ratio (n = 10), can support a high secondary voltage, and support decent amounts of the current. These transformers were built specifically for the LT3750 high voltage capacitor charger circuit, which is pretty close to our application, but is designed around applications where the capacitors are discharged almost instantly -- think of a camera flash. The suitable transformers I found were:
- Coilcraft DA203x series: DA2032, DA2033, DA2034
- Wurth WE-FB series: 750032050, 750032051, 750032052
For now, I want the converter to support up to a 30 mA output current, which ought to be enough to drive 10 smaller Nixie tubes with room to spare. Lower input voltage means higher currents, so the maximum current will be seen at the lowest input voltage, which I decided to put at 5 V.
Using the formulas at the end of the details section, at 5 V input and 30 mA output with n=10 turns ratio, D = 0.773 and IL = 1.32 A. If we allow up to a 50% current ripple, the peak current is 1.98 A, so for some headroom, something rated for about 3 A is good.
The DA2032 fits this spec exactly. The Wurth transformers do not list saturation current, but given the physically similar size, it's probably close to the Coilcraft part. The 750032050 has nearly identical specs to the DA2032 (price, inductance, DC resistance, and leakage inductance). The 750032051 has lower leakage inductance -- more on why this is important later -- but it's quite expensive. Unfortunately, none of these have compatible component footprints, and they are too large to place all on one board to pick and choose later, so I committed to the DA2032 since it meets the requirements and is low cost.
The MOSFET
One advantage of the flyback topology, compared to the boost converter, is that the switch doesn't need to block the full output voltage, so a lower-voltage, higher-performance part can be used. High performance, for a MOSFET, means lower on-resistance or Rds(on), and lower gate charge and capacitance (Qg). The Vds figure needs to withstand the off-state voltage of Vg + V/n, as seen in the diagram in the details section. With a maximum design input voltage of 12 V, and an output voltage of 170 V, and the 1:10 transformer, the MOSFET needs to be able to block 29 V. Some headroom is required, because between the leakage inductance of the transformer, and the output capacitance of the MOSFET, there will be ringing and overshoot when the switch turns off, unless attenuated by a snubber, and this can damage the MOSFET if the peaks exceed its Vds limit. The ringing is actually worse at lower input voltages, since it starts with the energy in the leakage inductance that is built up during the on-stage. The energy in an inductor is proportional the square of the current, which is higher at lower input voltages.
MOSFET technology continues to advance, and some of the latest and greatest switches are in Infineon's OptiMOS 6 lineup. These parts offer Rds(on) figures below 6 mΩ, and some Qg figures below 10 nC, though they are presently limited to 40 V. While it is tempting to pick the lowest Rds(on), I prefer to minimize the Qg figure at the highest Rds(on) I can tolerate, to get cleaner waveforms and have less agressive snubber circuits. For this reason, I chose the 5.9 mΩ/9.4 nC part, the BSC059N04LS6. The "BSC" is actually the larger of two packages available, but for an evaluation board, I prefer a larger part (easier to rework and probe) and there's always the option to miniaturize for a more mature board later.
The diode
While the MOSFET gets off easy, from the on-state diagram in the details section, the diode is reversed biased with a voltage of (V + n*Vg). When Vg = 12, the diode has to block 290 V! While Schottky diodes are usually the first choice in switched-mode power supplies, they are limited to lower voltages (< 200 V), so we'll need to choose a super-fast rectifier with at least a 400 V rating and deal with any consequences of diode reverse-recovery. Since the peak inductor current at the primary is about 2 A, the secondary current should not exceed 200 mA, and a 1 A rated diode should suffice. The fastest diode series I found was the ES1 series, offered by several manufacturers. The ES1G is the 400 V part, and I chose the version from ON Semi in the familiar SMA/DO-214 package.
-
Datasheet design parts
04/16/2020 at 06:07 • 0 commentsNow that the controller chip has been chosen, there are a lot parts to pick based on datasheet requirements. Most of these choices are straightforward, but some, such as the choice of switching frequency, need some consideration of the limits of other parts choices, and the compensation components, which will require extensive theoretical development or some intuition coupled with experimental evaluation.
---------- more ----------Converter design parameters
- Input voltage: 5 to 12 V
- Output voltage: 170 V
- Maximum output current: 30 mA
Switching frequency
The way I picked the switching frequency was to work backwards from the maximum inductor current ripple limit. The results in the details section rely on the idea that the average inductor current can be substituted for the time-varying result. If this assumption, called the small-ripple approximation, is no longer true, than more complicated mathematics must be applied, as is the case when the inductor current goes to zero during the switching cycle, and the converter is said to be operating in discontinuous conduction mode (DCM).
During the on-state of the switching cycle, the voltage applied from the input source ramps the current in the inductor. For an inductor, v = L (di/dt), so the slope of this ramp is v/L. The peak-to-peak ripple is this slope times the amount of time the switch is on and this voltage is applied:
Solving for the switching frequency (reciprocal of the period T):
The maximum duty cycle and current occur at the lowest input voltage (5 V). The computed duty cycle and inductor current are D=.773 and IL = 1.4 A. I'd like to keep the ripple to less than 40% of the average current, so plugging values in, the resulting switching frequency is 366 kHz. I rounded this to 350 kHz and used the timing resistor formula in the LM5155 datasheet to obtain a timing resistance of 62 kΩ.
Feedback resistors
The voltage reference on the LM5155 is an even 1 V, so I need to reduce the output voltage of 170 V to 1 V, preferably without burning much current since this converter is designed to supply 30 mA. As luck would have it, there is an E96 value combo that gives us an exact 1/170 resistor divider and draws less than 1 mA at 170 V: use a 1.69 MΩ & 10 kΩ divider.
Undervoltage lockout (UVLO)
The LM5155 has a feature to adjust the UVLO levels that shutdown the converter, with configurable hysteresis. This isn't important for an evaluation board that will checked out on the bench, but I decided to set an on value of 4.75 V and off value of 4.6 V. The datasheet has a formula to set the resistor divider on the UVLO pin, which yields R1 (top) = 18.7 kΩ and R2 (bottom) = 8.66 kΩ - these are rounded to the closest E96 values.
Soft start
The soft start circuit in the LM5155 charges the voltage reference using a 10 µA current source into the attached external capacitor. Once the voltage on the SS pin hits 1 V, the internal voltage reference takes over, so the soft start time is determined by the time it takes to charge the capacitor to 1 V, so 10 nF gives a startup ramp time of 1 ms. I don't consider this critical for a evaluation board powered by a bench power supply, and some datasheet examples used 22 nF, so I picked this as a starting point.
Current sense network
This section relies on results from the theory of current programmed control that are not immediately obvious. An excellent reference on current programmed mode is chapter 12 of Fundamentals of Power Electronics by Erickson and Maksimović.
The LM5155 uses peak current control (also called current programmed mode) to set the duty cycle. This offers overcurrent protection and also improves the stability of the feedback loop. The inductor current is sensed by observing the voltage at a low-side shunt resistor. When the voltage level at the CS pin hits the controller's threshold, the MOSFET turns off for the rest of the switching cycle.
![]()
According to the control theory of the current programmed mode, there is an inherent instability when the resulting duty cycle > 1/2. To fix this problem, an artificial ramp is added to the sensed current (or equivalently, the ramp is subtracted from the threshold limit). The same result requires the slope of artificial ramp to be at least half the slope of the inductor current in the off-state. From the off-state diagram in the details section, the off-state voltage across the magnetizing inductance is -V/n, so the magnitude of the off-state current slope is V/(n*L). The requirement for the artificial ramp can be expressed like this:
Here Rs (the sensor resistor) is included since all currents are observed relative to the sense resistor. The LM5155 datasheet doesn't state the artificial ramp slope, but it gives the amplitude of the voltage ramp, which is 40 mV. As slope = rise / run, the right hand side can be replaced with the magnitude of the ramp divided by the period of a switching cycle (or multiplied by the switching frequency):
This places a limit on the sense resistor to achieve stability. Plugging in the values from the datasheet and the design so far, Rs must be less than 16 mΩ. Derating this value by 20% as recommended in the datasheet yields Rs < 14 mΩ. On the other hand, when the peak inductor current hits the threshold,
The DA2032 transformer's saturation current is 3 A, so the required sense resistor is 33 mΩ.
Is all hope lost? No! By adding a series resistor to the CS pin, additional artificial ramp can be added. An internal 30 µA current source drives a voltage ramp across this series resistance. To find the right values for the sense resistor and slope resistor, two equations must be solved simultaneously for Rs and RSL:
In the above, beta is the slope factor, which the datasheet recommends using 0.82 (recall 0.5 is the minimum for stability). Solving for the same maximum current condition yields Rs = 18 mΩ and RSL = 1 kΩ.
Additionally, the LM5155 datasheet recommends a low-pass filter on the CS pin. They state this design recommendation for the RC filter:
All this means is that when the sensed current drops to zero in the off-state, the filter should get at least 3 x the filter time constant to discharge the capacitor. Additionally, it makes sense to have R be small compared to RSL since it appears in series with it. I picked R = 20 Ω, which requires C < 11 nF at the maximum duty cycle of .773. I chose C = 4.7 nF for an extra margin.
-
Picking input and output capacitance
04/17/2020 at 06:21 • 0 commentsThe capacitance added at the input and output of the converter will impact the voltage ripple.
Output capacitance
There are some different ways to choose the output capacitance. One approach is determine the voltage ripple of the converter, and solve for the capacitance needed to meet the ripple spec. From the circuit diagram in the details section, the capacitor discharges during the on state. Using the small ripple approximation that the current is about constant during this interval, the voltage ripple can be expressed as
Solving for C:
Nixie tubes don't need perfect DC, so a peak-to-peak ripple of 1 V is more than sufficient. Under the target load of 30 mA and the maximum duty cycle at 5 V input of .773, the required output capacitance is 66 nF.
---------- more ----------Another way to pick output capacitance is by the desired load transient over/undershoot. When output current jumps, the output voltage briefly drops before the feedback loop returns things to regulation. How sharply the voltage undershoots is a function of both the output capacitance and the bandwidth of the feedback loop.
A crude way to estimate the load transient is to observe that below the crossover frequency, the feedback loop reduces the effective output impedance of the converter, and at high frequencies, the output impedance of the converter is also low because of the output capacitance. The converter's output impedance is likely at a maximum near the crossover frequency, and this can be used to estimate the magnitude of the load transient:
Skipping ahead to the results of the compensation section I'll talk about soon, I ended up picking 8 kHz as the crossover frequency. Let's say I want to keep the voltage undershoot to 1 V when the load goes from 50% to 100% (15 mA to 30 mA). The required output capacitance from this formula is 298 nF.
I ended up using the latter method and rounded this up to 2 x 220 nF capacitors with a 10 nF ceramic capacitor to handle very high frequency transients. The larger capacitors are film type for their low ESR/dissipation factor and high voltage ratings. In this capacitance, film capacitors are available using either PP or PET plastic. PP has superior dissipation factor, but I'm not sure it matters for this application, so I picked a package where I could try both.
Input capacitance
One way to size the input capacitance is to imagine the input capacitor alone supplies current to the inductor during the on-state, and gets recharged instantly when the switch turns off. How much capacitance would be needed to meet the desired ripple spec? The voltage ripple of a capacitor sourcing the average inductor current during the on period is:
I want the input voltage to drop no more than 1% or 50 mV. Using the maximum current and duty cycle conditions (Vg = 5 V, D = .773, IL = 1.4 A), then the required input capacitance is 62 µF. I rounded this up to 2 x 47 µF aluminum poly bulk capacitors. In addition, a few ceramic 10 µF or smaller caps will help reduce high frequency spikes.
-
Closing the feedback loop
04/18/2020 at 02:21 • 0 commentsA converter needs a feedback mechanism to maintain voltage regulation. The choice of a duty cycle only works for a particular set of load resistance and input voltage. Variations, large and small, need to be corrected to maintain a stable output voltage level. Feedback loops are fickle things, and unless carefully constructed, can become unstable. Stabilizing the feedback loop is the purpose of the compensation components attached to the controller chip.
There are few ways to determine how to compensate the loop, generally it's either relying on some intuition (or cribbing from something known to work) and then experimentally verifying it, or it's deriving an analytical model of the converter's feedback loop and solving for the optimal component values. I'm going to try to do the latter in this log. Unfortunately, the derivation alone can take pages, even with a background in control theory, so I'm unsure how much to document. I can always add detail on request.
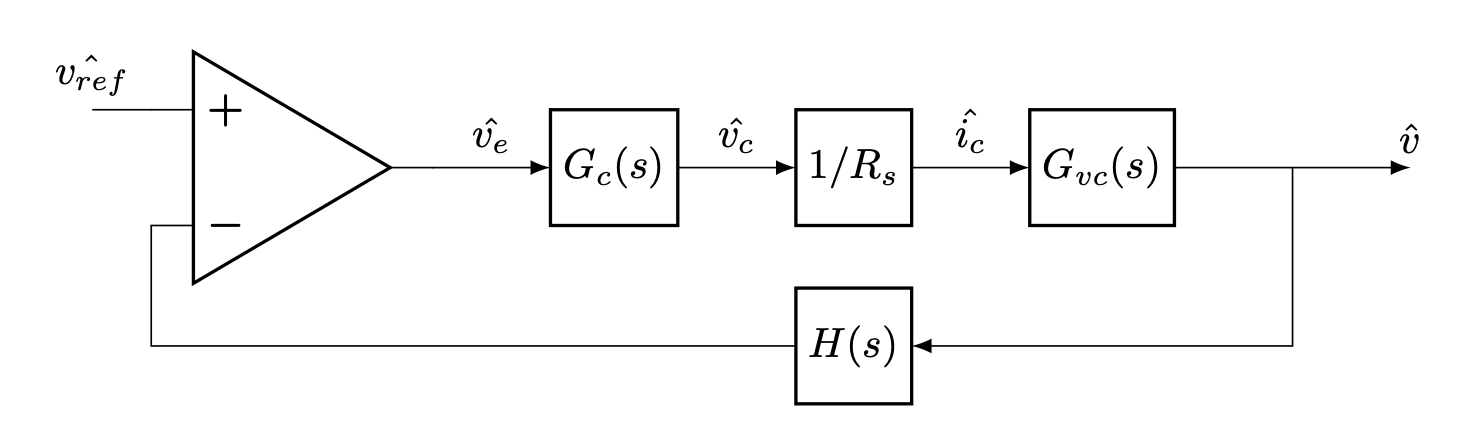
The LM5155 control loop
This is a simplified view of the control loop of the LM5155. The "hat" notation refers to small-signal variation, i.e. a linearized model of how the system behaves when values are perturbed from their normal DC operating point.
---------- more ----------![]()
Starting on the right, the output voltage is passed through the sensor block H. This is just a resistor divider with a gain of 1/170 for this converter. This is subtracted from the LM5155 voltage reference, creating an error signal. The error signal is fed through the compensation network, and then voltage is converted to a current value by the resistance of the sense resistor. The resulting current control signal is fed into the current programmed controller and the current-to-output gain Gvc determines the feedback output voltage. Determining the structure of Gvc (all its poles and zeros) is the hard work of the analytical path.
Current mode controllers generally need a simple compensation network, called a type II compensator, that is just a shunt resistor and capacitor in series. This has an origin pole and a zero at the RC corner frequency. An optional high frequency pole is added by putting another capacitor in parallel with the series branch.
![]()
To determine Gvc, the first step is derive a small-signal AC model of the converter. This can be obtained through my preferred method of state-space averaging, or by circuit analysis using an averaged switch model.
![]()
From the small signal model, the control-to-output-voltage and control-to-inductor-current transfer functions can be solved from the state-space analysis results or read off the AC small-signal circuit. These are voltage mode transfer functions though, and what's needed is the current mode control-to-output-voltage transfer function. Converting them requires parameters of the current mode modulator (why I said that a large artificial ramp affects the stability of the system). Sounds like a lot of work? It is.
For the flyback converter, the current-mode control to output transfer function can be written in the form:
This means there a DC gain Gc0, a single real zero in the right hand plane, and a pair of resonant poles. In the following, L is the transformer magnetizing inductance, C is the output capacitance, and R is load resistance. These are:
The modulator parameters are:
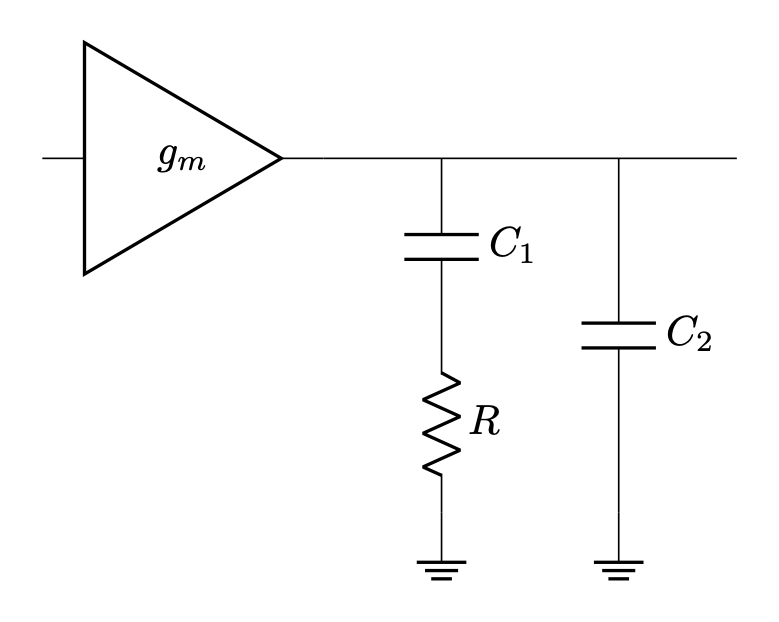
Choosing the compensation network
With that out of the way, how to actually get those magic R and C values? For stability, it's important to design around the right hand plane zero in the transfer function. A way to understand a right hand plane zero is to imagine a car that, when you tap the brakes, very briefly speeds up before slowing down. If that blip of speed happens and is over before you can notice and react, all is fine. But if you do have time to notice, you panic, hit the brakes harder, which makes the car speed up again ...
To prevent this situation in this power converter, the control loop bandwidth needs to be significantly lower than the RHP zero frequency, so the loop will not try to correct for it. Using the parameters for the converter that will yield the lowest frequency (5 V input, pushed to 40 mA output just for headroom), the RHP zero frequency is 45 kHz. To meet this criterion, the crossover frequency (where the gain of the feedback loop is 0 dB) is usually kept below 1/5 the RHP zero frequency. In this case, I rounded it to 8 kHz as the target crossover frequency.
Another requirement for stability is the phase margin criterion. This says that a system is stable if, at the crossover frequency, the system's phase is greater than -180°. The difference between the system's phase at crossover and -180° is the phase margin, and typically a figure of around 60° is a good target.
The choice of the compensation resistor will adjust the gain at crossover, and the zero from the RC corner frequency will give some control over the phase. One can figure out the ratio of the uncompensated gain at crossover, determine the gain adjustment required to hit 0 dB, scaled by the LM5155's amplifier transconductance ... meh, just give the job to a computer, it will happily descend gradients for you and nail both the crossover frequency and phase margin. I wrote a python script that uses scipy's optimize framework to iteratively select the exact values. I also added the optional high-frequency pole in this script - the choice of frequency is arbitrary, but placing the HF pole at the RHP zero frequency is one choice.
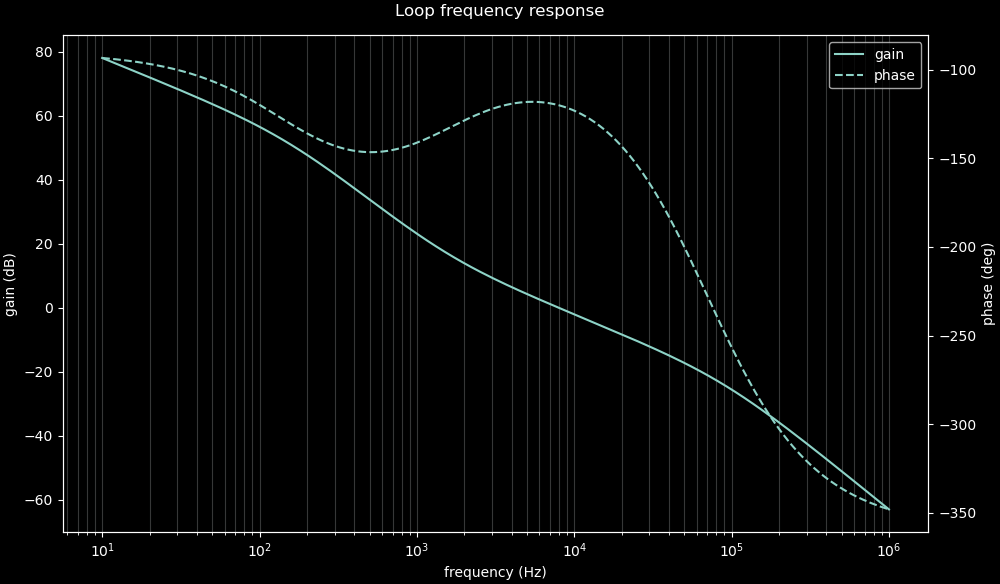
Here's the output of the script:
Type II OTA compensator Compensation network for crossover at 8000 Hz with 60° phase margin: R_c = 1504.96 Ω, C_c1 = 6.87088e-08 F, C_c2 = 1.80016e-09 F Chosen compensation network: R_c = 1.5e+03 Ω, C_c1 = 6.8e-08 F, C_c2 = 1.8e-09 F Crossover at 8e+03 Hz, phase margin: 60°
So that's the network I'll use: R = 1.5 kΩ, C1 = 68 nF, and C2 = 1.8 nF. The script also plots the Bode chart of the compensated feedback loop. Edit: I later found my script left out the PWM gain factor. The correct numbers for this configuration are R = 11 kΩ, C1 = 10 nF, and C2 = 270 pF.
![]()
Experimental validation of the loop gain
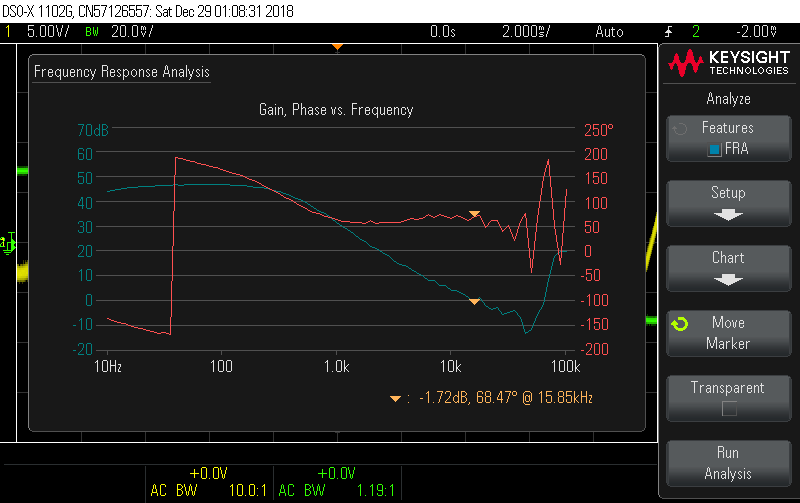
Sophisticated mathematical models are one thing, but useless if you can't validate them. One method to analyze the feedback loop in circuit is by injecting a voltage signal into the feedback line using a function generator and observing how that signal is coupled to the output. My oscilloscope (Keysight 1102-G) has a frequency response analysis tool that produces a Bode chart similar to above by comparing the voltages at both channels as the function generator sweeps through a frequency range. If it works right, the plot will look something like this, taken from an older project.
![]()
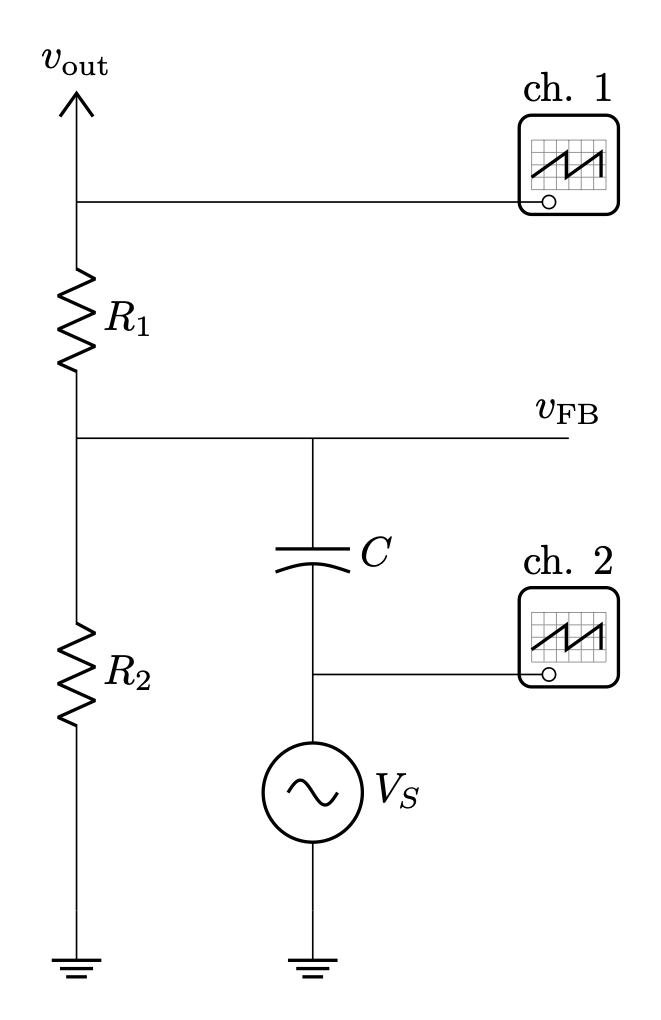
To do this, the signal has to be injected without disturbing the DC value of the feedback line. Here is the sketch of a voltage injection circuit that doesn't break the feedback loop.
![]()
At DC, the feedback voltage is just the output voltage scaled by the resistor divider. The capacitor C is large, say 1000 µF, and can be thought of as a short at any frequency above DC. The source generator VS is a typical function generator with 50 Ω impedance. The total impedance of this branch should be small in comparison to R2 (10 kΩ in the design), which means the DC level of FB is unchanged, but the AC component is almost entirely driven by the function generator. Probes connected to the output voltage and the output of the function generator should be tied to the same ground point, and then the frequency response analysis tool can be started. Because of the high gain of the error amplifier in the LM5155, the voltage level required from VS is very small, and can be more precisely set by coupling VS across a 1/1000 resistor divider.
In the board design, a pair of headers allows the attachment of a function generator, labeled J5 and J6 on the board.
-
Simulation
04/18/2020 at 19:48 • 0 commentsWith components selected, it's time to move toward realizing this converter. The next step will be testing the design in a circuit simulator.
People like to gripe about LTspice's outdated UI, but I've gotten pretty fast at sketching up circuits with it. Unfortunately, the LM5155 SPICE model is encrypted and only works in TI's SPICE variant, TINA-TI. TINA-TI is free to download and use, but LTspice is in many ways leagues better. Want to peek at some node voltage? In LTspice, just click on the node in the schematic after the simulation is done. In TINA-TI, the transient simulation only records voltages and currents for explicitly added meters, so that means adding a meter and re-running the simulation.
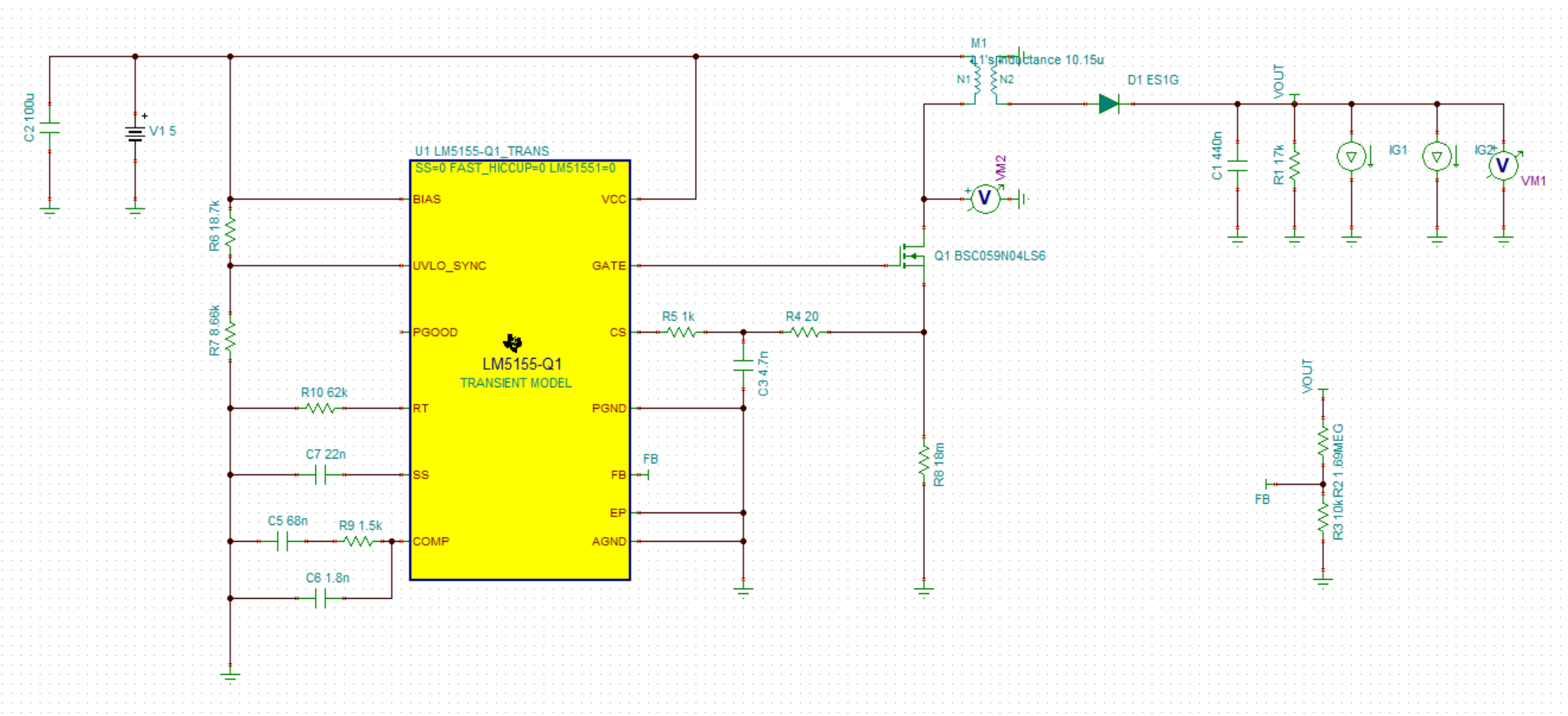
---------- more ----------Here's the converter schematic in TINA-TI:
![]() I changed the initial load to 11.33k to get a 15 mA output current and added time-delayed step current sources IG1 and IG2 to simulate a load step-up and step-down of 15 mA. Here's the output voltage plot, showing the startup ramp and load step at 5 ms/6 ms:
I changed the initial load to 11.33k to get a 15 mA output current and added time-delayed step current sources IG1 and IG2 to simulate a load step-up and step-down of 15 mA. Here's the output voltage plot, showing the startup ramp and load step at 5 ms/6 ms:![]() Close-up of the load step transient shows the transient is larger than 1 V as predicted by formula used to pick the output capacitance, but it seems acceptable for the application. The converter returns to regulation within a millisecond and shows good stability.
Close-up of the load step transient shows the transient is larger than 1 V as predicted by formula used to pick the output capacitance, but it seems acceptable for the application. The converter returns to regulation within a millisecond and shows good stability.![]() Looking at the switch node or MOSFET drain at full load, there's a problem: the voltage is spiking above 40 V and will need a snubber.
Looking at the switch node or MOSFET drain at full load, there's a problem: the voltage is spiking above 40 V and will need a snubber.![]()
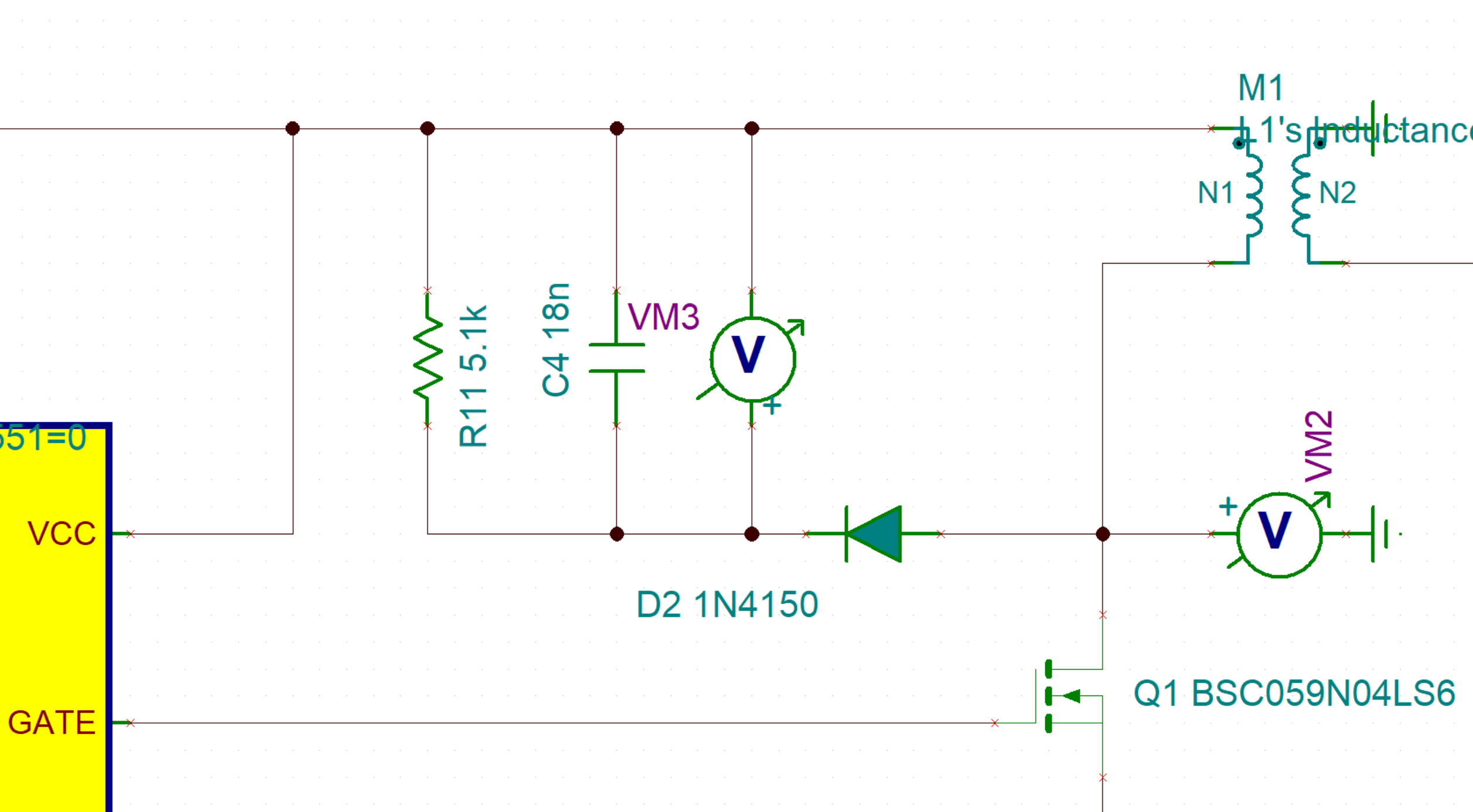
To build the snubber circuit, I turned to application note from Fairchild Semiconductor, AN 4147, that describes how to design a RCD snubber for a flyback converter. Even though it has "RC" in the name, the RCD snubber is nothing like a RC snubber that tries to damp resonance through matching the characteristic impedance of the parasitic elements. I spent a lot of time trying to understand this circuit before I realized it's actually similar to a boost converter that's driven by the resonance between the leakage inductance and MOSFET output capacitance, instead of a PWM gate driver, making it a kind of resonant converter! In this case, I selected a snubber voltage of 32 V or 80% of the MOSFET's rating, and the design equations in AN 4147 yielded R = 5.1 kΩ and C = 18 nF. I picked 1N4150 as the diode, it's rated to 50 or 75 V depending on the particular manufacturer, and is quite fast. This is the snubber circuit added in the simulation:
![]() The simulation with this circuit added shows the switch node voltage gets clamped at 32 V as predicted. There's still a lot of ringing, but the goal of protecting the MOSFET has been achieved. Snubbers always need experimental verification and tuning, but this looks like a promising starting point.
The simulation with this circuit added shows the switch node voltage gets clamped at 32 V as predicted. There's still a lot of ringing, but the goal of protecting the MOSFET has been achieved. Snubbers always need experimental verification and tuning, but this looks like a promising starting point.![]()
-
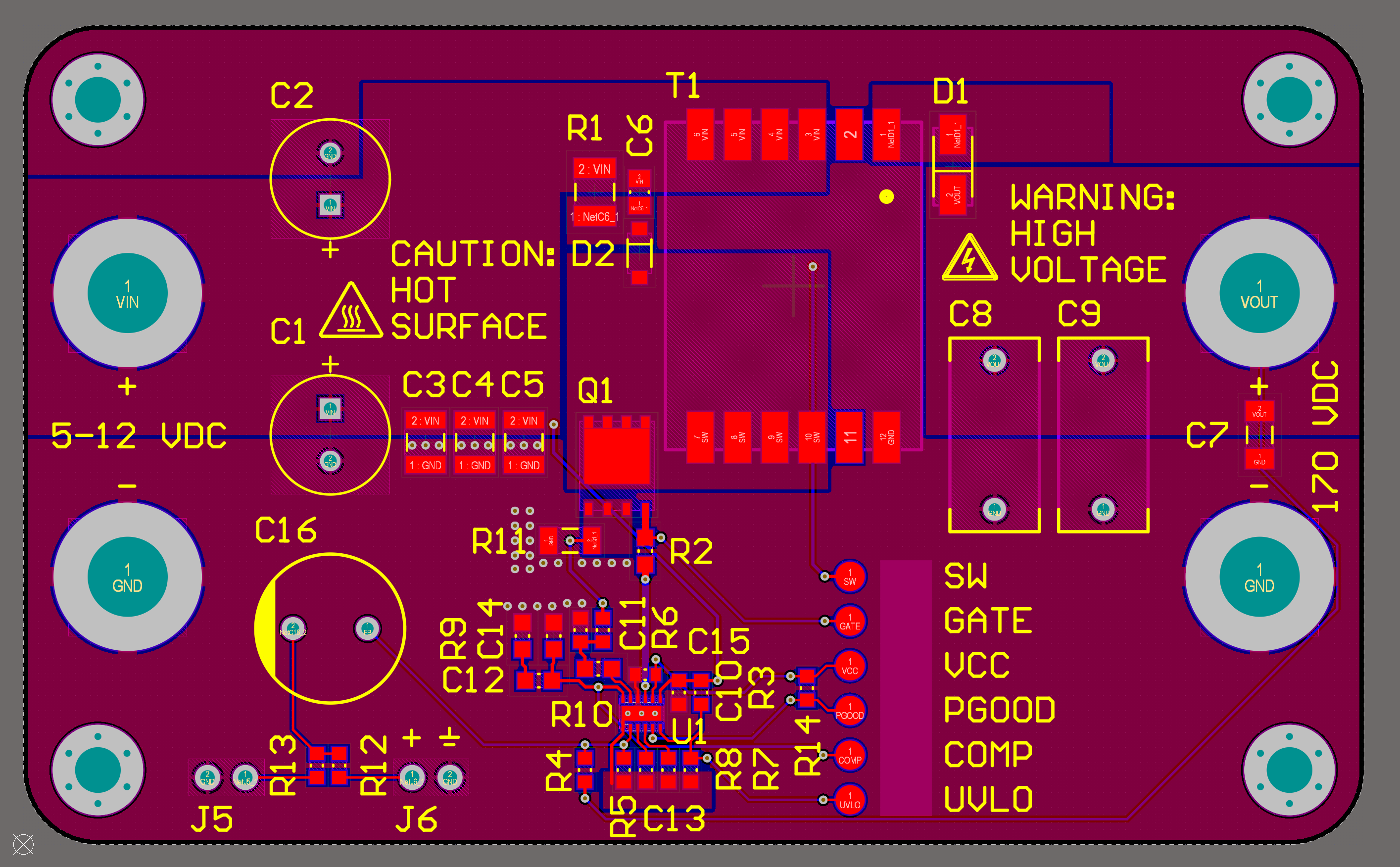
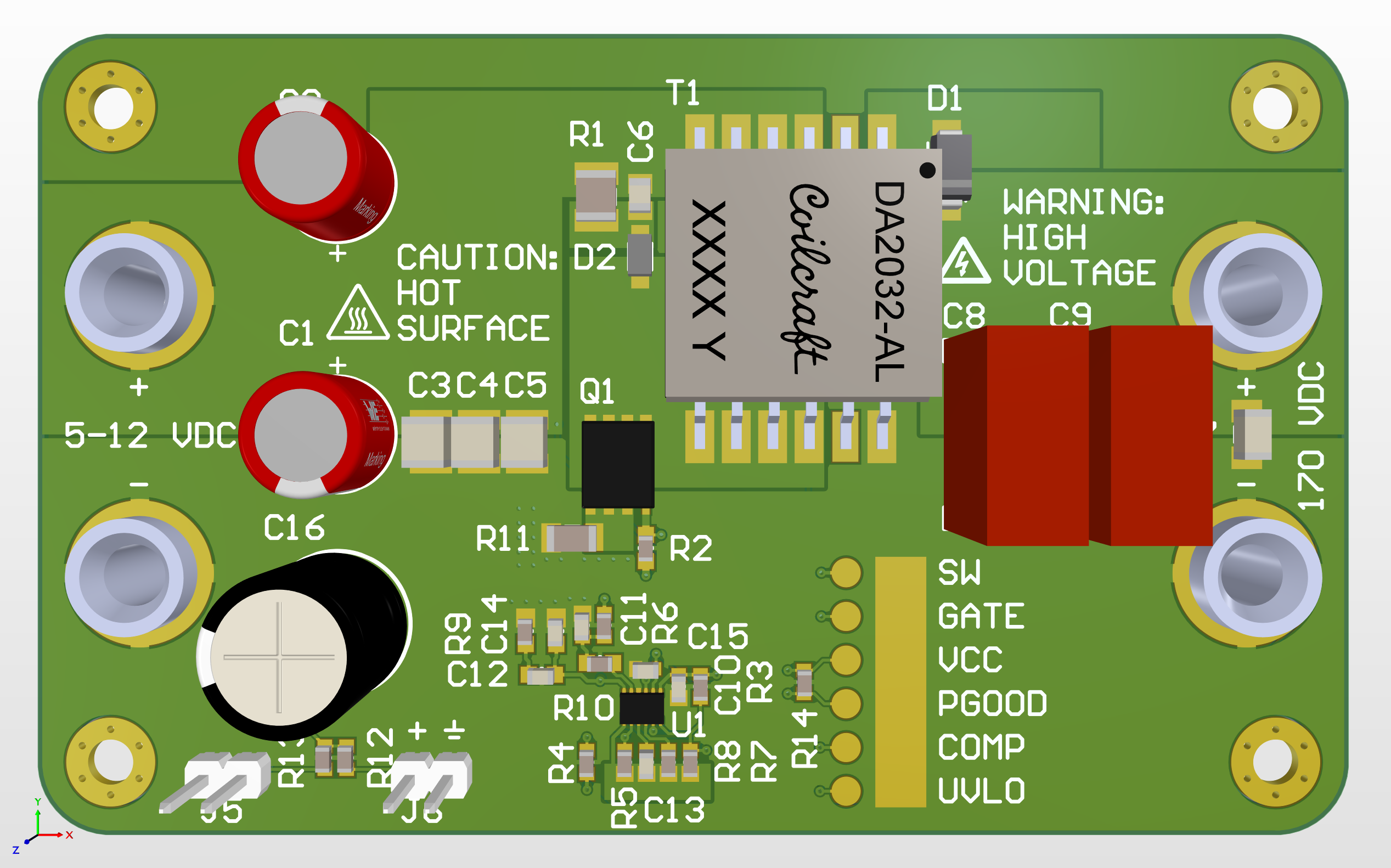
Prototype layout
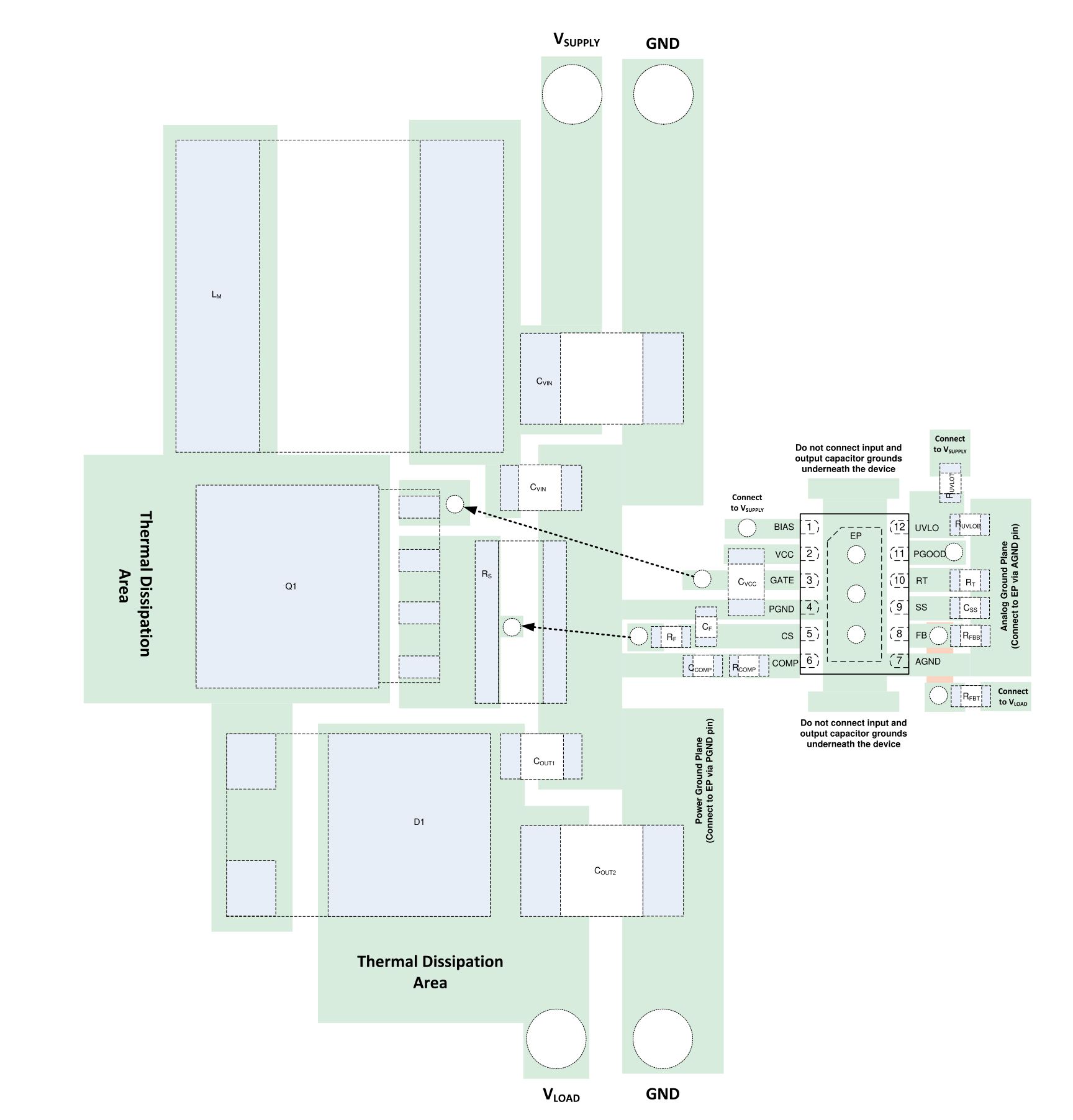
04/18/2020 at 23:29 • 0 commentsFor this project, I wanted to justify all component values from first principles. On the other hand, for PCB layout of a SMPS, I'm more than happy to copy a layout that works. In this regard, the datasheet for the LM5155 provides very helpful layout guidelines and examples, and the engineering team at TI also produced three evaluation boards (in boost, isolated flyback, and SEPIC topologies) that also demonstrate good layout.
---------- more ----------![]()
![]()
For my test board, I wanted to follow in the "evaluation board style", which to me means:
- Medium- to low-density design where there's plenty of room to probe and rework parts. Anything that I think I might tune, I use low-density footprints and leave space to rework the area and bodge on parts.
- Prefer larger component packages that are easier to rework, no smaller than 0603 for passives.
- Lots of test points. Commercial boards often use soldered-on loops for test points, but these get expensive in quantity, and an exposed pad with a nearby ground point works just as well.
- Power terminals accept big banana plugs for fast, positive connections to meters and power supplies.
- Screw holes and standoffs at the corners make it easy to keep the board stationary while attaching probes.
As the flyback power stage is the only thing on the board, routing should be uncomplicated, and I used a 2-layer layout like the examples and commerical evaluation boards.
![]()
![]() Next step: send for manufacturing, assemble & test!
Next step: send for manufacturing, assemble & test! -
First evaluations
04/19/2020 at 19:47 • 0 commentsThe boards were produced by JLCPCB and in my hands within a week, very nice considering concerns about the global economy at the moment. I assembled identical boards, one as a reference and the other to be poked and probed, and sacrificed if needed.
![]() ---------- more ----------
---------- more ----------Load board
I don't have an electronic load, which makes testing power supplies a lot easier. Even if I did, most general purpose e-loads aren't set up well for the corner case of high-voltage, low-current power. Even though this board sources less than 10 W, I'd need an overspecced e-load just to handle the voltage rating, or use something like an SMU (even more expensive).
So along with this board, I also had a second board made that lets me adjust the load manually in steps. Each switch on this board adds a branch with two 1 W 68 kΩ resistors in parallel, or 34 kΩ. 170 V into 34 kΩ gives 5 mA per switch, so the output current can be stepped from 0 - 50 mA.
![]()
Startup transient
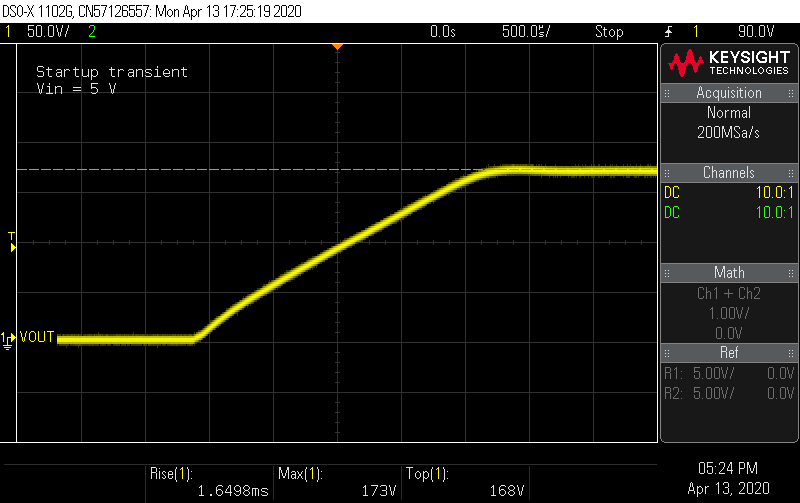
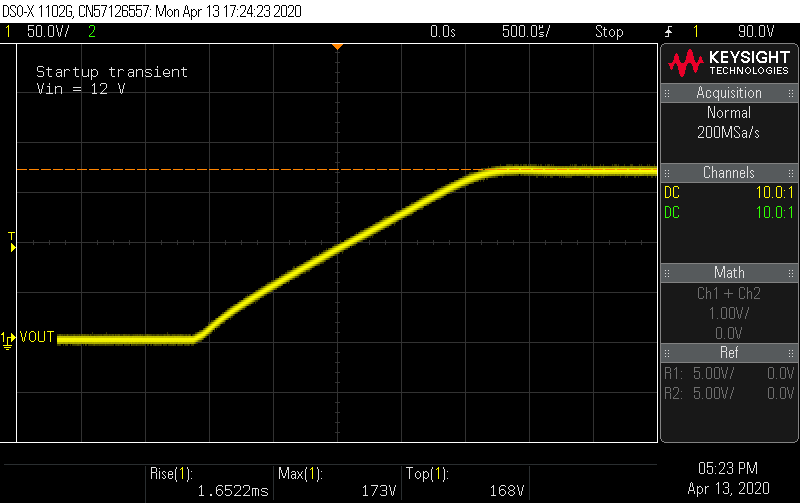
Does it work? Connecting the inputs to a bench supply the and output to a multimeter, I anxiously flipped the switch, and heard ... the satisfying click of my multimeter's autoranging relay followed by a reading of 169 V! Connecting the load board, I flipped the switches and watched the voltage remain rock-steady as I pushed the load current to 50 mA. Satisfied that nothing was going to give off smoke, I started characterizing the board on an oscilloscope.
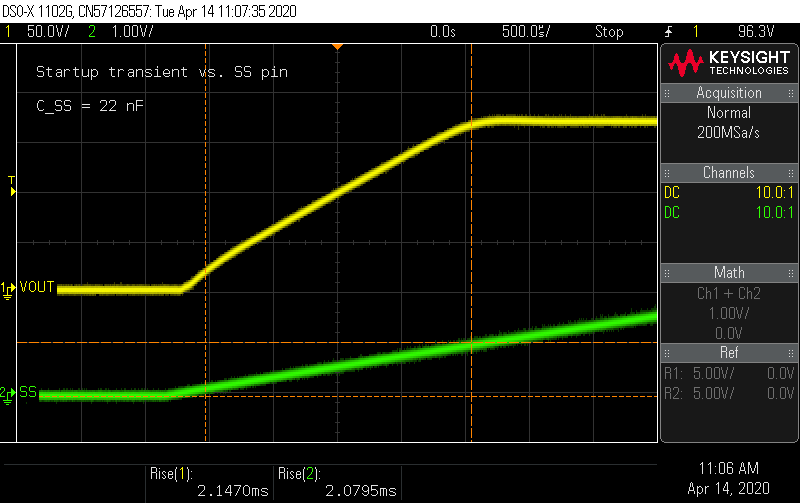
Setting a long time base, I examined the startup ramp transient. At 5 V and 12 V input voltage, it looked identical.
![]()
![]()
The startup time seems fixed. Well, there was that soft-start feature... The soft-start ramps up the feedback control voltage as the soft-start capacitor charges to 1 V. How does the SS pin voltage and ramp time compare to the output voltage? I set the rise time measurement on the output voltage to measure 0 to 100% (usually rise time is cited as 10 - 90%) and an absolute rise time for the other channel with a limit of 1 V.
![]()
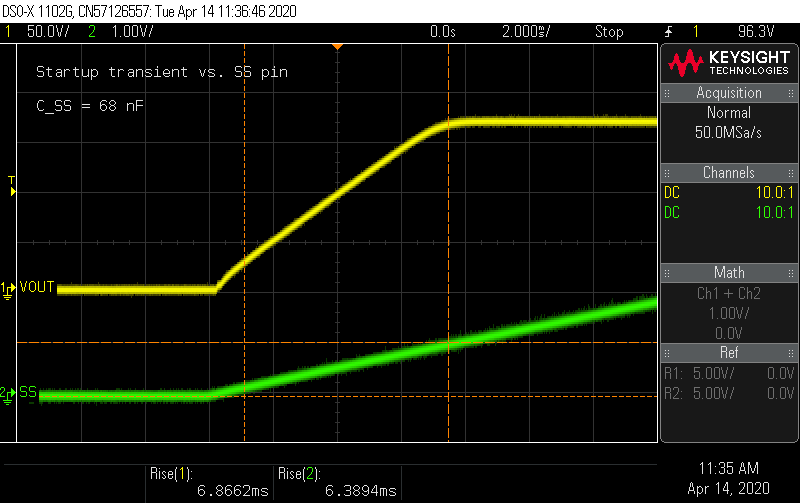
10 µA into 22 nF rises to 1 V in 2.2 ms, so that looks right. What happens if I replace C_SS with something larger, like an extra 68 nF from the compensator circuit? I'd expect the rise time to go to 6.8 ms...
![]()
Bingo! I kind of like this a bit more. The slower rise time appears to eliminate the mild voltage overshoot that's noticeable with the original 22 nF choice.
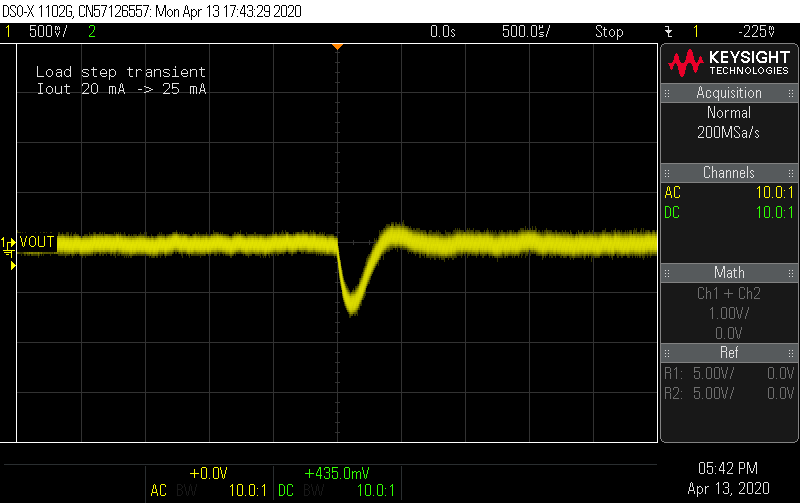
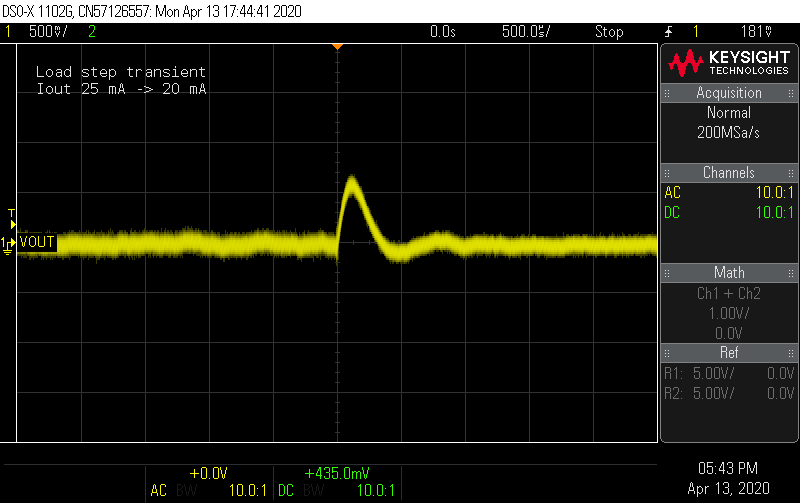
Load transient
Next, how well does the controller handle a sudden change in load? In the simulation, I used a 15 mA load step, but try as I could, there's no way to flip 3 switches at exactly the same instant, so I only captured the step load transient for a 5 mA step. These are AC-coupled captures, so going to zero means a return to regulation.
![]()
![]()
In the design phase, I used a crude estimate of the converter's output impedance to size the output capacitance to limit the load transient to 1 V at a 15 mA load step. In simulation, the result looked closer to 2 - 3 V. Here the transient is about 700 mV for a third the size of the load step, so that the simulation looks like it's predicting things well.
Another way to understand the load transient is look at the feedback loop response. I added a circuit to permit injecting a function generator signal into the feedback loop. Unfortunately, it didn't work as planned. Once the jumper to ground is closed, the large capacitor (1000 µF) pulls down the FB line voltage causing the output voltage to spike. This stresses all the components and destroyed one of the test boards very quickly. The board can't withstand the high voltage during the charging time, even if the coupling capacitor is reduced to 100 µF. It's disappointing this part doesn't work after all the theoretical work that went into designing the compensation network. There are other ways to make measurements of the loop gain, but they involve breaking the feedback loop and will require a board respin. Wary of destroying my remaining board by a careless short of one of those headers, I removed those components for my remaining tests.
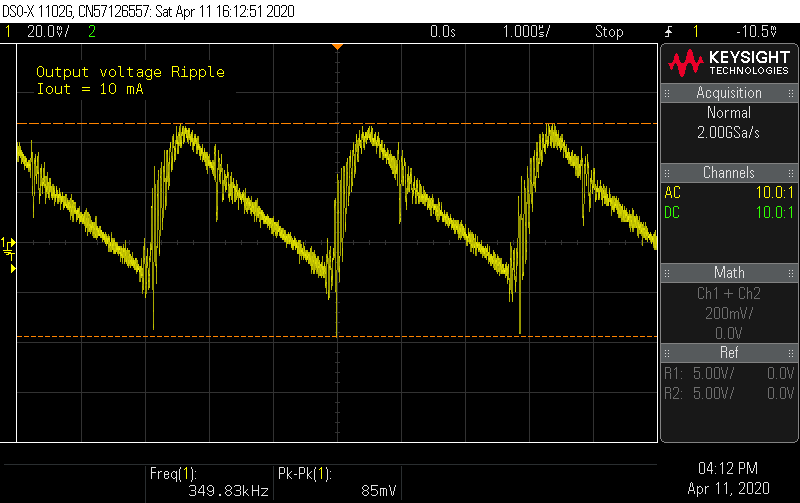
Output ripple
Output ripple measurements were made by probing directly across C7 in AC coupling mode. There's definitely some high frequency component that's modulated with the lower frequency ramp up and down.
![]()
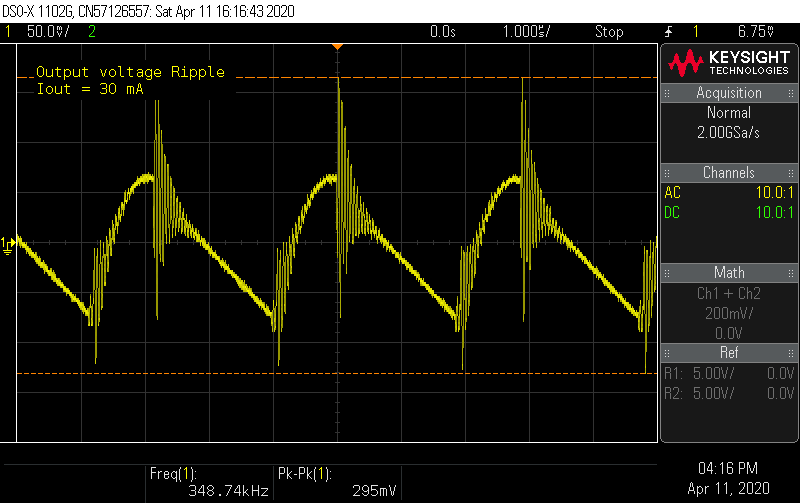
At 30 mA load, these spikes get larger, but overall the ripple is manageable at less than 300 mA. From the output ripple formula, at 30 mA, the output ripple should be about 150 mV, which if you ignore the ringing not predicted by the formula, looks about right on.
![]()
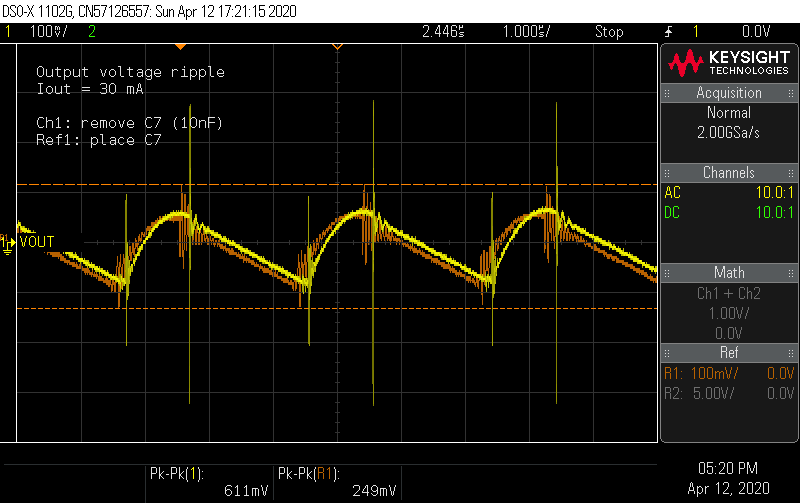
Is the 10 nF capacitor C7 doing anything? Should it get to keep its job? Let's remove it and see what happens.
![]()
Seems the 10 nF ceramic capacitor really does help after all.
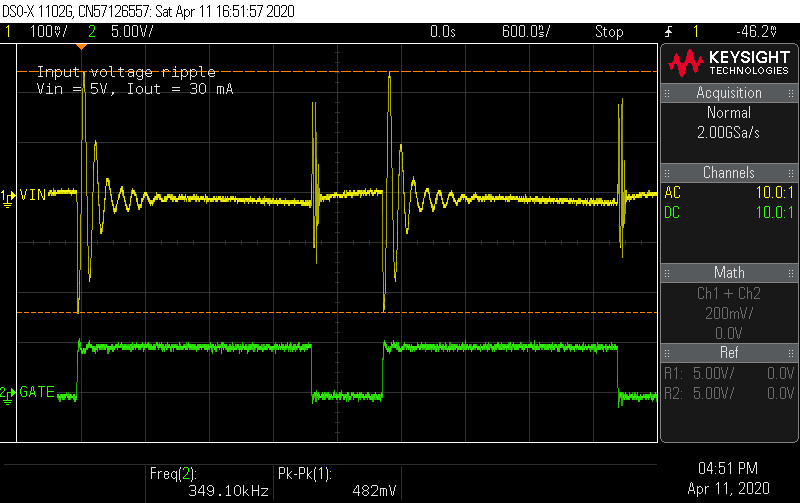
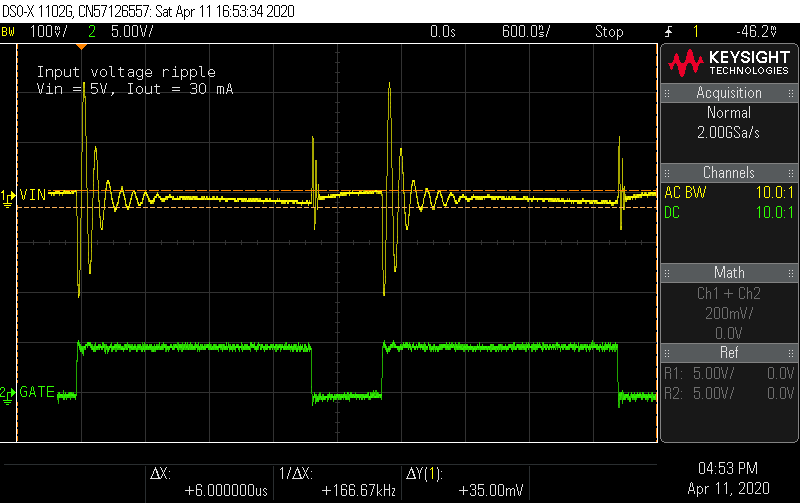
Input ripple
Probing directly across the input terminals, I measured the input ripple. There are ringing waveforms at the edges of the switching cycle, but the low frequency ramp appears to have a peak-to-peak amplitude of about 35 mV, which was close to the design target.
![]()
![]()
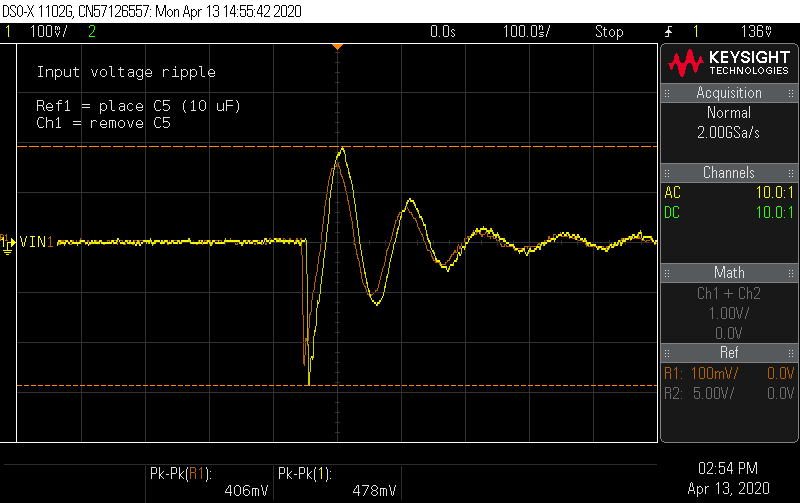
What effect do the three ceramic caps C3, C4, and C5 have? Removing the last one shows some mild effect.
![]()
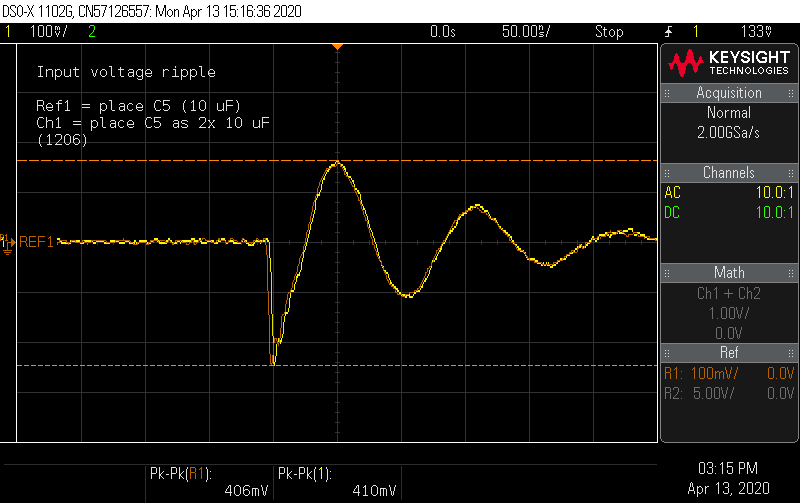
I squeezed two 1206 10 µF caps into the space of one 1210 and measured the result. It appears the point of diminishing returns has been reached.
![]()
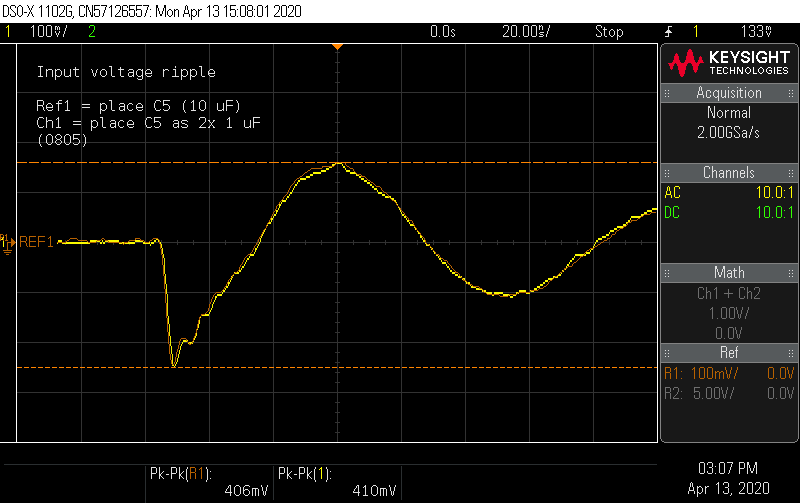
What about additional capacitance in a lower decade? I tried the same trick with some 1 µF 0805 caps.
![]()
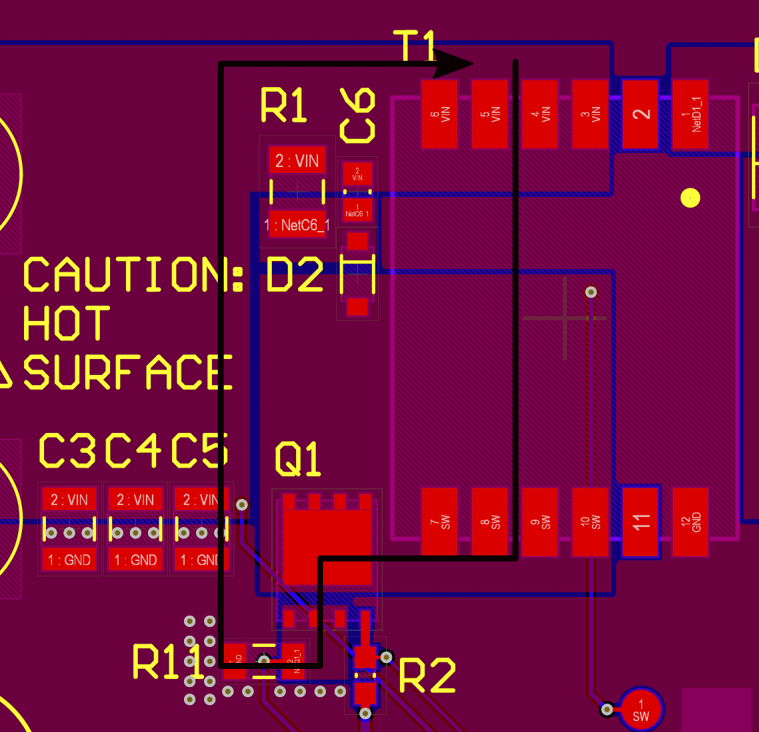
Unfortunately, it appears additional capacitance cannot reduce the spikes at the input. The more I looked at things, the more I suspect that a poor layout choice might be responsible. When the switch turns on, the source current instantly jumps to the average inductor current. Small capacitors will be the lowest impedance path for a sharp current step, so the current will prefer to go through the bank of ceramic capacitors. Under load, the inductor current is substantial and any stray inductance in this loop will cause sharp voltage spikes. Inductance is related to loop size, and the placement of the capacitors forces a sizeable loop on the top layer. Current can also flow on the bottom layer under the path from T1-Q1-R11, around the trace that cuts the ground plane, and then double back to reach C3-C5. It's hard to guess what is the actual lower inductance path.
![]()
A better layout would be to move C3, C4, and C5 directly adjacent to the transformer pads and let the current flow underneath the path on the bottom layer, which greatly reduces the loop size. This too will require a board respin.
![]()
-
More evaluations
04/19/2020 at 22:20 • 0 commentsThe previous update looked at voltage ripple and transients. Another important area to investigate is the switching waveforms. This shows the switch node and gate voltages.
![]() ---------- more ----------
---------- more ----------And a close up:
![]()
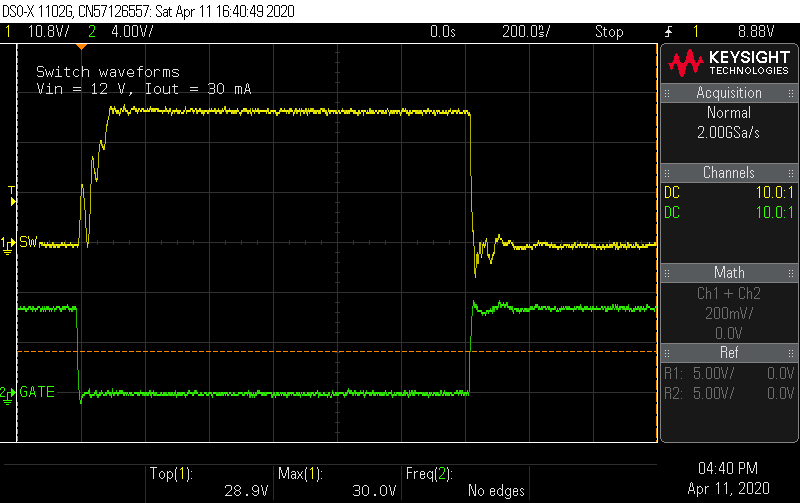
The first thing to notice is that the ringing predicted by the simulation is almost nowhere as bad. Instead of rising and overshooting the off-state voltage of 22 V, it's taking a while to reach that level while ringing on the way up. This happens regardless of input voltage:
![]()
![]()
What's going on here? The snubber was expected to clamp the switch node voltage to 32 V, but the voltage never gets close. Before investigating further, it's worth commenting on the gate waveform. I added a 0 Ω series jumper in the design as an option to damp any ringing at the gate. The BSC059N04LS6 datasheets puts the Vgs(th) figure at 2.3 V max, so even at 5 V input, the switch is squarely on, and it seems the waveform is clean enough not to require additional series resistance at the gate.
Back to the weird rising waveform at the switch node. Probing the secondary side reveals a clue.
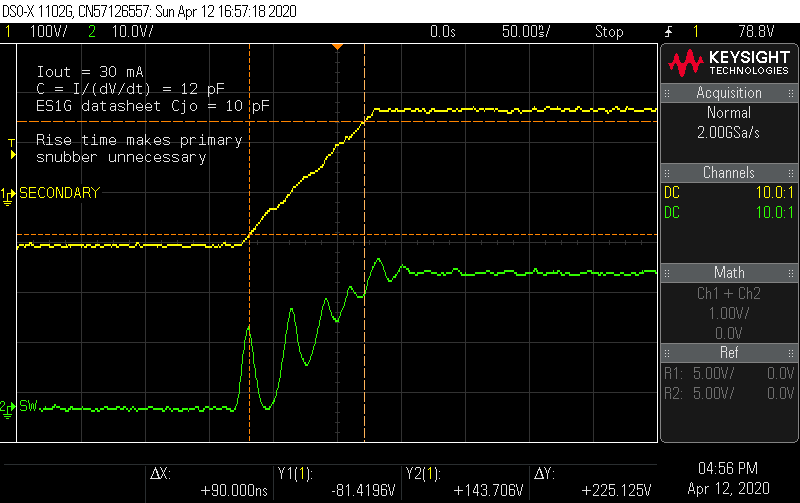
![]()
The secondary voltage ramps as if a current source is charging a capacitor, which happens to be the real junction capacitance of the diode, closely matching the datasheet value. The ringing at the switch node has to follow this voltage ramp, so the ringing starts from a lower amplitude and decays before the switch node voltage reaches the full off-state value. Here is the first big departure from the simulation: it appears the diode model for the ES1G doesn't accurately model the junction capacitance. When I re-ran the simulation, it predicted a diode rise time of less than 25 ns.
As a side-effect, the primary side RCD snubber is not really helping anything. The voltage across the snubber capacitor remains about 16 - 17 V, so I removed it and found no change in power consumption.
The simulation also predicts an oscillation at the secondary when the diode turns off, which is confirmed on the oscilloscope.
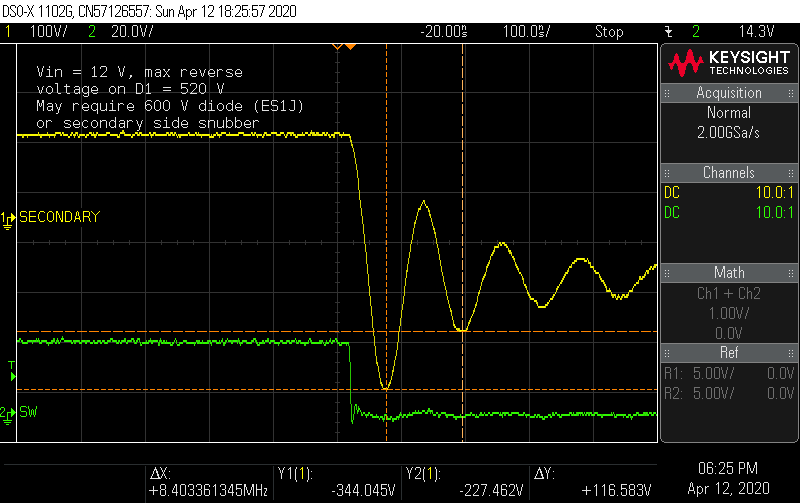
![]()
With the other side of the diode at 170 V, the diode sees reverse bias spikes of nearly 520 V. This ES1G diode has a VRRM (maximum repetitive reverse voltage) of 400 V, so this ringing is probably going to reduce the service life of this diode. There are a few options to correct this situation: place a higher-rated diode (such as the 600 V ES1J), add a snubber across the diode, or try a different diode with better reverse recovery characteristics.
How much will a snubber help, and what will it cost? To experiment with a snubber, I first measured the frequency of the oscillation. The resonance exists between the transformer's leakage inductance as seen on the secondary side, and the parasitic capacitance of the diode junction as it goes through reverse recovery.
![]() The primary side leakage inductance of the DA2032 is 150 nH, so it will n^2 * 150 nH or 15 µH on the secondary side. At an oscillation frequency of 8.4 MHz, the capacitance for this resonance is 24 pF, and the characteristic impedance (sqrt(L/C)) is 792 Ω. An RC snubber design trial should start with this resistance and a capacitance of 4 - 10x the parasitic capacitance.
The primary side leakage inductance of the DA2032 is 150 nH, so it will n^2 * 150 nH or 15 µH on the secondary side. At an oscillation frequency of 8.4 MHz, the capacitance for this resonance is 24 pF, and the characteristic impedance (sqrt(L/C)) is 792 Ω. An RC snubber design trial should start with this resistance and a capacitance of 4 - 10x the parasitic capacitance.I have some assorted 250 V 0603 caps in the 100-1000 pF range, so I bodged on two in series to withstand 500 V. A 0603 820 Ω resistor exploded instantly. A single 1/4 W through-hole resistor also started smoking with a second. Substantial power was being burned off in this snubber. Finally I tried a fixture of four 1/4 W 3.2 kΩ resistors soldered in parallel, and even then, the paint on the resistors began to discolor within a few minutes. This wasn't looking promising, but I took some measurements nonetheless.
![]()
The snubber has reduced the reverse bias spike to under 460 V, but at a dear cost. Measuring the AC voltage across the resistor network showed it was dissipating over 1/2 W. That's going to wreck the efficiency of the converter, and for what? A higher-rated diode is still needed.
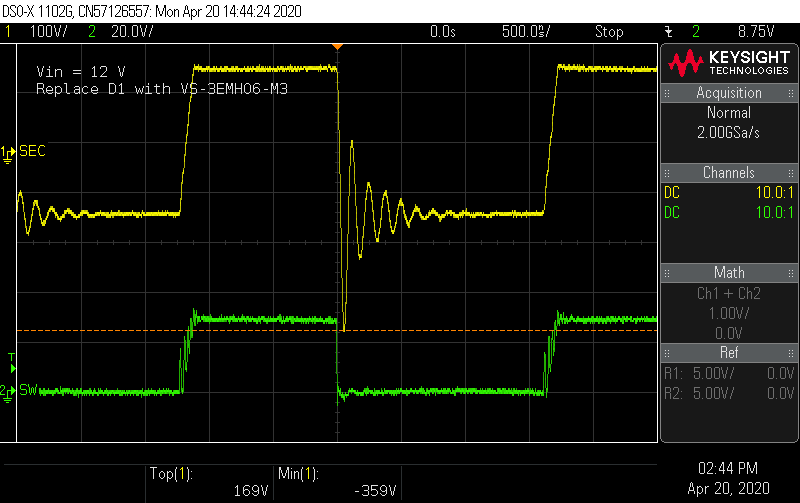
Dissapointed, I removed the bodged-on snubber, and ordered a few pieces of the ES1J and another diode I found, the VS-3EMH06. This diode is a "hyper-fast" rectifier (evidently the ranking is standard, fast, ultra-fast, super-fast, hyper-fast ... real helpful) with also a "soft recovery", so I'm curious to see how it will perform. There are even faster diodes out there in this lineup, but they are rated for higher current, are more expensive, and use a larger footprint. There are not a great many diodes that are designed for modest forward current, high reverse voltage, and highest speed. I'll see how this diode performs in the next update.
-
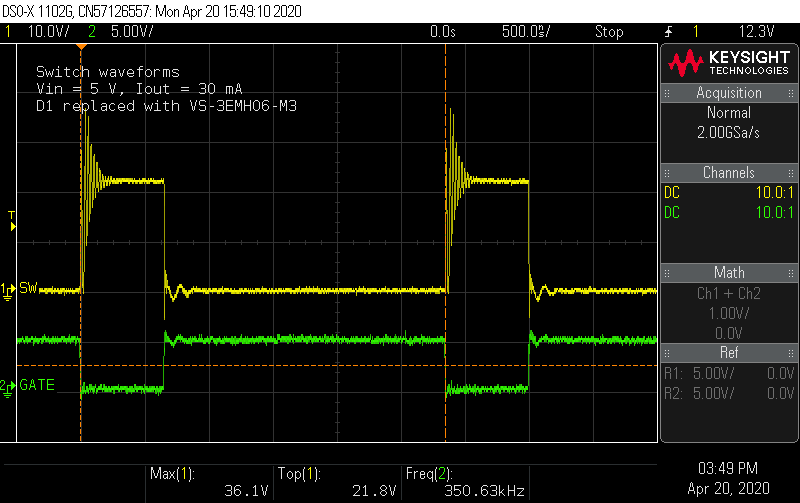
Parts swapping and efficiency measurements
04/21/2020 at 05:19 • 0 commentsI got a shipment with the 600 V-rated ES1J and the VS-3EMH06-M3 diodes. How does a "hyperfast" rectifier compare to the "ultrafast" part I started with? Looking at the voltage on the rise time on the secondary shows it's close to twice as fast (47 ns vs. 90 ns). Already it appears the switch node ringing is starting at a higher amplitude.
![]() Probing the switch node shows a ringing waveform that looks much closer to the simulation. At the maximum inductor current condition, the voltage spikes are still 10% below the MOSFET Vds limit, without any snubber.
Probing the switch node shows a ringing waveform that looks much closer to the simulation. At the maximum inductor current condition, the voltage spikes are still 10% below the MOSFET Vds limit, without any snubber.![]()
Lastly, the reverse recovery situation looks about the same, with the reverse voltage spiking to 530 V.
![]()
Overall, it seems this new diode is nothing special by comparison, but the 600 V rating is important given the voltage ringing during reverse recovery.
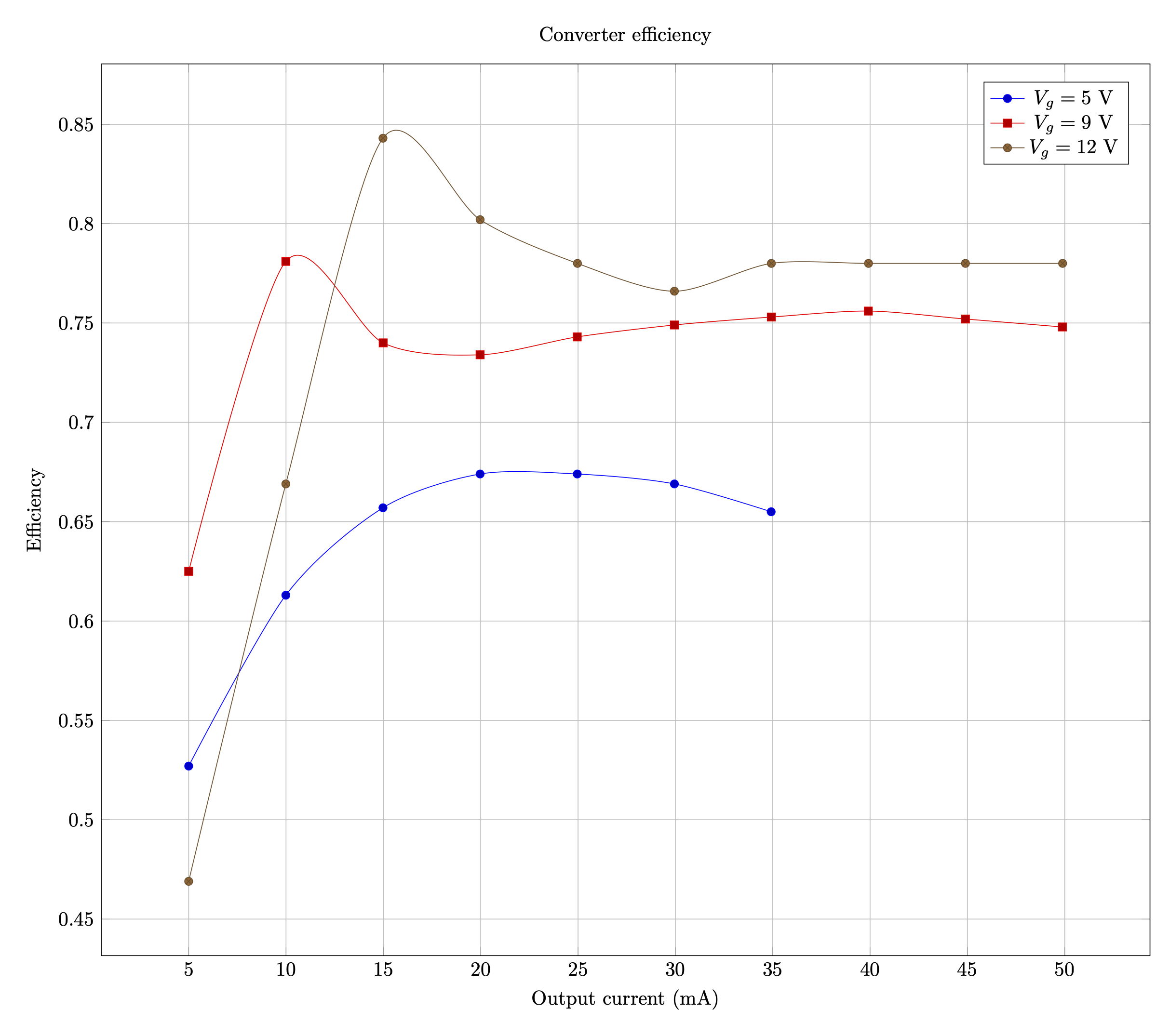
Efficiency measurements
I waited to make efficiency measurements because I wanted to settle on a configuration to use after considering options for the snubbers or other adjustments. For this test, the measurements were taken with the VS-3EMH06-M3, and without RCD snubber network. I used the source display on my bench power supply to read the input power, and measured the voltage at the converter's output terminals and the current between the converter and load board. Of course, it'd be nice to do all this with ATE that would gather the data while I made on some coffee, instead of by hand ... perhaps someday.
![]()
![]()
At 9 and 12 V, the converter is about 75-80% efficient, with a sweet spot around 15-20 mA where it peaks over 80% with 12 V input. It would have nice to be consistently above 80%, but it appears core losses in the transformer are the limiting factor. It is easily the warmest component on the board during operation.
I didn't take measurements at 5 V beyond 35 mA, because at high load, the current in the transformer is high enough that causes a thermal runaway. Heat increases resistance and voltage drop, so the converter adjusts by increasing duty cycle and average current, which further increases heat. Eventually the converter hits the current limit or the transformer core begins to saturate. At the 5 V, the converter should be thermally derated to 25 mA maximum current to keep the transformer from overheating, unless active cooling is done.
The last parts experiment I had was to test polypropylene (PP) output capacitors. PP is supposed to have lower dissipation factor by an order of magnitude compared to polyethylene terephthalate (PET), so it should handle pulse currents better. Would it help improve efficiency beyond the 75-80% level? I replaced the output caps and reran the efficiency experiment. The result was basically a wash. A few fraction of percentage points here, a few there. No data point changed by more than 1 %, which doesn't justify their added cost.
-
Prepping for rev B
04/24/2020 at 17:31 • 0 commentsWhat worked out well with the initial build:
- Converter maintained voltage regulation well beyond the 30 mA output design limit
- Output ripple was well-controlled
- RCD snubber proved to be unnecessary to protect the MOSFET
- Load transient response demonstrated good loop stability
What was a disappointment:
- The no-break injection circuit didn't work at all and destroyed both the MOSFET and diode on one prototype
- Input voltage ripple shows large spikes
- Efficiency remains close to, but below, 80% under full load
- Thermal problems at high load and low input voltage
Since everyone is still going nowhere, I sent off a second board revision for manufacturing with a couple of changes:
- I removed the no-break injection circuit and replaced it with the more "traditional" way of doing voltage injection by breaking the loop across a small series resistance. This method is documented in TI's AN-1889 and requires a wideband injection transformer. These are a bit of a back-catalog item of test equipment, but it turns out they are eminently homebrew-able with excellent results.
- The ceramic input capacitors have been moved next to the transformer, with a solid ground plane underneath. Additionally, I added a couple of footprints for some 1 µF or smaller capacitors. Throwing additional capacitance in has diminishing returns, but it's easy to leave them unpopulated if they also prove to be of no help. This change also means I can trim 5.5 cm^2 of board space without increasing component density.
The efficiency of the converter could be improved by using a lower switching frequency to reduce switching losses. The choice of switching frequency was driven by the limit I chose on inductor current ripple. Lowering the switching frequency will increase the current ripple and increase the minimum load where the converter begins to operate in DCM. It will also precipitate re-evaluating most of the passive component values, so I'll leave this be for the moment.
Nixie Tube 170 V flyback DC-DC power converter
Design walkthrough and evaluation of a flyback converter from scratch
 James Wilson
James Wilson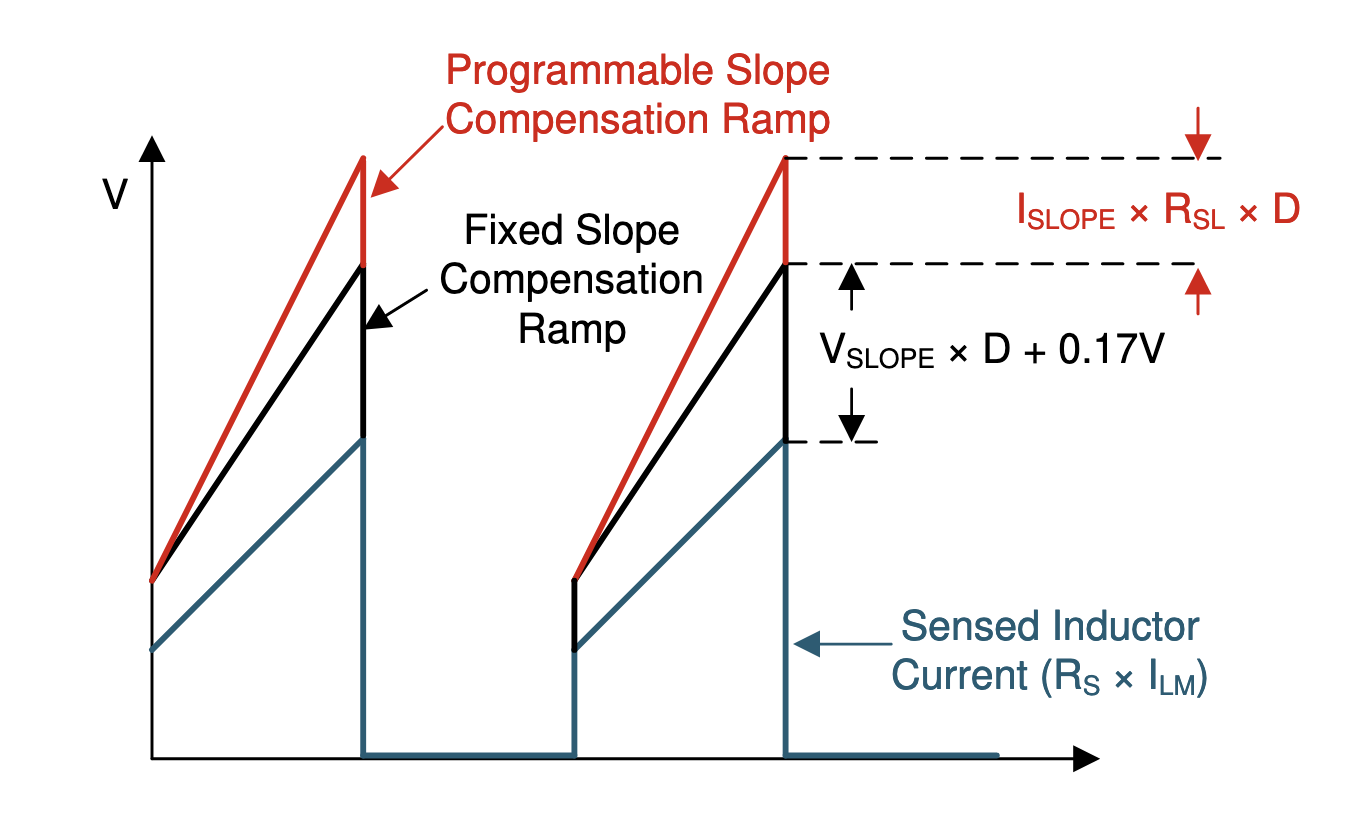

 I changed the initial load to 11.33k to get a 15 mA output current and added time-delayed step current sources IG1 and IG2 to simulate a load step-up and step-down of 15 mA. Here's the output voltage plot, showing the startup ramp and load step at 5 ms/6 ms:
I changed the initial load to 11.33k to get a 15 mA output current and added time-delayed step current sources IG1 and IG2 to simulate a load step-up and step-down of 15 mA. Here's the output voltage plot, showing the startup ramp and load step at 5 ms/6 ms: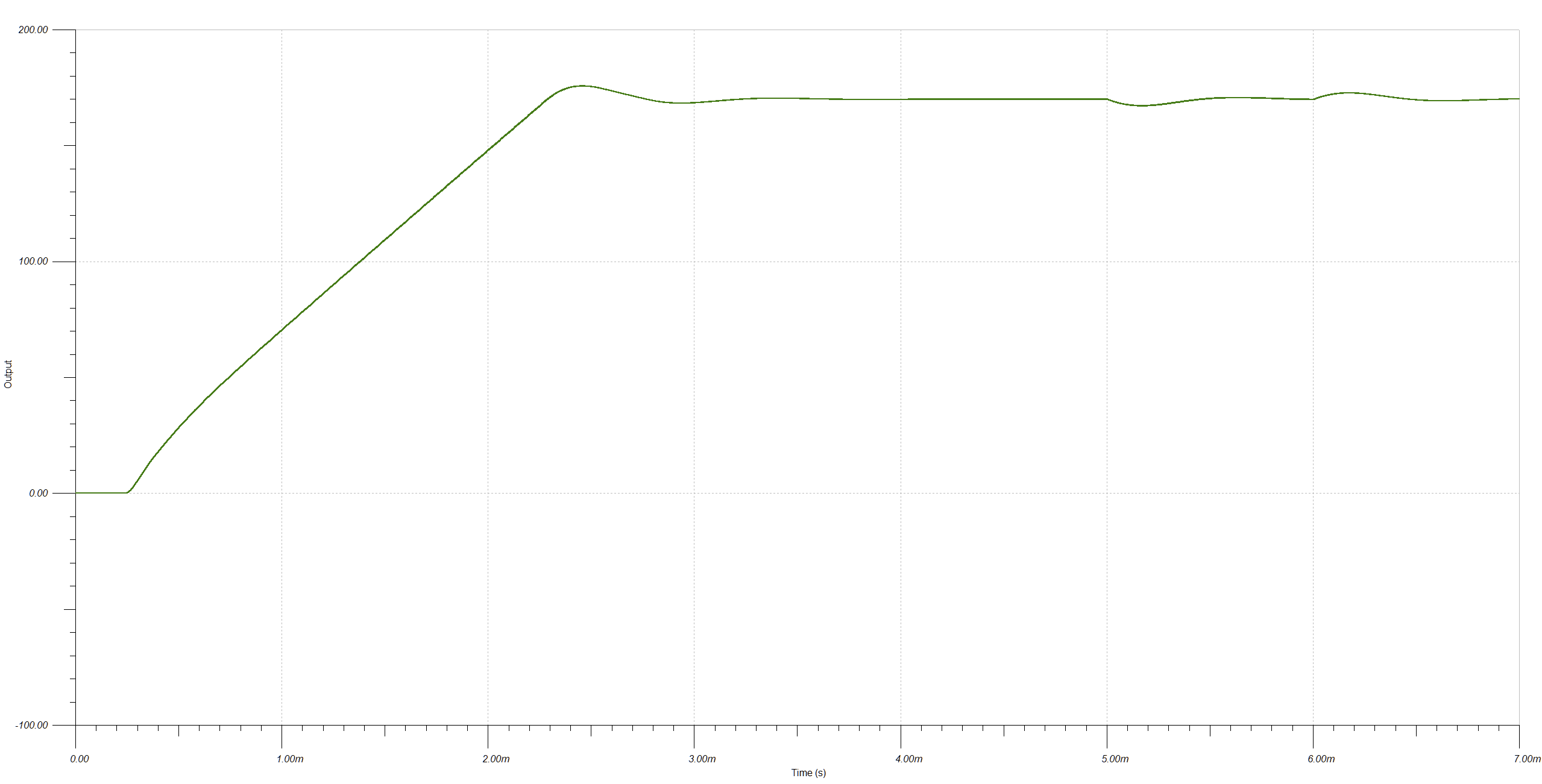 Close-up of the load step transient shows the transient is larger than 1 V as predicted by formula used to pick the output capacitance, but it seems acceptable for the application. The converter returns to regulation within a millisecond and shows good stability.
Close-up of the load step transient shows the transient is larger than 1 V as predicted by formula used to pick the output capacitance, but it seems acceptable for the application. The converter returns to regulation within a millisecond and shows good stability.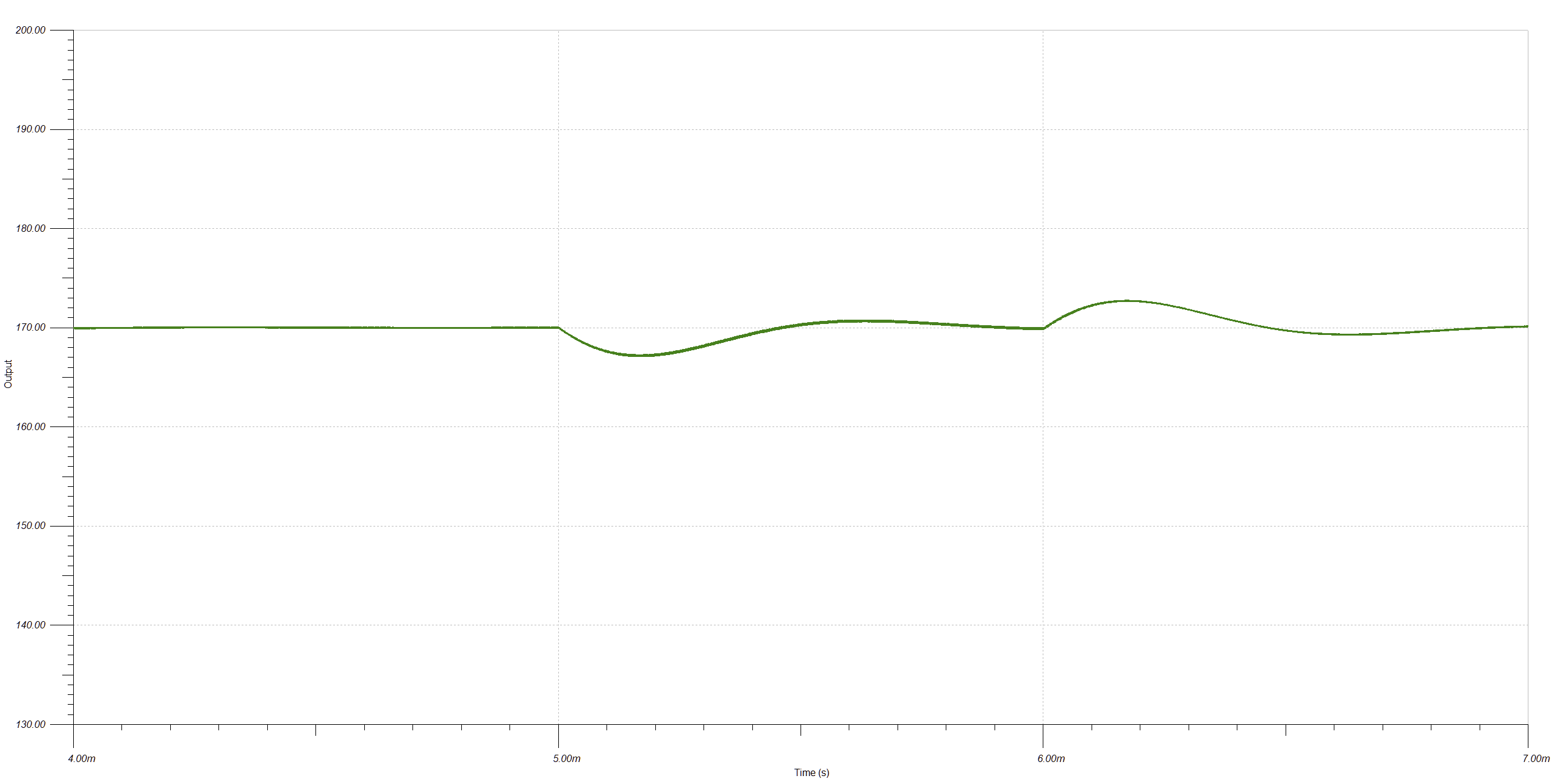 Looking at the switch node or MOSFET drain at full load, there's a problem: the voltage is spiking above 40 V and will need a snubber.
Looking at the switch node or MOSFET drain at full load, there's a problem: the voltage is spiking above 40 V and will need a snubber.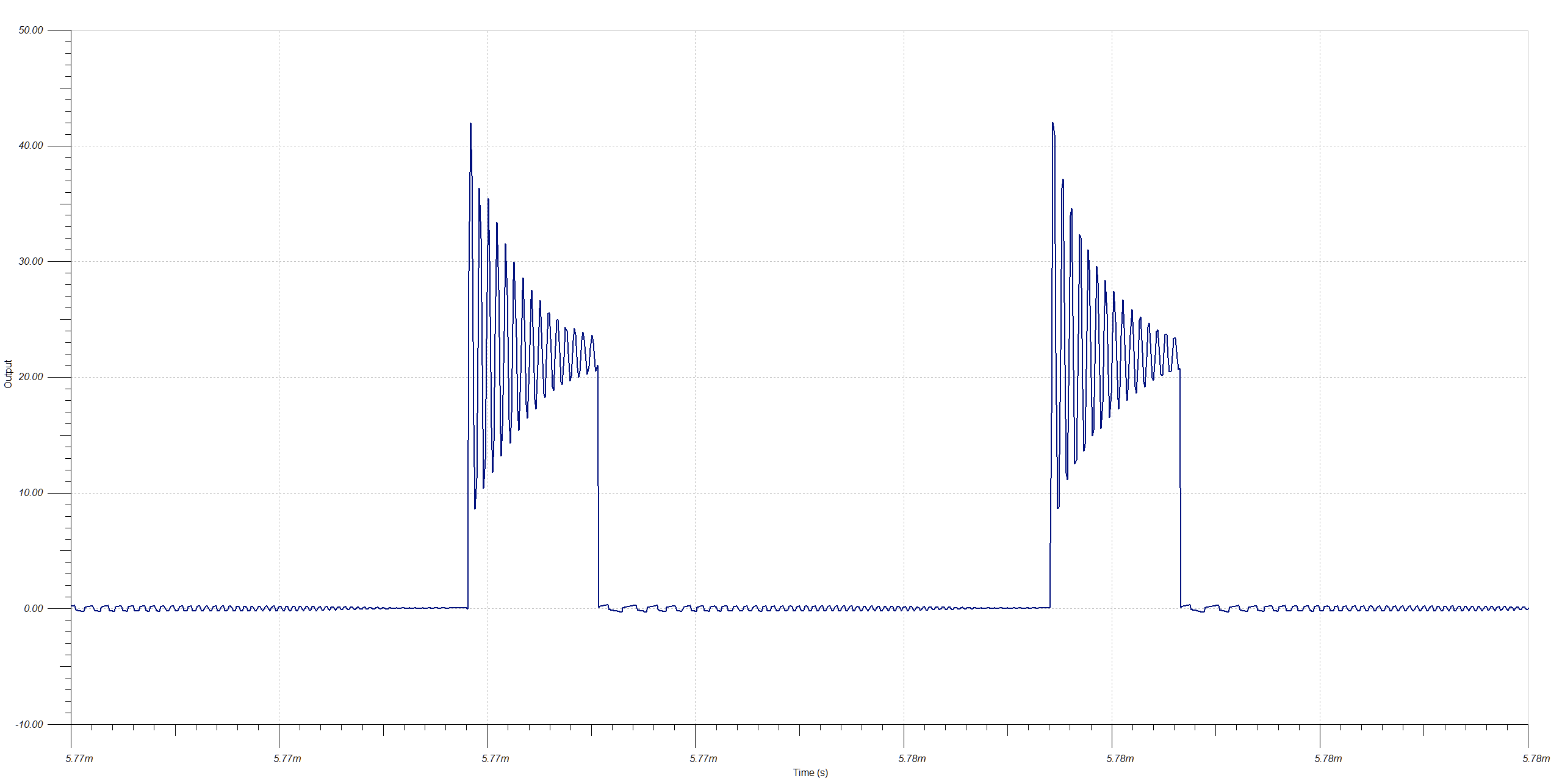
 The simulation with this circuit added shows the switch node voltage gets clamped at 32 V as predicted. There's still a lot of ringing, but the goal of protecting the MOSFET has been achieved. Snubbers always need experimental verification and tuning, but this looks like a promising starting point.
The simulation with this circuit added shows the switch node voltage gets clamped at 32 V as predicted. There's still a lot of ringing, but the goal of protecting the MOSFET has been achieved. Snubbers always need experimental verification and tuning, but this looks like a promising starting point.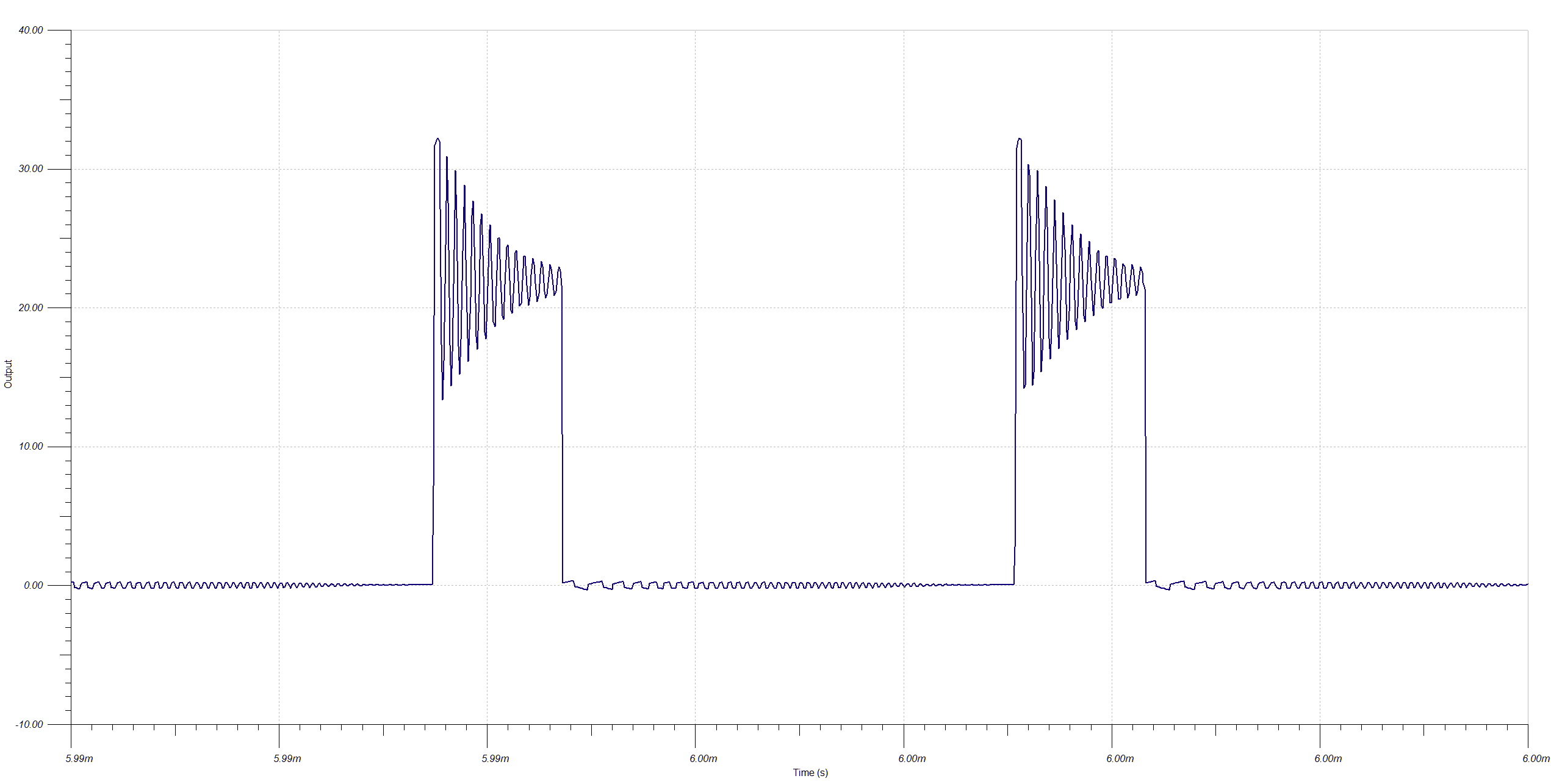

 Next step: send for manufacturing, assemble & test!
Next step: send for manufacturing, assemble & test! ---------- more ----------
---------- more ----------





 The primary side leakage inductance of the DA2032 is 150 nH, so it will n^2 * 150 nH or 15 µH on the secondary side. At an oscillation frequency of 8.4 MHz, the capacitance for this resonance is 24 pF, and the characteristic impedance (sqrt(L/C)) is 792 Ω. An RC snubber design trial should start with this resistance and a capacitance of 4 - 10x the parasitic capacitance.
The primary side leakage inductance of the DA2032 is 150 nH, so it will n^2 * 150 nH or 15 µH on the secondary side. At an oscillation frequency of 8.4 MHz, the capacitance for this resonance is 24 pF, and the characteristic impedance (sqrt(L/C)) is 792 Ω. An RC snubber design trial should start with this resistance and a capacitance of 4 - 10x the parasitic capacitance.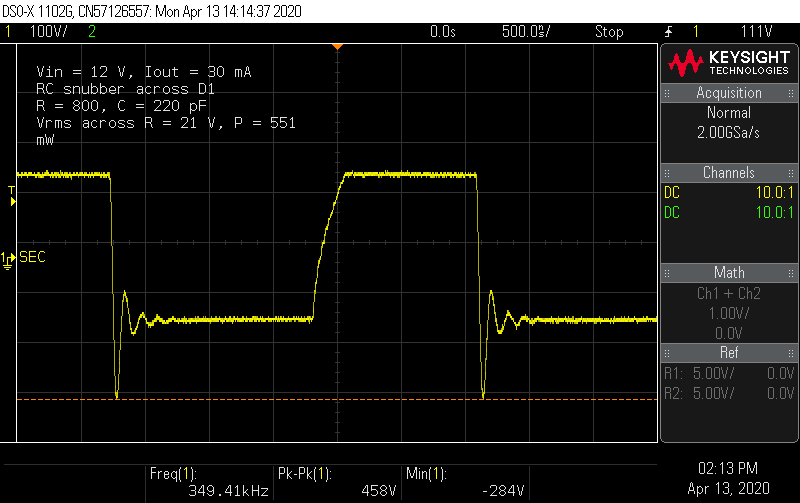
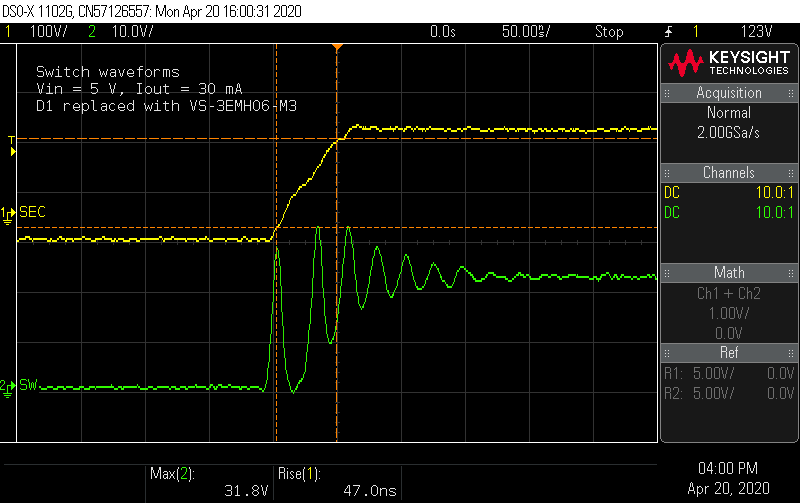 Probing the switch node shows a ringing waveform that looks much closer to the simulation. At the maximum inductor current condition, the voltage spikes are still 10% below the MOSFET Vds limit, without any snubber.
Probing the switch node shows a ringing waveform that looks much closer to the simulation. At the maximum inductor current condition, the voltage spikes are still 10% below the MOSFET Vds limit, without any snubber.