I don't know why I heard about the radix sort algorithm only recently. I have seen it mentioned, among many other algorithms, but I had not looked at it, leaving this subject to the sorting nerds. Until I watched this :
This is very smart and useful but I'm not building a sorting algorithm now. However I can reuse some of these tricks to build, or compile, a semi-dynamic data structure (write-only once) that is both compact and efficient.
Let's go back to my first version of the netlist probe:
Each signal driver must manage a list of its sinks and I first implemented it as a linked list, borrowing some words of memory from each sink structure. Memory-wise, the memory overhead is minimal because one sink can be linked to only one source. The "pointer" of the linked list is both the desired value and the pointer to the next sink (unless it's the last). It avoids any malloc() and meshes directly in the existing structures, however in return they become more complex and harder to mange. The insertion and scan algorithms are a bit cumbersome...
The new version allocates a single chunk of memory to store simple lists of sink addresses (called sinks_list).
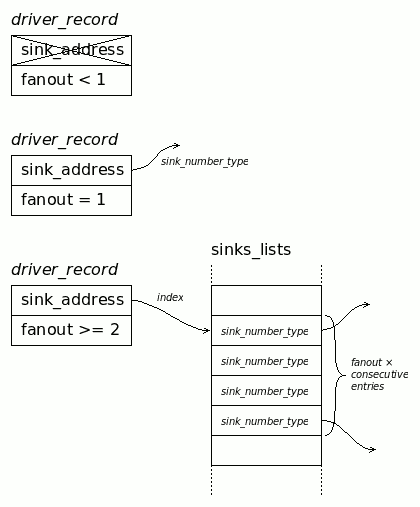
This allows the sink descriptors to be a single number, which is the address of the source/driver. It's easy to manage. As shown in log 3. Rewrite, the driver only contains a fanout number and an address:
- If the fanout is 1, the address is a direct sink address.
- If the fanout is 2 or more, the address is an index in the unified array of addresses, pointing to fanout× contiguous sink addresses.
Building an appropriate compact structure in one pass is not impossible but would require many inefficient re-allocations. However, with 3 passes, it's easy !
- After the first netlist scan, all the drivers have their fanout count updated.
- A second pass creates a counting variable, then for each driver with more than 1 sink, the fanout is added to the counter, which is then put in the address. It's called the "prefix sum"
- The large memory chunk can be allocated because we know exactly how many items it will contain, and the intermediary values of the counter point just beyond the end of each sub-list. The third pass re-scans all the sinks, check the driver, then (if fanout > 1) get the index, decrement it and finally store the sink address to the main list array. As explained in the video, everything falls into place neatly because pre-decrementing ensures that the last write it to the first element of the list.
With this method, there are more simpler loops but each lookup is faster, creating fewer cache faults for example.
This wouldn't have been considered possible if I had never watched the video above, and I think I'll apply this method in more places :-)
 Yann Guidon / YGDES
Yann Guidon / YGDES
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.