VMC Tuning
The last log walked through some issues seen with implementing virtual model control on the legs. I spent some more time debugging the issues. The first thing I did was to continue tuning the system. There are a lot of parameters in this system. These are the PID current controller parameters, the VMC effective stiffness and damping, and gain parameters which describe the motor and the mapping from torque to current. I spent time tuning all of these, and was able to get somewhat better results. One major improvement was shifting the current controller from mostly proportional to mostly integral. This is due in part to the single-sided current sensing we have. The current control therefore is somewhat odd and discontinuous.
} else if(control_type[i] == CURRENT || control_type[i] == PROPRIOCEPTIVE_PRIMITIVE)
{
if(motors[i].current_ma_setpoint >= 0)
{
float cmd = calculate_pid(&cur_params[i], motors[i].current_ma_setpoint, motors[i].current_mA);
// Only allow forward drive
if(cmd > 0)
{
tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 1 : 0, 0);
tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 0 : 1, (int32_t) cmd);
}
else
{
tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 0 : 1, 0);
tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 1 : 0, 0);
}
}
else
{
// Flip direction of control and direction of setpoint
float cmd = calculate_pid(&cur_params[i], -motors[i].current_ma_setpoint, motors[i].current_mA);
// Only allow reverse drive
if(cmd < 0)
{
tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 1 : 0, 0);
tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 0 : 1, 0);
}
else
{
tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 0 : 1, 0);
tcc_set_compare_value(&modules[i], (motors[i].reverse_direction) ? 1 : 0, (int32_t) cmd);
}
}
}If a proportional controller commands driving in the opposite direction of what I know the current should be, I don't command negative. Instead I drop to 0 command. In the next control loop, we then expect the current to shift towards zero, and the controller kicks back on. This inherently means even in a perfect world a proportional controller would bounce around the desired current. However, an integral controller has some inertia to it and would be expected to bounce around less. In testing, this does seem to work. The image below shows the current controlling on one example. The command is oscillatory due to the VMC tuning, but the current tracking looks pretty good.
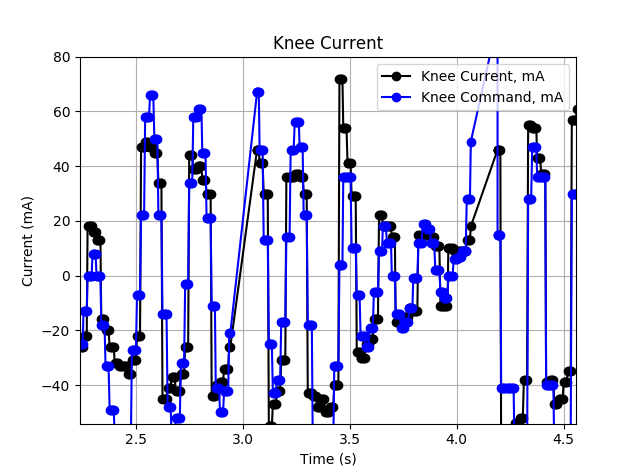
The image below shows the (unloaded) proprioceptive control that I achieved. However, when I tried to have all four legs use this controller to walk, it doesn't work well. The proprioceptive control is just not ready. I therefore dug deeper into the potential issues.
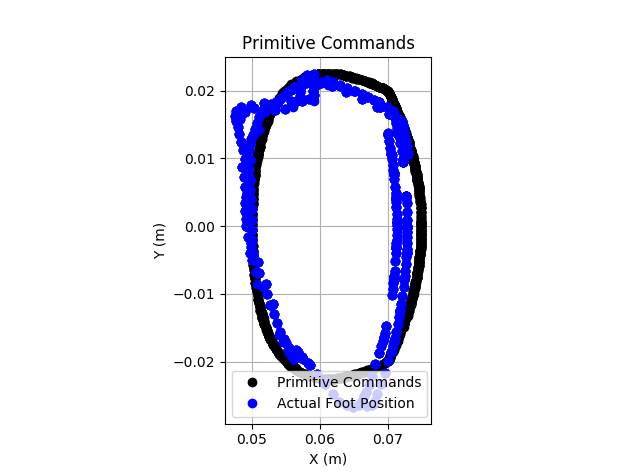
Computational Issues
The motor controllers use a ATSAMD21 Cortex M0+ running at 48MHz. This is a decent microcontroller, but critically it does not have an FPU. Some benchmarks with the same CPU show that floating point multiplication requires ~16.5X the time of integer multiplication, and floating point division is ~14X slower than integer division. Note that the exact timing does depend on the exact data and optimizations, but nonetheless it is clear that floating point math is much slower than integer math. I knew this of course, but many of the calculations including PID, inverse and forward kinematics, and VMC are far easier to do in floating point than fixed point. It is much harder to make a mistake during development, and I hadn't run into any issues.
In addition, I am running FreeRTOS on the SAMD21. The control loop, motion primitive (and VMC) calculations, and telemetry all are software timers. The control loop is 500Hz, and the motion primitive and telemetry are each 100Hz. Again, running control loops in software timers is not ideal, but I didn't have issues with position or velocity control. However, current control in most commercial systems is the fastest of the control loops. In fact, it was implemented in analog for most systems until fairly recently. With VMC, we have the extra challenge that the current setpoint must be updated at every re-calculation of the motion primitive. If this is not done often enough, the tracking will be poor. I had previously simply attempted to run the motion primitive calculations at 200Hz, but the system malfunctioned. It was not clear at the time what happened, but this implied I am running into computational issues.
To look into computational issues, I set up an external pin to toggle low then high, wrapped around code of interest. I can then look at the signal on my oscilloscope to see how long sections of code are taking. The first one I looked at was the motion primitives software timer callback. This section has varying computation time since it supports linear or quadratic Bezier curves (which are not calculated in constant time), and both position and VMC tracking. For this profiling, I was running quadratic Bezier curves with VMC tracking. As seen in the image below, this calculation took about 1.88ms.
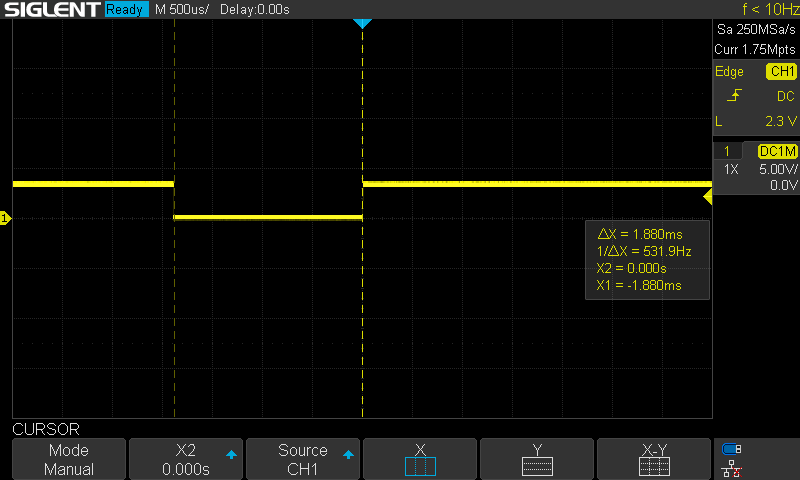
I then looked at my control loop. Again, this is not constant time. Here, we are in VMC current control mode. This was much faster than the motion primitive callback, only requiring 236us.
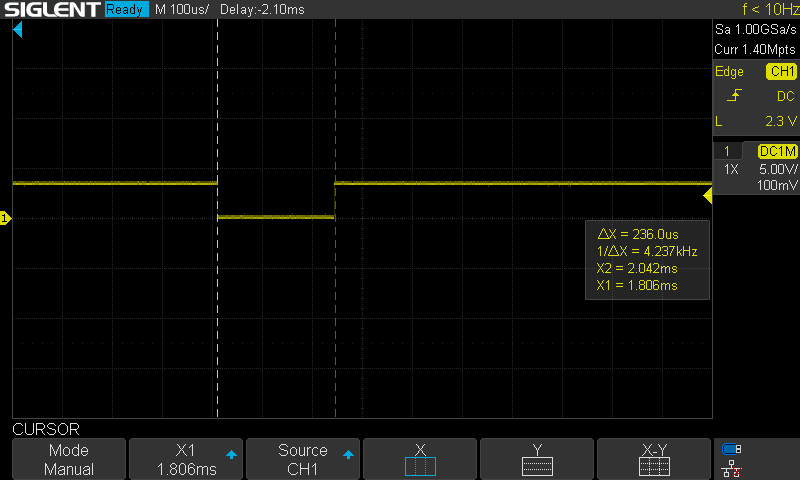
More telling was the timing consistency of the control loop. At 100Hz there is clear lag in the calculations, and two control loop cycles are bunched together. This 100Hz matches up to the rate of the motion primitive calculations, and since that can require almost 2ms (the period of the control loop), this is likely interfering with the control loop.
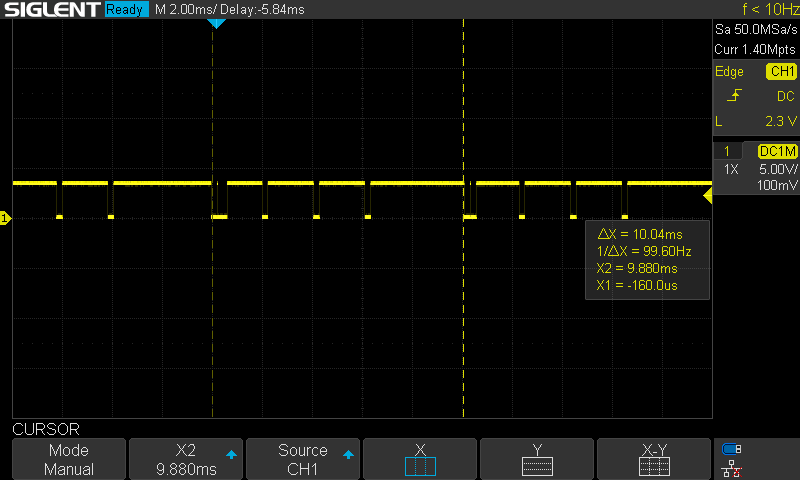
To complete the initial measurements, I also profiled the time required to add the telemetry CAN messages to their queue. That only required 124us, and is unlikely to be an issue.
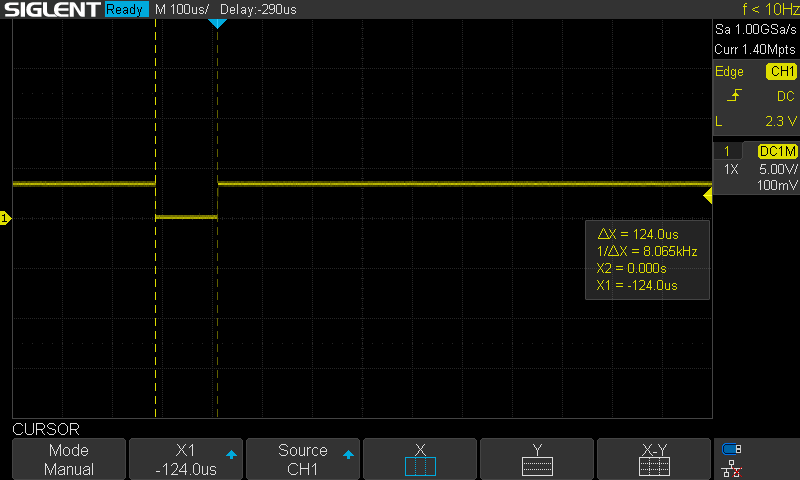
So, we know the motion primitives timer callback is too slow. The first step to improving its speed is to better understand where the slowdown is. That timer callback performs two main steps. First, it calculates the desired Cartesian foot position via a quadratic Bezier curve. Then, it calculates the VMC. I wrapped only the VMC calculations, and that section required about 1.56ms. Therefore, it is the clear initial focus. My first suspicion was the trig functions needed for the forward kinematics and the Jacobian calculation. I had been using the arm_sin_f32 and arm_cos_f32 functions within the forward kinematics, but I changed back to standard sin and cos from math.h. With only 4 trig function calls changed from Arm's versions to the math library, the time increased up to 2.43ms.
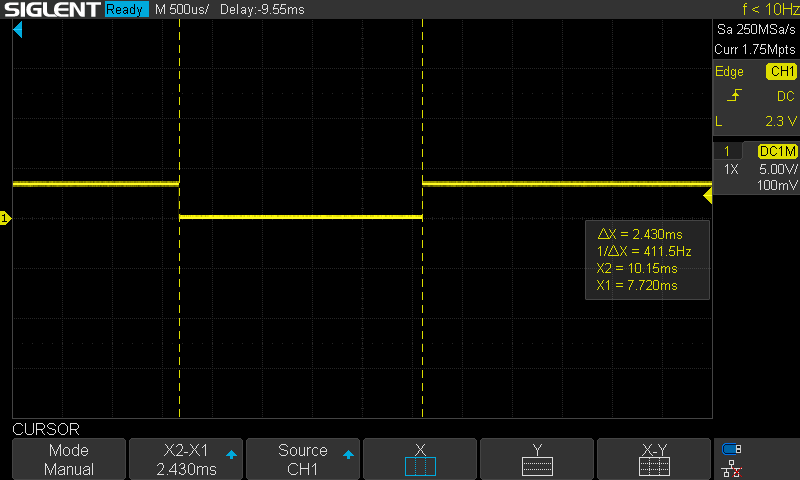
Clearly, we should use Arm's faster trig calculations. I also noticed that my Jacobian calculation was using sin and cos. Further, those calculations were identical to those performed within the forward kinematics. I therefore created a single function that also calculated the Jacobian.
void calculate_fk_and_jacobian(leg_ik_t * leg, pos_cartesian_t * pos, const pos_joint_space_t joint_angles, jacobian_t * j)
{
// Optimization, avoid calculating sin and cos functions twice
float ct = arm_cos_f32(joint_angles.thigh_angle_rad);
float st = arm_sin_f32(joint_angles.thigh_angle_rad);
float ctk = arm_cos_f32(joint_angles.thigh_angle_rad + joint_angles.knee_angle_rad);
float stk = arm_sin_f32(joint_angles.thigh_angle_rad + joint_angles.knee_angle_rad);
pos->x = leg->thigh_length_m * ct + leg->calf_length_m * ctk;
pos->y = leg->thigh_length_m * st + leg->calf_length_m * stk;
j->j_01 = -leg->calf_length_m * stk;
j->j_00 = -leg->thigh_length_m * ct + j->j_01;
j->j_11 = leg->calf_length_m * ctk;
j->j_10 = leg->thigh_length_m * ct + j->j_11;
}I also did some more minor optimizations, like pre-calculating the inverse of the gear ratio so that a floating point multiply is used instead of a division. These combined brought the time down significantly, to about 1ms.
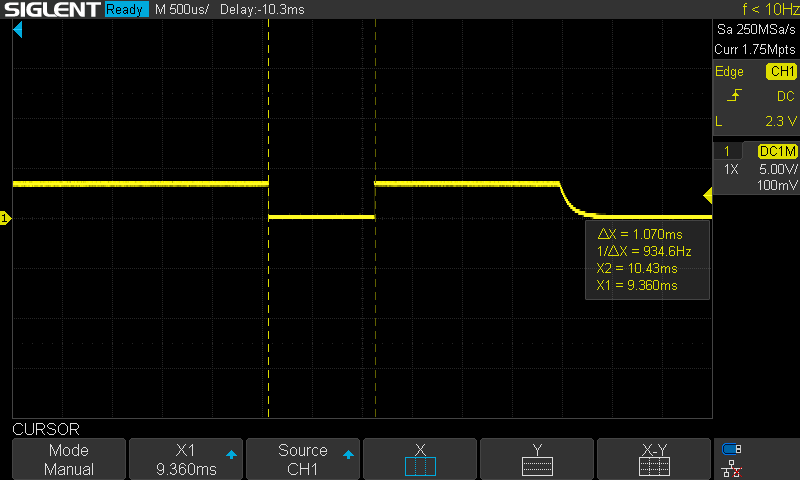
Finally, there is one section that calculates the foot's Cartesian speed using a difference and low pass filter within the virtual model controller. This is required to calculate damping. However, as a test I commented that out. Now the total time dropped to about 0.764ms.
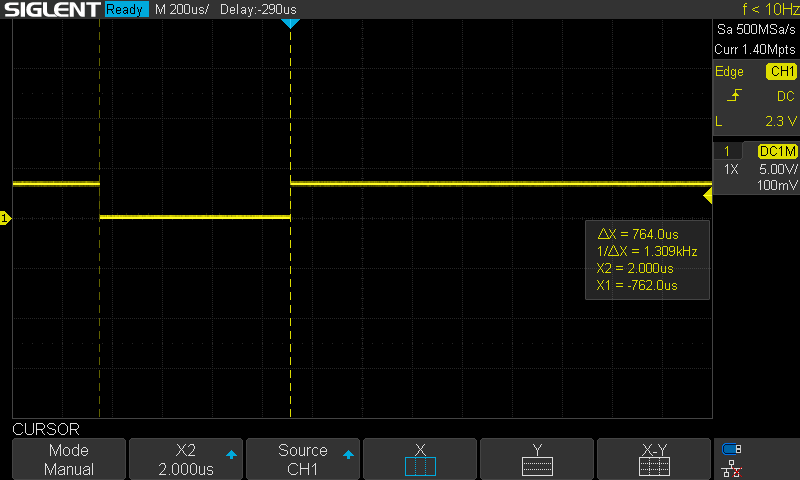
So, without any operational changes, we can get the time down to about 1ms and with some code removal (that could be replaced in integer math) down to 0.764ms. While this helps, it is unlikely to allow significant loop speed increases. Therefore, I think to get better VMC performance, we need to go faster. For this there are a few options that I am looking into in parallel:
- Set up current controller to be only integer math
- Setup control loop on hardware timer
- Or hardware timer triggering super high priority task to take over
- Shift parts or all of motion primitive calculations to integer math
- Design and build new version with FPU (I am doing another unrelated board with a 168MHz STM32F4 with FPU as my first experimentation with the STM32 line)
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.