One of the primary goals I have for this project is to cut paths for myself and others into the deep forest of abstract insights that researchers are accumulating in the science and mathematics of life. Art is able to do that because it can be slippery, amorphous, and enveloping at the same time - all properties of poor science. Its subjective interpretation is what makes it amorphous and allows it to slip out of the grasp of any one critical perspective. And yet art has the potential to completely modify the trajectory of a person through the world. That world itself can only be illuminated by science, but the perspective we see it from can be modulated by art.
Before this particular art project is modulating any perspectives usefully I've got to find my own way into the forest of research that has grown deep over the last few centuries around the topic of the nature of life. If I make it through then every path that is not the one that leads directly to the goal will eventually be reclaimed by the forest; maybe including the one I'll describe below.
Bashful Watchmaker
Building artificial life simulations is a paradoxical pursuit. In research the work is often motivated by profound wonder at how the unbending and unsympathetic laws of physics can spark and nurture life without deus ex machina appearing to simplify the story. And here in this art project my motivation is the same. But if there are gods then maybe they get a good chuckle out of the struggles of artificial life researchers. Though we dismiss watchmaker Gods as boring plot devices we are doomed to write them implicitly into any story we may hope to tell. That's the nature of the first basilisk I need to kill in making this project.
The first simulation I'm trying to write myself out of is meant to communicate one of the both surprising and potentially fundamental ideas about the nature of life that I can't stop thinking about. In line with the overall theme of this project the medium is meant to be an "embodied simulation" - in this case a digital simulation of artificial life running in a "robot" that couples it to the outside world. In this context by robot I mean a computing system that affects and is affected by the real world.
I've spent a long time thinking about the question, "is there anything profound to be found in such a system?" My intuition said yes but it has taken a long time of thinking about it to be able to pin anything concrete down with words. I want to take a jab at that right now knowing full well that it's a naïve attempt. I invite you to point out how in a comment.
Life Predicts Its Own Existence

"Simulation" has connotations of complexity that are obscuring so I think it's better to talk about games. Anytime you have rules about how information changes over time you have a game a.k.a. a simulation (as I mean it here). The rules of chess tell where you are allowed to move the pieces on the board. The locations of the pieces on the board is the information that the rules apply to. But chess is not very interesting as just rules and information. If it were just those parts then I should be able to describe the rules of chess to you and then say, "now you can derive every possible game of chess," and you would thank me and put the complete totality of chess up on a shelf in your mind. You wouldn't need to actually play any games and access any instances of the information about where the pieces are on the board - what would be the point? How the information, the location of the pieces, changes over times follows precisely from the rules. Another way to look at the issue is from the perspective of compression. If you want to describe the entirety of chess to someone you could either tell them the rules, e.g. "a bishop moves any number of vacant squares diagonally...", or equivalently you could describe where each piece is at every move in every possible game of chess. Obviously telling someone the rules, whether in an English description or computer code, is going to take way less time than painstakingly describing every possible game of chess. You could say that the minimal description of the rules is the optimal method for compressing chess, and the description of every game of chess is least optimally compressed.
Now take that idea and apply it to another kind of game: our universe. It also has rules, which are the laws of physics, and information they apply to, which is the positions, spins, charges, etc. of all of the particles and other fundamental bits that make up physical reality. Same as with chess you could imagine two equivalent descriptions of our universe at different ends of the compression scale. One is just the rules and the other is the state of the universe at every moment in every allowable timeline. Again it's obvious that the description of the rules must be far smaller than full telling of every possible history of the universe.
A lot of physicists in the last two centuries believed that if they had the rules of the game they could tell you the possible futures with absolute certainty. But there's a crucial difference between an agent "outside" the game trying to describe the possible futures of the game and an agent embedded "inside" the game trying to do the same: We imagine that the one outside can have perfect knowledge of the state of the game. They can see the positions of the chess pieces on the board. With perfect information the rules of the game can be applied with perfect certainty. But for an agent "inside" the game the information that they have access to may be limited by the rules of the game. That is certainly true for us in the game we are embedded in. We may eventually be able to derive a complete theory of physics, but we already know that the rule set we are being played with limits the information we have access to. One well known example is the uncertainty principle in quantum mechanics, which fundamentally limits the information that we have access to at the same time in physical systems.
Think again about the game of chess. It's a game that we made, that we are outside of when we play it, and one in which we have perfect knowledge about where the pieces on the board. Hypothetically two people who sit down on either side of a chess board could just sit there and stare at the pieces in their starting positions, imagining every game that they may hope to play against their opponent. Why then does anyone go through the motions of playing it? The obvious answer is that we've left out a critical part of any game: the players. It's not just the rules that make up a game of chess, it's also the actions that the players decide to take. Together two players plot a path through the space of possible games, exploring it with every move they make.
But why do the players play? Obviously they get enjoyment from the experience, but where does that come from? I would argue that it is fundamentally derived from pitting a guess about what is going to happen in the game (what move the other player is going to make in the case of chess) against what is observed to happen. Every life form from viruses to humans is always playing games at many different levels. A human that plays chess is still playing the game of natural selection at the same time. To be good at either it helps to be able to predict the future. A good chess player knows what moves the other player is allowed to make but can also guess what moves their opponent is likely to make.
In general any agent performs better if it has a better internal predictive model of the world. This basic idea is popping up in fields as diverse as biology, psychology, economics, and machine learning. Where this concept gets spooky is in relation to that fundamental limit about what is knowable that was touched on above. If a player can have perfect knowledge of the state of the game and its rules then there is no need to form a predictive model. Similarly, if the rules of a game are perfectly random then there is no way to even form a usefully predictive model of the game because there would be no pattern to whether a particular guess about the future turns out to be correct.
If you think about the space of all possible games and organize it based on how well future states of the game can be predicted from past states you would see the perfectly random game on one extreme end and games that always have the same outcome on the other end. Somewhere in the middle is our universe, and chess. I would argue that a fundamental property of life that we might find in any of these games is some ability to "predict the future". There's a sort of embodied version of that idea in the sense that, for example, in our universe our bodies are consistently "predicting a future" where they still exist in roughly the same shape. That sense of it may take a bit to chew through but there's another equivalent version that's a lot more teleologically palatable: every day we humans make predictions like, "I'll starve if I don't eat some food," that allow us to keep living. We make predictions and plans based on those predictions that allow us to gather the resources required to keep living. The opposite kind of thing is a cloud of gas that is very random. That kind of system is not easy to predict. There aren't any structures in it that the universe favors with predictive power - the particles jump around at random.
If you know even a little bit about modern physics then you probably know that we have started talking about entropy, which can be taken as a measure of disorder. The laws of thermodynamics say that on the large scale the universe gets less ordered over time. But in the context of that space of all possible games we shaped earlier there are games where that is not true. In a sense the games that are perfectly predictable have entropy constantly fixed at zero and the games that are purely random have it fixed at a maximum. But in our universe the rules of the game lead to entropy decreasing over time in isolated systems. In a way it's like our universe itself is moving from one extreme end of the space of games to the other, starting next to the chaotic worlds and ending at the perfectly predictable ones.
However, there's a caveat to the laws of thermodynamics with respect to entropy that becomes clear when thinking about life. Life necessarily represents a well ordered system, and in our natural history it seems to have created more order over time. How is that allowed in a universe where everything must get more random over time? The key is that entropy talks about isolated systems and the trend towards equilibrium. In systems that aren't at equilibrium, like the Earth basking in the flow of energy from the Sun, entropy can go up or down. In human science this subject area is known as non-equilibrium statistical mechanics. For this discussion you can interpret those words as saying: not being at equilibrium allows for life, statistics is a set of tools for dealing with prediction when the rules of the game do not allow for certainty about the outcome, and mechanics addresses what the rules are and how they are applied.
Going back to the notion that predictive power is a fundamental property of life, what we could argue is that entropy is a kind of knob that modulates the challenge life has in trying to predict its own existence. When entropy (disorder) is higher the only predictive models that work are like the person that tries to enumerate every possible game of chess. There's no way to boil all the information down to simple rules that are right often enough that they persist. Because life is embedded in the game that it is trying to play the rules have to be written down within the game. For a highly random universe that's very unlikely because it's both hard to write down the rules and the rules you would need to write down would be extremely verbose (i.e. it's not possible to compress the perfectly verbose description of timelines). Conversely in a universe with entropy at zero has only one "answer", one prediction that is always right, because nothing is changing. That universe is maximally compressible and there is only a single predictive model that will ever be right.
Here is where we get to the meat of the surprising and potentially fundamental aspect of the nature of life. When turning the knob of entropy somewhere there is a sweet spot where there are a lot of options for predictive models that work, and it's possible to efficiently write them down inside the game. When it's easier to write down the rules it's easier for autopoiesis to happen. And when there are lots of predictive models that work well it's easier for the resulting life systems to persist.
Making a Game That Plays Itself
I know the medium I want to use is an embodied simulation but I am struggling through finding the exact form it should take. It's incredibly easy to lose focus and muddy the message. I love jumping around between disparate ideas but too often that leads to communicating them in a half-baked way that doesn't let any one in particular have an impact on someone engaging with the work. To counter that I'm trying to take things slow and at least get to a point where it feels like there's a solid argument end to end that a project should exist before jumping into building anything. But if I do that forever I'm not making art I'm just being an unpublished researcher.
So I've been spending my time 90% researching and 10% building things. There are a few attractors in my chaotic system, which are specific materials or technologies that I have decided to use just because they feel interesting. One of these is a particular hardware gadget that I've been holding onto for years now. It's a classroom gadget that was designed to be used by students to answer pop quiz questions. Each device has a CPU, a screen, a keyboard, and a radio for communicating quiz answers back to a host device. I latched onto it as a potential material for a project because it was very cheap and bountiful for a moment. I snatched up 30 of the devices for very little money and assisted in some community reverse engineering of the device but then left them gathering dust in the corner of my studio.
I thought of them again while working on this project because they are a fairly convenient hardware platform for a swarm and my early thoughts on the kind of simulation I wanted to make involved a swarm of robotic agents. But since then my thinking has evolved and I've gotten fixated on a particular capability these devices have: they can communicate with each other unreliably over a distance.
Communicating With The Future You
Communication over a noisy channel is a compelling property for the fundaments of an artificial life simulation in the context of the discussion of the predictive nature of life outlined above. That became clear to me after I read a very fascinating paper called "Information theory, predictability, and the emergence of complex life" by Luís Seoane and Ricard Sole.
In the paper the authors try to capture the basic dynamics of life in an information theory context that is conveniently pinned in a way that makes it easier to consider the implications of the model. Hopefully they have done so without compromising its relevance to real life. That is not clearcut to me yet, but I find their arguments compelling.
In the paper they imagine "guessers" which are little machines that move along a tape of 1s and 0s like a Turing machine, except at each position they try to guess whether the tape will have a 1 or a 0. If they guess correctly then they are able to send a message to a receiver, which is the guesser in the next generation. They incur a "metabolic cost" for attempting to send a bit and receive a reward if the bit is transmitted successfully. If they receive more reward than cost then they persist.
The tape the guessers are riding on is called an "environment" and it is a fixed length but it wraps around in a circle. The bits in the environment are perfectly random, but the fact that the environment wraps makes it predictable (you'll always see the same sequence if you go around and around). The guessers are dropped at a random position and do their work. There are a lot of possible ways to construct a guesser but the authors simplify things by only looking at guessers that have a specific guess, an n-bit string, which they will try over and over again. They further simplify matters by only considering guessers with guesses that are "optimal", i.e. the n-bit string that is the "best guess" for a particular m-bit environment. For example the best guess in a 1 bit environment occupied by 1 would be 1.
In a sense the environment constitutes a noisy channel that messages are being sent through. If the guesser performs well then its message (which is itself, the string it is guessing) is transmitted to its descendent, because it is successfully read out of the environment. But because the environment is random the guessers don't always succeed and that leads to noisy transmission across the channel. Shannon and his lot in the information theory forest have a lot to say about transmitting bits across noisy channels. I'll come back to that connection below when we get back to the quiz answering gadgets but for now it's fine to ignore this equivalence.
What is mind blowing to me is that with this extremely simple game the authors proceed to show that as one fiddles with the size of the guessers, the size of the environments, and the ratio of cost to reward the guessers can be made to exhibit dynamics that we often see when order emerges from complex systems. When the ratio of reward to cost is turned up past the point where any particular guesser (even the most simple 1-bit guesser that always guesses 1 or 0) will survive then the size of the guessers is a neutral trait so there will be no particular trend towards small or large guessers. But if the reward to cost ratio is tuned the other way then something strange starts happening. Bigger (more complex) environments favor more complex guessers (ones with bigger n-bit optimal guesses) over less complex guessers. If the guessers are allowed to move up and down the complexity scale of environments then eventually a steady state is reached where there is a population peak for each size of guesser at a particular size/complexity environment. The peaks are ordered such that those of the smaller guessers are located in the smaller/simpler worlds.
It's an abstract model and I'm not in a position to carefully judge whether its representative of our reality, but it does inspire a few profoundly interesting ideas. One is a potential answer to the question of, "why didn't nature stop when it got to the first single celled organisms if those were so good at reproducing?" The answer may be that the minimal reproducing life form may not be the optimal one for a given environment, and the optimal complexity of an organism for an environment depends on the complexity of that environment. Applying this idea gets complicated because there's no delineation of "environment" in our world. Is it the universe, the Earth, the ocean, or the cell that the virus has just invaded? Or all of the above in different measures? Personally I think it's likely that knowing what kind of environment you are in with certainty is another kind of fact that is unknowable.
Another interesting idea that falls out of this work is that complex organisms don't prefer simpler environments. In cognitive science this is an answer to the dark room problem. Simply stated it's the question, "why don't organisms prefer predictable environments?" Why don't we eschew the challenges of navigating the world and instead go into our room, turn out the light, and wait for our death? If the nature of life is about predicting the future into existence then it would naturally seem like the easy answer would be for life systems to seek predictable environments. But the observations of the bitwise guesser world in this paper demonstrates a fundamental reason why that isn't the case. Life of a high complexity in a simple world will find itself out-competed for resources by simpler organisms. If it has the chance to move up the complexity gradient then it will do so in order to find the environment too complex for the competition but simple enough for it to survive in.
Finding Poetry in Bit Strings
My aspiration is to realize these abstract ideas in an aesthetically interesting physical system. The bit guessers' world does its job well in the context of research but it doesn't have any color and it is highly abstract. What are equivalent systems that possess other kinds of compelling beauty? I don't know any answers to that question, but I've been stumbling around an answer and have some work to share.
The basic plan is to run an artificial life simulation on the quiz answering hardware. Each organism would have a visual representation on the device's screen that evolves over time based on the simulation dynamics. Crucially the visual complexity of their morphology needs to be proportional to their internal complexity. The organisms running on each device reproduce by transmitting themselves over radio to other devices. The noisy channel from the bit guesser world therefore ends up interpreted literally in a fallible radio link. On the other side of the channel they need to read themselves into existence by using an internal model to overcome the random failures of the radio channel. But the nature of the random failures of the radio link are meant to vary in order to end up with "environments" (radio channels) of different complexity that the organisms can move through in a way that is equivalent to the migration of the bit guessers that end up congregating in environments with optimal complexity. I have some notions about how to achieve the varying of the complexity of the channels/environments but I'll leave that subject for a future post.
If the resulting system achieves equivalence to the bit guesser experiment where the guessers are allowed to find their equilibrium along the complexity gradient then in a long chain of these devices physically ordered by the complexity of their channel I expect to eventually see an obvious gradient of organism complexity. The simpler organisms would work their way downward towards the devices with simpler channels (or die out) and the more complex ones would move the opposite way.
But what would the organisms look like? Here's where I'm currently distracted.
Reaction Diffusion
If you are interested in this general space of ideas then you've probably come across the concept of reaction diffusion. Maybe like me a few days ago you have a vague notion of what they are and how they work but have a vivid memory of what patterns reaction diffusion can form. They show up everywhere. So many have written about them elsewhere so I won't here but I'll link to the best explanation that I have come across.
I was thinking about ways I might get interesting dynamics and morphology together with a simple system and remembered these reaction diffusion models. I decided to try implementing them in Houdini myself and mix them in with another rich space I've played with before - Verlet integration-based constraint solvers. Here's what I ended up with:
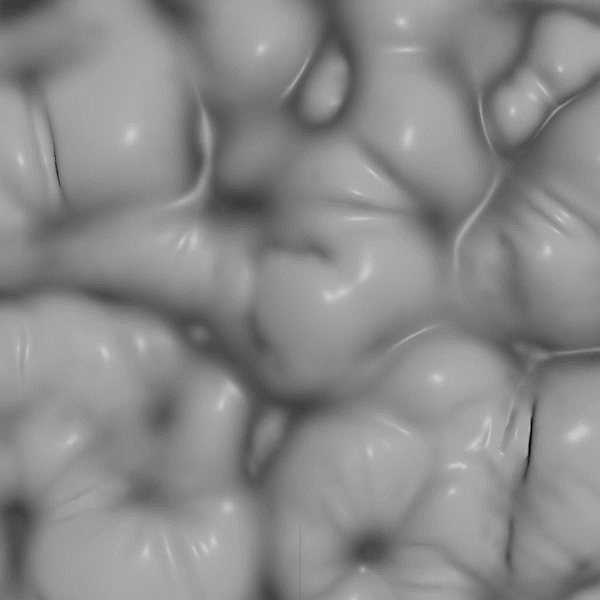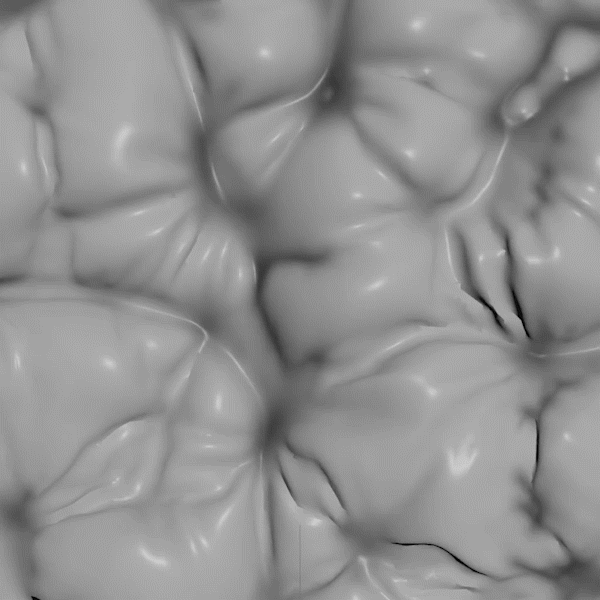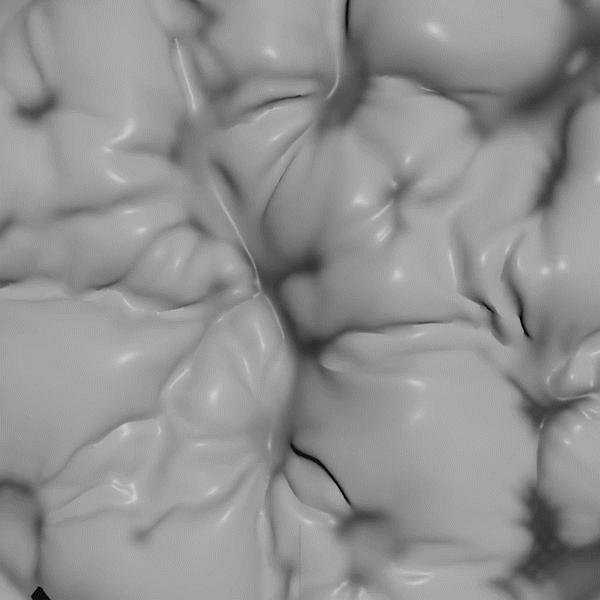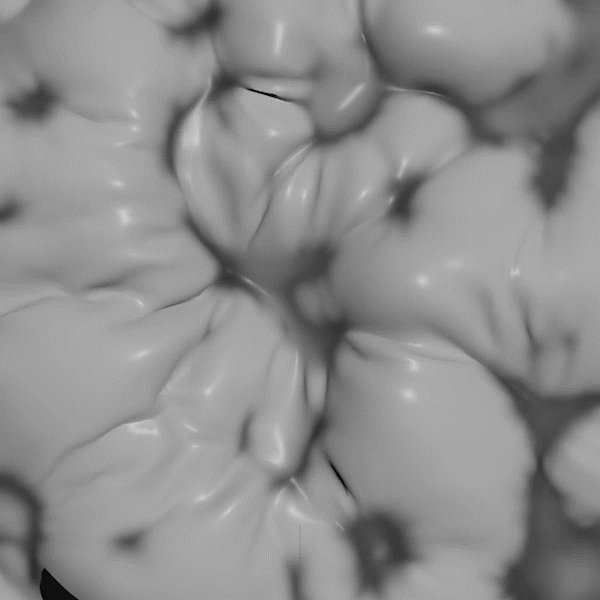
My reaction diffusion system runs on any mesh using the vertices as the tanks where the reaction is happening, and the edges as the path for diffusion. The constraint solver also runs on any mesh and initializes with a length constraint for every edge. To couple the two systems together I modify the rest length based on the concentration of one of the reactants. With the right parameters you get the behavior above.
It was an interesting experiment to do and very educational for me but this kind of result is well within tired territory of computational geometry. I'm very late to the reaction diffusion party.
I have seen other people play with reaction diffusion systems but I've never done so myself and now I'm realizing I was missing out. These systems are mesmerizing in their juxtaposition of simple rules with vast emergent complexity. I played around for many hours and in the course of doing that I started doing simple experiments varying the parameters of the reaction model across the mesh so that I could map out the dynamics of the system. These turned out to be way more interesting than expected.

I found this region and was struck by how it resembles a beach with waves slowly falling onto relatively static "sand". But in this case every point in the image represents a slightly different permutation of rules. One way to look at it is a metaphor for the space of possible games that I described above. The bottom is made of highly disordered worlds that are hard to predict. The very top is made of low entropy dead worlds with one right answer to the question of the future (the same as the past). But the middle is occupied by an area hospitable to emergent complexity.
I don't yet know whether this inquiry into the results of coupling reaction diffusion models to a geometric constraint solver will yield fruit that I can transmute into the bodies for my version of the guessers. We shall see! I'll leave you with one more image that was sculpted by me rather than discovered:
 Owen Trueblood
Owen Trueblood
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
This is fascinating. Really excited to see it develop.
Are you sure? yes | no