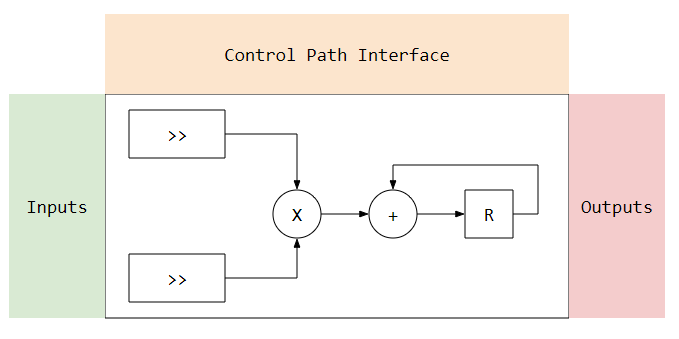
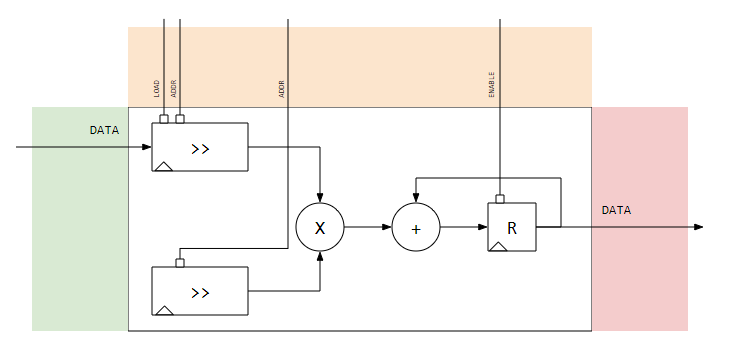
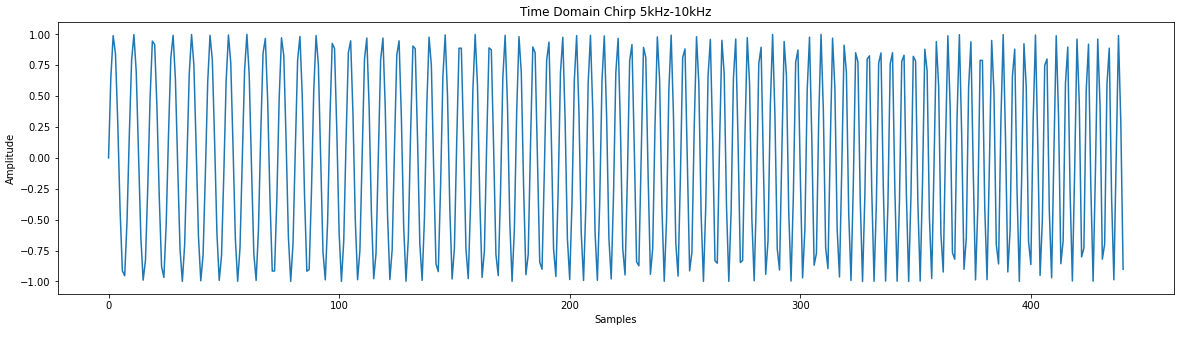
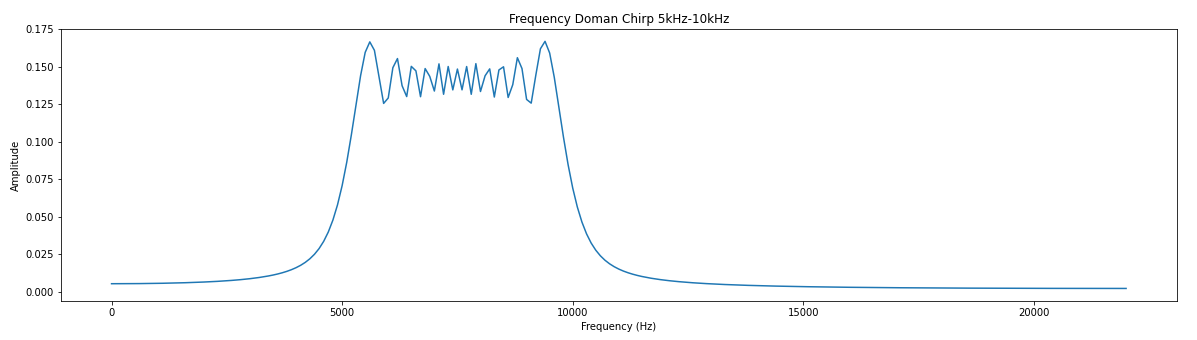
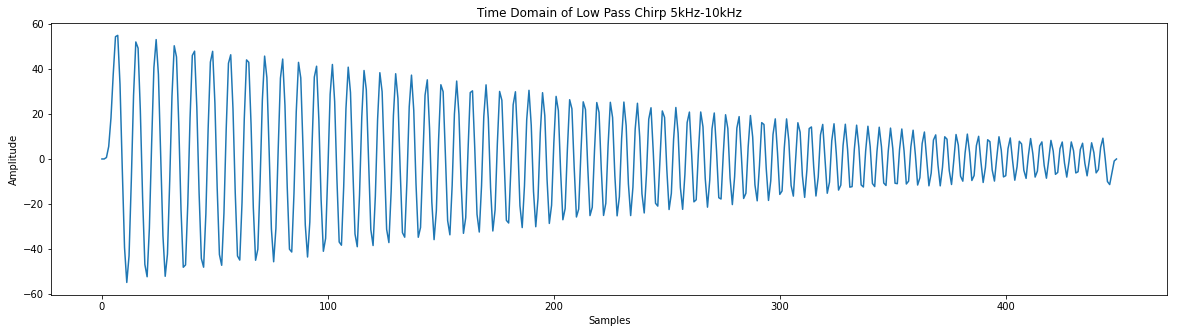
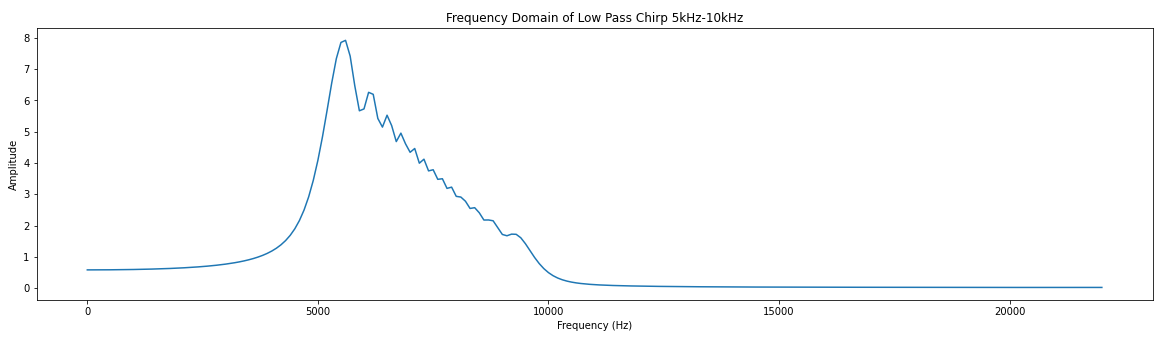
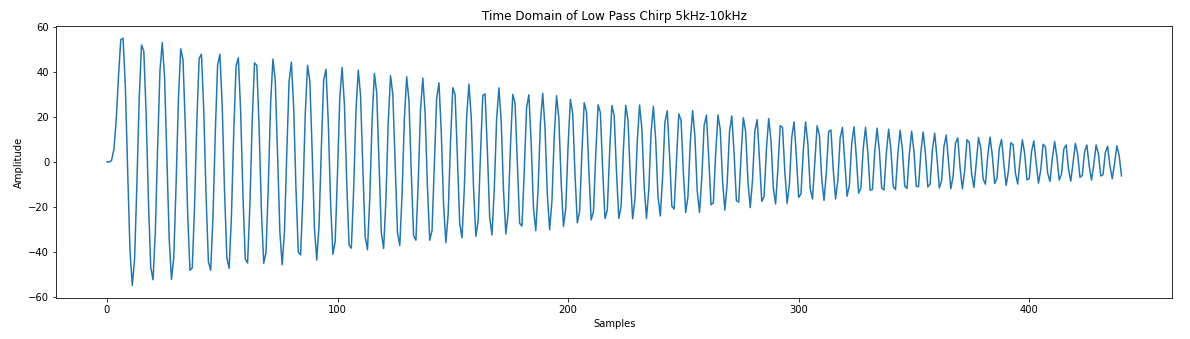
We are trying to create a simple digital filter. I call it simple because:
- It has 10 coefficients.
- The coefficients are fixed
- No concurrent arithmetic
I'm using python to create software models and VHDL to create the hardware models. I'll use Cocotb to verify the hardware models. I will target Digilent's Basys3 FPGA board to run the results.
 Jake R.
Jake R.



 Electronx
Electronx
 schlottmachine
schlottmachine
 Kuldeep Singh Dhaka
Kuldeep Singh Dhaka