Para la generacion de trayectorias:
Se necesitan poder cumplir los siguientes requisitos:
- Conocer la geometria y disposicion de cada pata con respecto al marco inercial (el centro del hexpaod)
- Poder hacer la cinematica directa para poder determinar las matrices que describen la orientacion y la posicion (la pose) del efector final
- Poder determinar el Jacobiano de Posicion para cada pata para poder hacer una funcion de Cinematica inversa
- Poder Realizar un algoritmo de cinematica inversa que pueda tomar como entrada una serie de puntos que describan una trayectoria, y poder guardar los angulos de cada junta para toda la trayectoria en un array para poder mandarlos atravez de un microcontrolador
Conocer la gemetria y disposicion de los componentes
Esta parte es relativamente sencialla considerando que solo se necesita poder tomar las medidas de los componentes desde el modelo 3D. Tomando las medidas para una pata y las medidas de la base a una de las patas exteriores obtenemos:
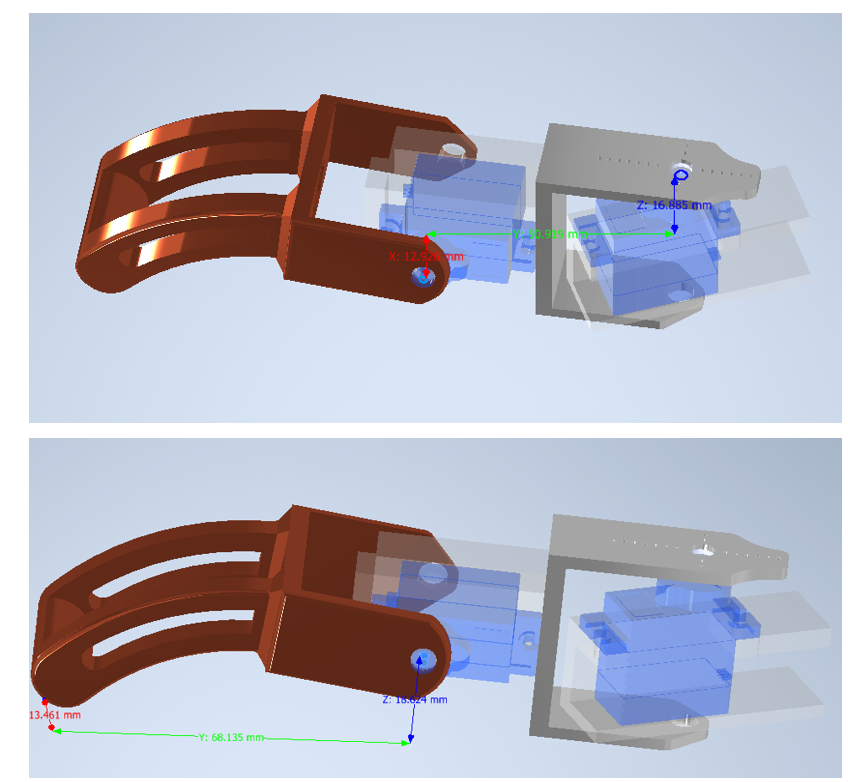
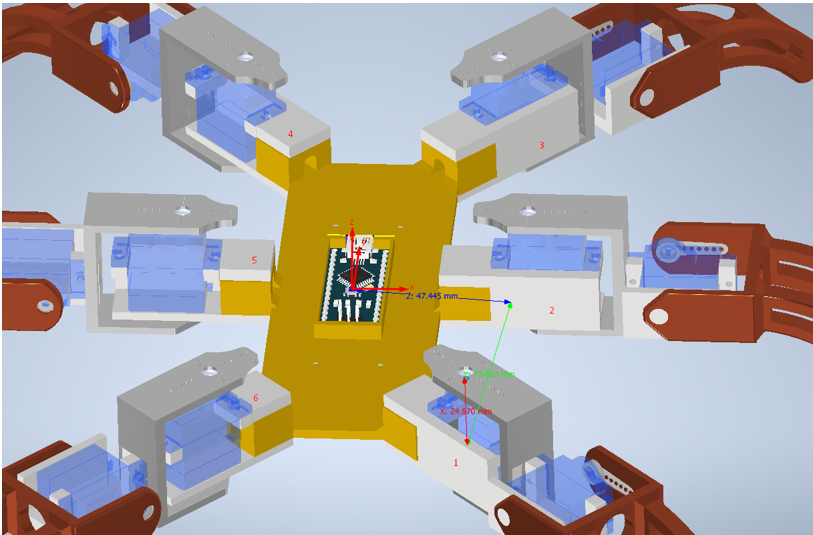
*En esta imagen se indica elorden de las patas como se consideraron en programacion
Con estas medidas podemos proceder a fabricar la matriz DH para iniciar el calculo de la cinematica directa
Cinematica Directa
Para poder calcular la cinematica directa, podemos utilizar un algoritmo que nos calcule la matriz de transformacion apartir de la Matriz DH.
Con los valores de distancias y las rotaciones de 90 grados para un servo y el otro obtenemos la siguiente matriz DH apartir de Dos transformaciones A1 y A2:
A1:

A2:
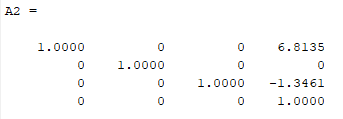
Donde DH = A1*A2:

Con esa matriz DH podemos luego utilizar transformaciones de base para obtener la cinematica directa de cada una de las patas. Las transformaciones de Base permiten ubicar las patas en el espacion, donde el centro del hexapodo representa el punto (0,0,0).

Una vez ubicadas las Piernas, para obtener su matriz de transforamcion solo hace falta obtener la multiplicacion de Transformacion de Base x Matriz DH. Aprovechamos a obtener la cinematica directa, que dado un punto inicial (q1, q2) nos devuelve las posiciones en XYZ:


Los valores en Rojo representan las coordenadas X, Y, Z para la pata 1 cuando q1=q2=0.
Ya con la cinematica Directa, podemos proceder a calcular El jacobiano para utilizar una de las definiciones de cinematica inversa
Cinematica Diferencial:
En este caso se utilizaron algoritmos discutidos en clase para poder obtener el jacobiano para cada pata. Sin embargo, debido a que cada pata es identica, solo era necesario obtener el jacobiano de una pata para describir tanto el cambio de posicion y velocidad de las demas. En este caso en particular, ya que se habla de movimientos coordinados, solo era necesario el jacobiano de posicion
Se obtiene una matriz n*6, donde n = numero de juntas (que en este caso son dos)
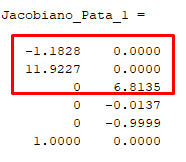
Donde solo nos interesan los primeros 3 valores.
Con esto dicho podemos usar la pseudo inversa del jacobiano (ya que no es una matriz cuadrada) para determinar la relacion entre coordenadas y los angulos de las juntas.
Cinematica Inversa:
En este caso en particular, se utilizaron quaterniones para poder calcular la cinematica inversa de posicion apartir del jacobiano de la matriz de transformacion. Esta cinematica inversa solo calcula los angulos para un solo punto.

El algoritmo utiliza transformacion de valores en quaterniones, cuyas propiedades matematicas nos permiten calcular la pseudo inversa de mejor manera sin necesidad de utilizar otros metodos por aproximancion

De esta manera, utilizando calculo iterativo para aproximarse lo mejor que se pueda dado una tolerancia de error que se da de antemano.
Con esta funcion, el programa nos regresa lo siguiente para las coordenadas (0,0,0) de la pata 1:

Donde el primer valor corresponde al angulo q1 del primer servomotor y el segundo valor corresponde al segundo angulo q2 del segundo servomotor. Todo segun nuestras coordenadas globales
Generacion de Trayectorias
Para poder generar una trayectoria utilizamos el comando 'mstraj' para converir un vector de puntos una matriz 3x3 con coordenadas x,y,z que ejecutan se mueven de un punto a otro creando asi una trayectoria.

Con los puntos escojidos, Se obtiene la siguiente trayectoria
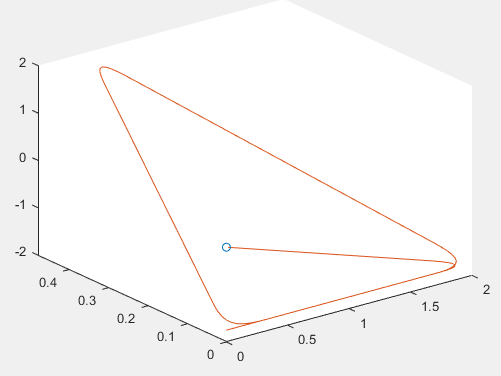
La figura de la trayectoria para las piernas de un hexapodo o inclusive un cuadrupedo debe de aparentar ser una semi-elipse. Esto es que la pata se mueve en movimientos circulares mientras que en una mitad del momimiento se impulsa hacia adelanta y en la otra mitad del movimiento se levanta del suelo apra regresar a su posicion original. De tal manera se pueden intercalar los movimientos de las patas para lograr secuencias de movimientos que impulsen el haxapodo o que lo hagan rotar. Debido a la disposicion de nuestros actuadores, todas las patas solo necesitarian una misma trayectoria, solo que para las patas del lado izquierdo, esta trayectoria tendria que ser invertida para poder encajar con la secuencia de movimientos que se requerian.
Con los puntos definidos e la trayectoria, podemos utilizar nuestra funcion de cinematica inversa en un 'loop' que genere angulos para todos los puntos de la trayectoria.

Aqui el codigo ejecuta la cinematica inversa para los angulos de cada servo, pero dado que todos siguen la misma trayectoria, solo guardamos los angulos para ambos servos de la primera pata. Dado que hay que poder ingresar estos 'arrays' en un programa que pueda ejecutar un microcontrolador, hayq que poder guardarlos como un archivo de texto. Considerando tambien que este programa se va a correr en un Arduino nano, utilizando la librerira Servo.h necesitamos redondear los valores y pasarlos de radianes a grados.

Ya con los arrays de angulos, lo unico que se necesita es probarlos en un simple programa .ino de arduino y hacer los ajustes necesarios.
Programa de Arduino:
Aprovechando el uso de la libreria integrada de Servo.h Podemos proceder a definir cada uno de nuestros actuadores. Utilizamos un formato donde J1= servo conectado a la base y J2 = Servo conectado a la pata. Donde les agregamos una extension de P'N', donde N corresponde al numero de pata donde estan conectados.
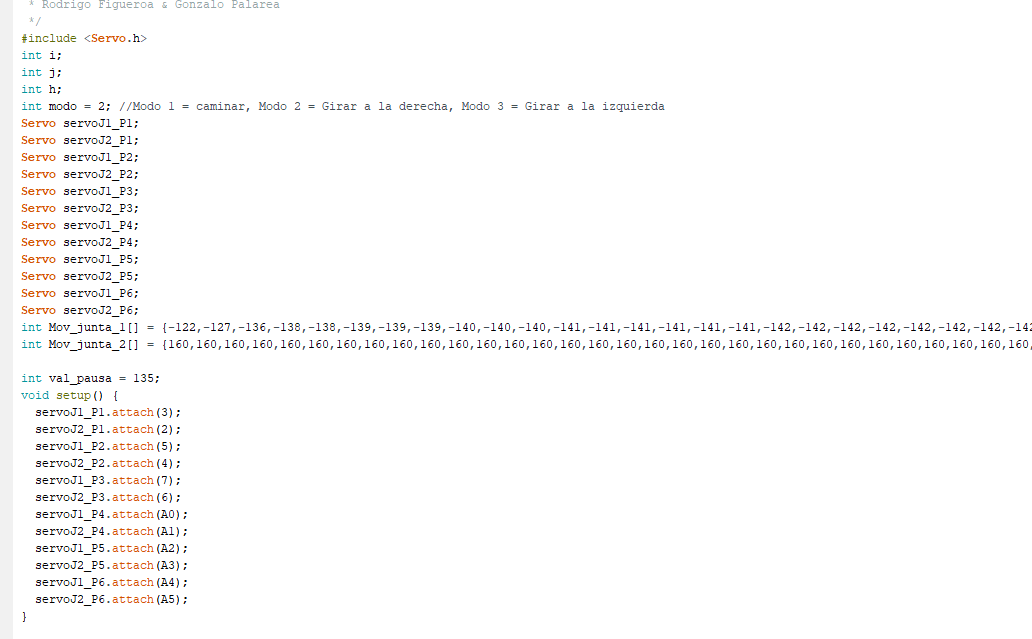
El comando 'attach' sirve para definir el pin del arduino al que estan conectados. Como se puede ver en los arrays de 'Mov_junta' definimos los angulos que debe de tomar el servo a lo largo de su trayectoria. En este caso solo se tienen dos arrays, dado que nuestro hexapod cuenta con 2 GDL para cada pata y usamos la misma trayectoria solo que en un orden especifico para cada grupo de patas.

De lo investigado, para hacer que el robot camine hacia adelante o atras, se deben de mover dos patas de un lado y una pata del lado opuesto. Para las patas 4-6, hubo la necesidad de invertir la trayectoria para ajustarse al movmimiento de las otras dos patas. Esta trayectoria sin embargo, puede ser obtenida directamente de el archivo de MatLab. Encontramos que reducir la cantidad de variables en nuestros expermientos nos dio mejores movmimientos. Para conseguir que el hexapod rote, solo se necesita que se muevan las tres patas de un lado mientras que las otras tres patas permanecen estacionarias. Se pueden ver unas sumas y restas de angulos en las patas para corregir la manera en que la pieza plastica estaba montada en los servos.

Utilizando esta subrutina, logramos que el hexapod caminase hacia adelante, rotara y luego caminara hacia atras como se puede evidenciar en el video del resultado final.
Movimientos:
*Notese que incrementamos el delay en los movimientos para que se pudiese apreciar el movimiento de cada pata.
Girando:
Caminando:
Resultado Final:
 Ricochetrj
Ricochetrj
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.