Following the previous log An individual job and all the necessary processing, I wrote the program gold_01.c to check the behaviour before I increase parallelism.

First thing it did was confirm that the result C=1 occurs only when the result X=0. So we can save/ignore this data point.

Let's now look at the output for the smallest job: w=3

1 6 6
2 0 11
3 2 5
4 5 3
5 3 4
6 4 5
7 7 35

This one is quite weird because 7 loops back to 7 in 35 cycles but we can follow the primary loop easily :

1 -> 6 -> 4 -> 5 -> 3 -> 2 -> 0

And since 0 is reached with C=1, it goes back to 1 in 7 crossings (and 29 steps, w3 is clearly asymmetrical).

From there, it's very easy to script for the other sizes.

$ for i in 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
 do echo -n "$i: "
    gcc -Wall -DWIDTH=$i -Os gold_01.c -o gold
    /usr/bin/time ./gold > job_$i.log
 done

3: Total: 69
0.00user 0.00system 0:00.00elapsed 91%CPU (0avgtext+0avgdata 1424maxresident)k
4: Total: 269
0.00user 0.00system 0:00.00elapsed 87%CPU (0avgtext+0avgdata 1384maxresident)k
5: Total: 797
0.00user 0.00system 0:00.00elapsed 93%CPU (0avgtext+0avgdata 1392maxresident)k
6: Total: 4157
0.00user 0.00system 0:00.00elapsed 94%CPU (0avgtext+0avgdata 1428maxresident)k
7: Total: 16079
0.00user 0.00system 0:00.00elapsed 90%CPU (0avgtext+0avgdata 1368maxresident)k
8: Total: 23114
0.00user 0.00system 0:00.00elapsed 90%CPU (0avgtext+0avgdata 1316maxresident)k
9: Total: 258059
0.00user 0.00system 0:00.00elapsed 0%CPU (0avgtext+0avgdata 1320maxresident)k
10: Total: 1049597
0.00user 0.00system 0:00.00elapsed 50%CPU (0avgtext+0avgdata 1388maxresident)k
11: Total: 4190147
0.00user 0.00system 0:00.00elapsed 83%CPU (0avgtext+0avgdata 1524maxresident)k
12: Total: 16781251
0.03user 0.00system 0:00.03elapsed 96%CPU (0avgtext+0avgdata 1548maxresident)k
13: Total: 67117049
0.08user 0.00system 0:00.09elapsed 98%CPU (0avgtext+0avgdata 1512maxresident)k
14: Total: 268451737
0.36user 0.00system 0:00.36elapsed 99%CPU (0avgtext+0avgdata 1624maxresident)k
15: Total: 1070073927
1.43user 0.00system 0:01.44elapsed 99%CPU (0avgtext+0avgdata 1928maxresident)k
16: Total: 4295032829
4.96user 0.00system 0:04.97elapsed 99%CPU (0avgtext+0avgdata 2396maxresident)k
17: Total: 17179997009
23.58user 0.01system 0:23.64elapsed 99%CPU (0avgtext+0avgdata 3352maxresident)k
18: Total: 68719736689
110.75user 0.03system 1:51.12elapsed 99%CPU (0avgtext+0avgdata 5528maxresident)k
19: Total: 274803255069
486.96user 0.11system 8:09.19elapsed 99%CPU (0avgtext+0avgdata 9612maxresident)k
20: Total: 1099443499868
1880.05user 0.36system 31:27.70elapsed 99%CPU (0avgtext+0avgdata 17692maxresident)k

Of course, past w16, the running time and the memory explode.

Interestingly, the number of total iteration quadruples for each increment of w but the total size of the file only doubles:

       44 10 juil. 00:50 job_3.log
      113 10 juil. 00:50 job_4.log
      251 10 juil. 00:50 job_5.log
      557 10 juil. 00:50 job_6.log
     1226 10 juil. 00:50 job_7.log
     2753 10 juil. 00:50 job_8.log
     5921 10 juil. 00:50 job_9.log
    12423 10 juil. 00:50 job_10.log
    27659 10 juil. 00:50 job_11.log
    58670 10 juil. 00:50 job_12.log
   122025 10 juil. 00:50 job_13.log
   264080 10 juil. 00:50 job_14.log
   559598 10 juil. 00:50 job_15.log
  1161492 10 juil. 00:50 job_16.log
  2449479 10 juil. 00:51 job_17.log
  5194057 10 juil. 00:53 job_18.log
 10763126 10 juil. 01:01 job_19.log
 22192296 10 juil. 01:32 job_20.log

The raw data (19MB) is available here if you don't want to spend 1/2h to compute the larger ones.

I visualised the output data with gnuplot. Here is a plot of the length of the arcs of w16:

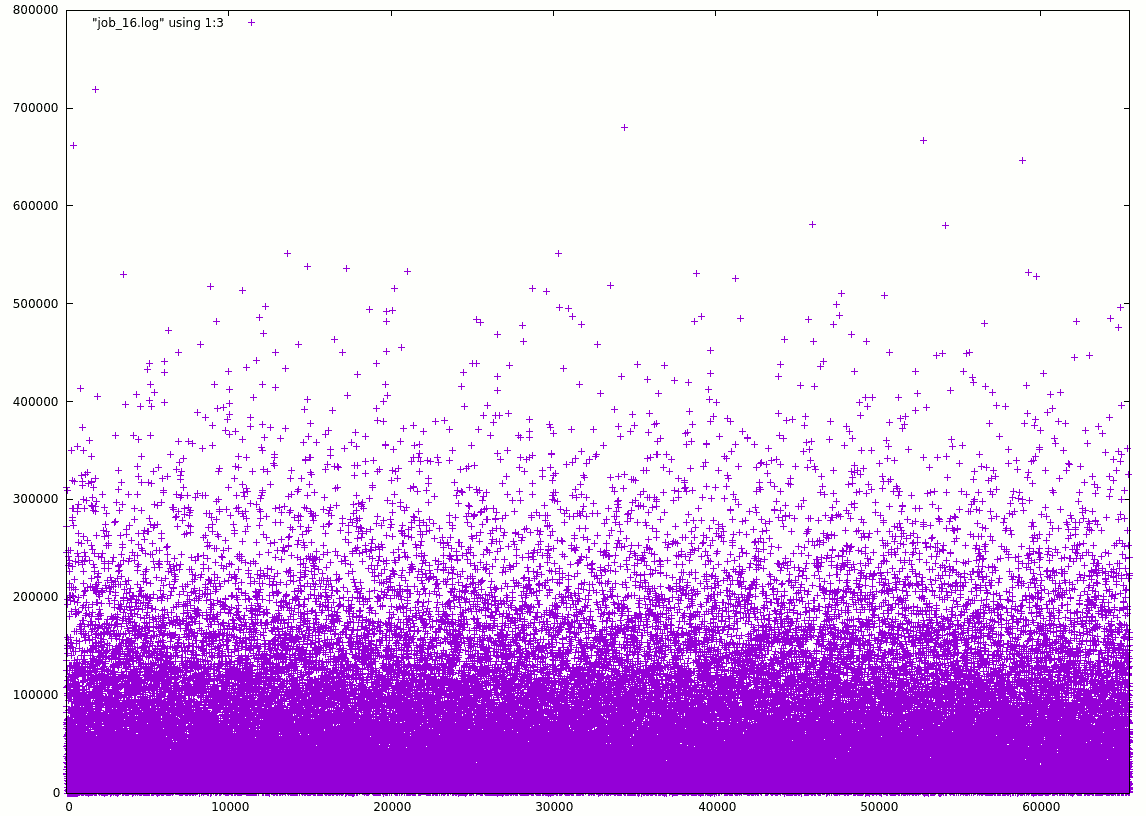
It looks quite random and the lengths range from 3 to 718818, or about 11× the number of arcs (that's not excessive).

Here is the distribution (obtained by sorting the lengths):

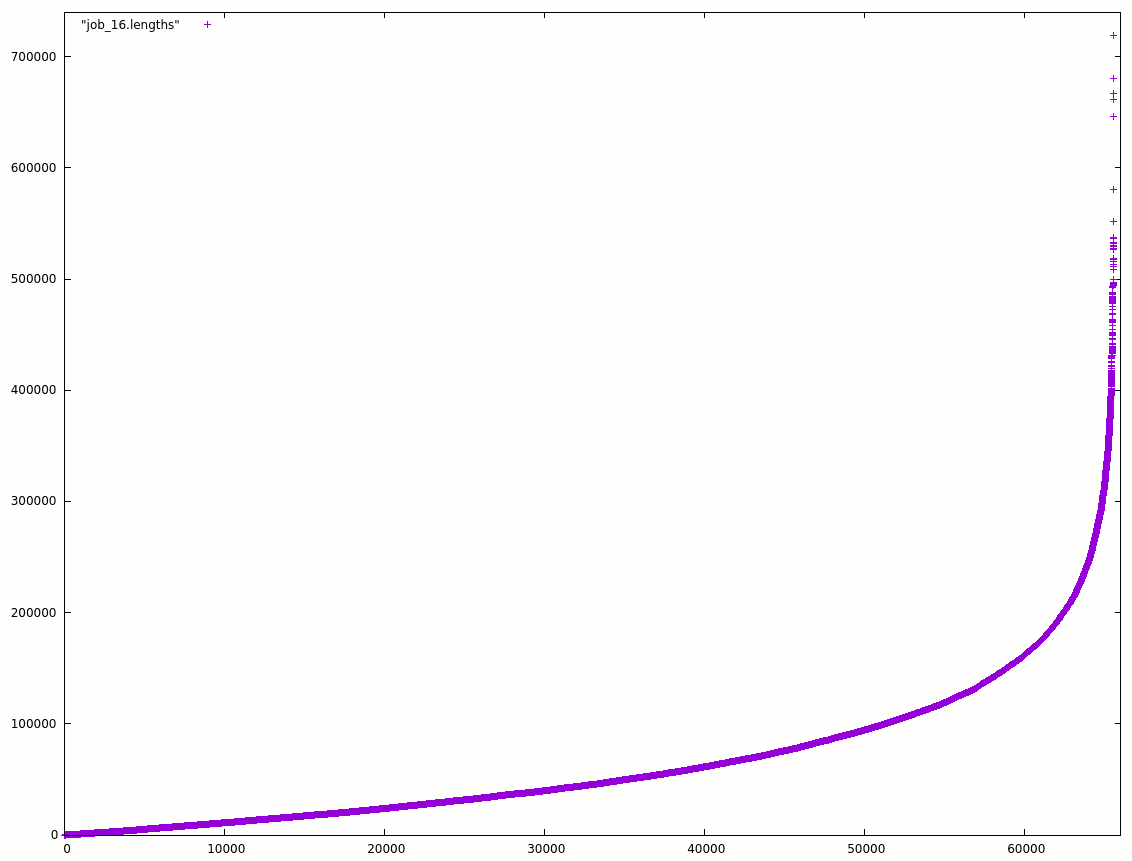
Does that make it an exponential curve ?

Half of the arcs are shorter than 45000, or about 2/3 of the size.

Of the 65535 arcs, only 19746 are duplicates (about 1/3).

__________________________________________________

Let's see with w4:

1 7 23
2 11 6
3 13 42
4 10 14
5 14 9
6 15 14
7 8 10
8 9 3
9 4 31
10 2 20
11 5 8
12 6 34
13 12 25
14 0 10
15 3 20

There are 2 orbits:

Primary orbit:
1 -> 7 -> 8 -> 9 -> 4 -> 10 -> 2 -> 11 -> 5 -> 14 -> 0 -> 1 : 11 arcs
23+10+3+31+14+20+6+8+9+10+1 = 135

Secondary orbit:
15 -> 3 -> 13 -> 12 -> 6 -> 15 : 5 arcs
20+42+25+34+14 = 135

The sums match previous tests but we see that the number of arcs varies a lot.