In this project, we are now used to seeing the pattern of w4, as shown below. Go to http://ygdes.com/~whygee/PEAC/a2_07.html  to run it yourself.

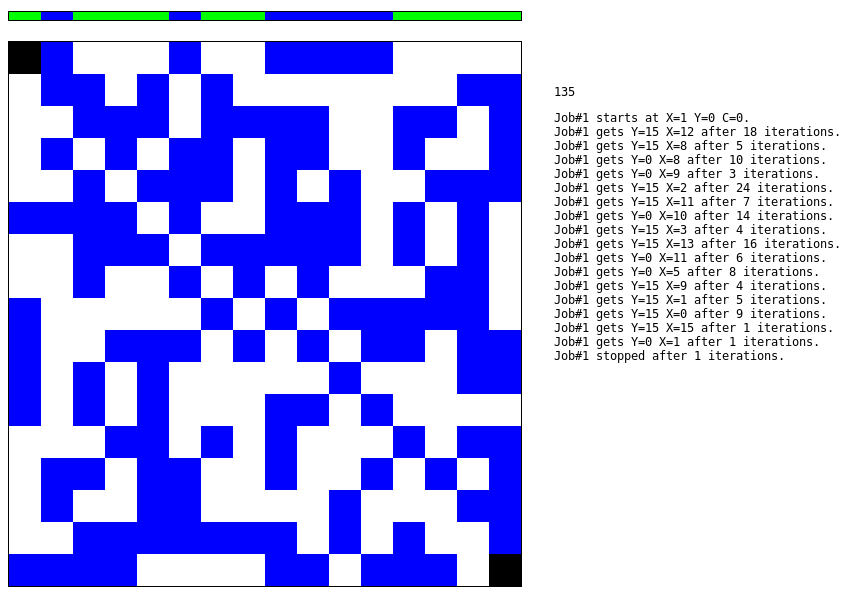
The list on the right contains all the "crossings", where Y=0 or Y=15 (or MASK in the code and other cases). The 135 iterations loop after 16 crossings, with semi-arcs
of the following lengths: 18, 5, 10, 3, 24, 7, 14, 4, 16, 6, 8, 4, 5, 9, 1, 1

Definition: Semi-arcs are like the previous arcs but they can end at Y=0 or Y=15

In the previous logs, we have explored and checked the "complementarity" of the dual orbits. Due to the central symmetry, we have X'=MASK-X, Y'=MASK-Y and C'=1-C. The orbits evolve strictly identically.

So it should make sense that, at any time, the coordinates could be "complemented" and the orbit's properties will not be affected. In the following code, the coordinates are complemented for each crossing where Y=MASK. Look for youself at http://ygdes.com/~whygee/PEAC/a2_07b.html

It works as expected even though to me it sounds counter-intuitive. But the numbers spoke. The patterns have changed significantly but the semi-arcs have the same lengths as in the original case. The central symmetry is still here, as well. It's uncanny but it's here.

The big improvement though is that both orbits are covered with only one orbit worth of computation. And ALL the semi-arcs start with the same Y value. This makes the scan 2× more efficient and this still gives the same results as if the 2 complementary orbits were scanned.

The "crossing" pattern is quite different from the original orbit but I have tested the equivalence with other sizes and the maths match again. Compare for W10:

http://ygdes.com/~whygee/PEAC/a2_06.html (normal)
http://ygdes.com/~whygee/PEAC/a2_06b.html (semi-arcs)

The simplification is significant for the scheduling algorithm. We don't have to check extra conditions: the new "semi-arcs" start at Y=0 and end at Y=0 or Y=MASK, Y is cleared during scheduling and the information can be discarded. Just don't forget to invert X of course.

From there the obvious consequence is simple: if all semi-arcs can be joined to a single loop to create one orbit then the width is maximal. We don't even need to count the lengths though they are useful for further studies and validations. The validation of this property has other far-fetching implications that will become obvious later, little by little...