I managed to make a C program work on my laptop, almost to completion. But after 7:42 minutes, I get a core dump :-/
[FiboSum]$ gcc -g -Wall orbits_fs16c2.c -O2 -o orbits && /usr/bin/time ./orbits Filling orbit 1 at 1,0,0 with 2147516415 iterations... Filling orbit 3 at 1,1,1 with 2147516415 iterations... 4294311453.76user 6.84system 8:47.86elapsed 87%CPU (0avgtext+0avgdata 8389976maxresident)k 0inputs+0outputs (0major+2097212minor)pagefaults 0swaps orbits[1234]: segfault at 7f9769ac9010 ip 00000000004009e2 sp 00007ffec75ebc60 error 4 in orbits[400000+1000]
WTF ? I suspect there is a problem with printf() but so far the results that were printed before the fault are amazing. The data show that there are only 2 orbits and the other states lead equally and directly to one of these orbits. So, unlike my past experience with degenerate LFSRs, there are not sub-standard values (except 0,0,0 which should never happen, but we have the carry input for this).
The conclusion so far is : you have roughly one chance in 2 to fall in one of the 2 equal orbits, otherwise you are one iteration away from one of these orbits. In other words, this algo is safe and close to optimal !
I only need to solve that segfault.....
-------
gdb tells me :
Program received signal SIGSEGV, Segmentation fault.
0x00000000004009d2 in trace_orbit (sX=sX@entry=65535, sY=sY@entry=65536,
sC=sC@entry=1 '\001', nr=5 '\005') at orbits_fs16c2.c:70
70 t = MAP[A];
and I see I did not clean my data properly, a word mask and it'll be solved.
...
There !
........ 8589737984 : o1:2147450879 o2:0 o3:2147450878 o4:0 max=1 orbits:5 8589803520 : o1:2147450880 o2:0 o3:2147450879 o4:0 max=1 orbits:5 8589869056 : o1:2147450880 o2:0 o3:2147450880 o4:0 max=1 orbits:5 NEW ORBIT closed after 1 iterations Closed ! The end. 7 Orbits Max. backtrack size : 1 Joins: 1 : 2147450880 2 : 0 3 : 2147450880 4 : 0 5 : 0 6 : 0 --------- 697.54user 3.62system 11:45.67elapsed 99%CPU (0avgtext+0avgdata 8389912maxresident)k
If you have more than 8GB of RAM, you can try the program by yourself.
The count of orbits is misleading but the program reminds us of the 2 blocking points : 0,0,0 (which is manually blocked in the program) and 0xFFFF,0xFFFF,1 (which I had forgotten and appears as orbit 6)
The two other orbits have a period of 2147516415 and are immediately joined by 2147450880 (2³² - 2¹⁵) single points, as inferred from the "Max. backtrack size = 1" : there are no longer trajectories than that.
There seems to be a high symmetry, with both orbits and their trajectories. I have a little idea of how/why but this will be for later, for now, I'm glad that this algorithm behaves better than expected.
You can download the program there : orbits_fs16c2.c.
The structure of the orbits is summarised in the following diagram :
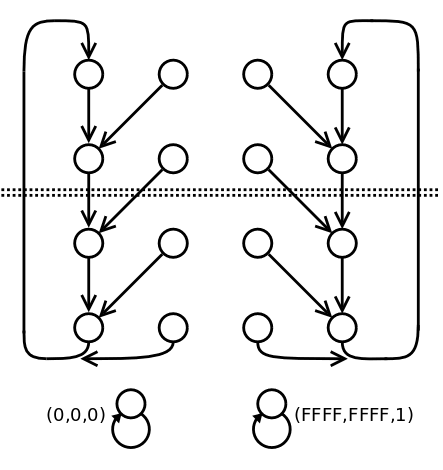
(updated)
 Yann Guidon / YGDES
Yann Guidon / YGDES
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.