This episode/project makes me really sceptical and confused. Maybe that's disarray.
I have seen that the Pisano periods have been studied for ages but I have so far never seen the algorithm that this project describes. As if it was original to even use a carry out into the carry in of additions. Or to loop over the successive results of additions, which Adler and Fletcher missed. I have found "Fibonacci hashing" but it's not related.
In fact I am already familiar with systems such as Bob Jenkins' lookup3.c which contains many additions and XORs so I didn't think it would be ground-breaking to minimise this type of system down to the purest, smallest essential ideas. I would expect this to have been already extensively studied as a primitive for other systems to build upon. I could imagine that this "primitive" is taught at the first year of secret cryptoschools, alongside LFSRs and Fiestel rounds. The Fibonacci generator is not perfect, but so are LFSRs which are so widely used instead. Maybe they could be combined ? (yes)
I feel lost, just as when I discovered the #σα code, the #µδ code, the #Recursive Range Reduction (3R), the Balanced Control Binary Trees, but I have also "rediscovered" or "reinvented" many things... And I have no idea how to find prior art or references on something that I just find, because, if it is really new, how can I know that it existed already or not ? Ignorance is not an excuse, so if you have any hint, idea, suggestion or data, please comment or contact me. I simply can't understand that such a simple system didn't exist before.
...
It is not easy to find resources about the subject of this project. When doing a websearch, entering the keywords "Fibonacci" and "LFSR" or "CRC" bring pages that compare the CRC topologies of Fibonacci vs Galois (or this very project).
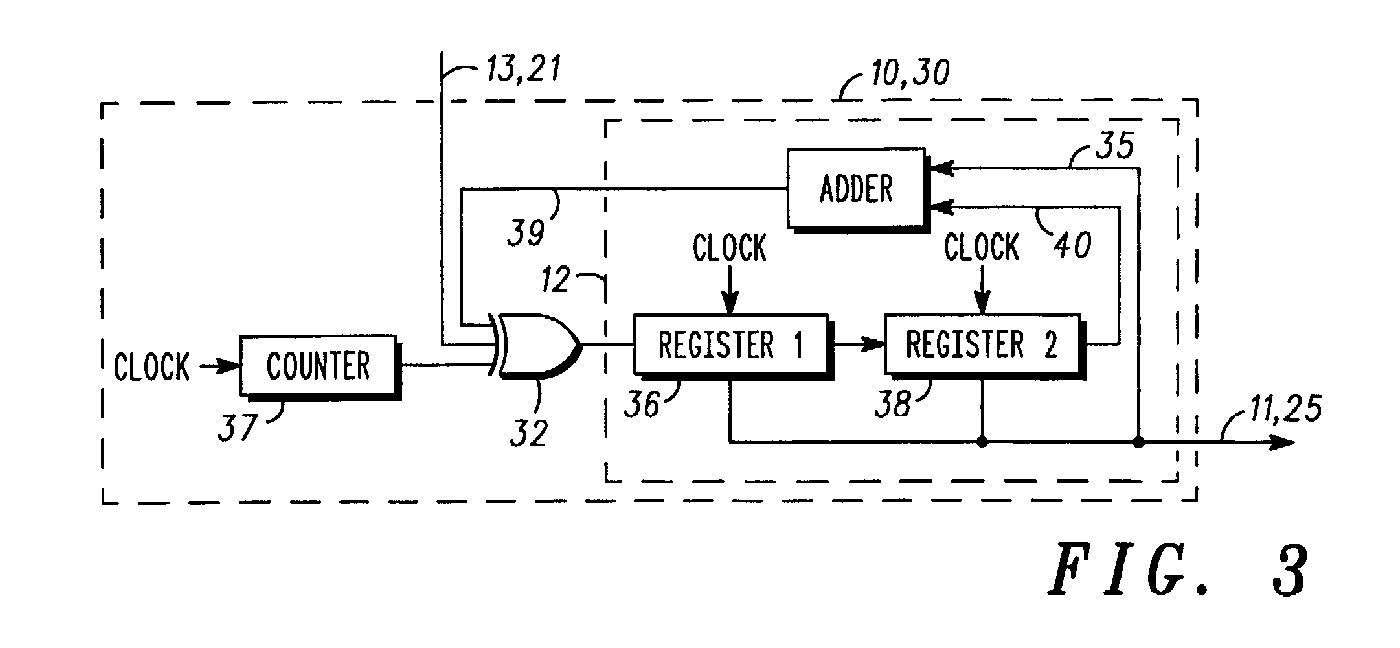
I have found something quite close but the claims are shaky and the patent has been withdrawn. Look at the figure 3 of GB2377142A : it has all the elements, and even more, but organised differently. For example, the XOR is in series with the output, which introduces the weakness discussed in an earlier log. The patent addresses this weakness by adding a counter (which could/should be a simple LFSR, as in Fig. 2), and since there is no carry re-circulation, this can be considered as a simple "Pisano" checksum.
...
Update:
An astute reader pointed me to https://github.com/endlesssoftware/sqlite3/blob/master/wal.c
The SQLite software uses a similar scheme, which closely follows the Piano Magic song mantra to the letter, but with 32 bits and with no carry, it's tuned for speed and not resilience but it seems to be "good enough":
** [...] The checksum is computed by interpreting the input as ** an even number of unsigned 32-bit integers: x[0] through x[N]. The ** algorithm used for the checksum is as follows: ** ** for i from 0 to n-1 step 2: ** s0 += x[i] + s1; ** s1 += x[i+1] + s0; ** endfor ** ** Note that s0 and s1 are both weighted checksums using fibonacci weights ** in reverse order (the largest fibonacci weight occurs on the first element ** of the sequence being summed.) The s1 value spans all 32-bit ** terms of the sequence whereas s0 omits the final term.
Can you hear Glen Johnson yet ? :-D (with Y=S0 and X=S1)
Combination/mixing occurs with addition and not XOR, the difference does not seem meaningful. The lack of carry recirculation however lets me think that the missing overflow recycling reduces the "safe block length" and exposes the algorithm to a "stuck point" situation. Which is why my first idea was to use only half of the register length to keep some extra entropy out of reach from incoming data tampering.
The file's date is 2010 and I suppose there were earlier implementations but what's the earliest one ? I'll have to track the author since the name is absent...
....
Another hint and find in this thesis dated 2006:
McAuley [29] has proposed the Weighted Sum Codes (WSC) algorithm as an alternative to the Fletcher checksum and CRC. Feldmeier [30] conducted a comparison of WSC against one’s complement addition checksum, XOR checksum, block parity, Fletcher checksum, and CRC. He asserted that WSC is as good as CRC in error detection and as fast as Fletcher checksum in compute speed. Because WSCs are not commonly used, we leave an examination of that checksum to future work.
Why is this paragraph interesting ? Because the code above mentions "weighted checksums", so "Weighted Sum Codes" or WSC might be the name previously given to this type of structure.
The thesis :
The Effectiveness of Checksums for Embedded Networks by Theresa C. Maxino
A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in Electrical and Computer Engineering
Department of Electrical and Computer Engineering, Carnegie Mellon University, Pittsburgh, Pennsylvania, USA, May 2006
The reference:
[29] A. J. McAuley, “Weighted sum codes for error detection and their comparison with existing codes,” IEEE/ACM Trans. on
Networking, vol. 2, no. 1, pp. 16–22, Feb. 1994.
Good, the date goes back to 1994 now. But if "WSC is as good
as CRC in error detection and as fast as Fletcher checksum in compute speed", WHY are they not commonly used ?
Anyway, this good read provides some very useful graphs, such as this one that compares XOR and ADD checksums :
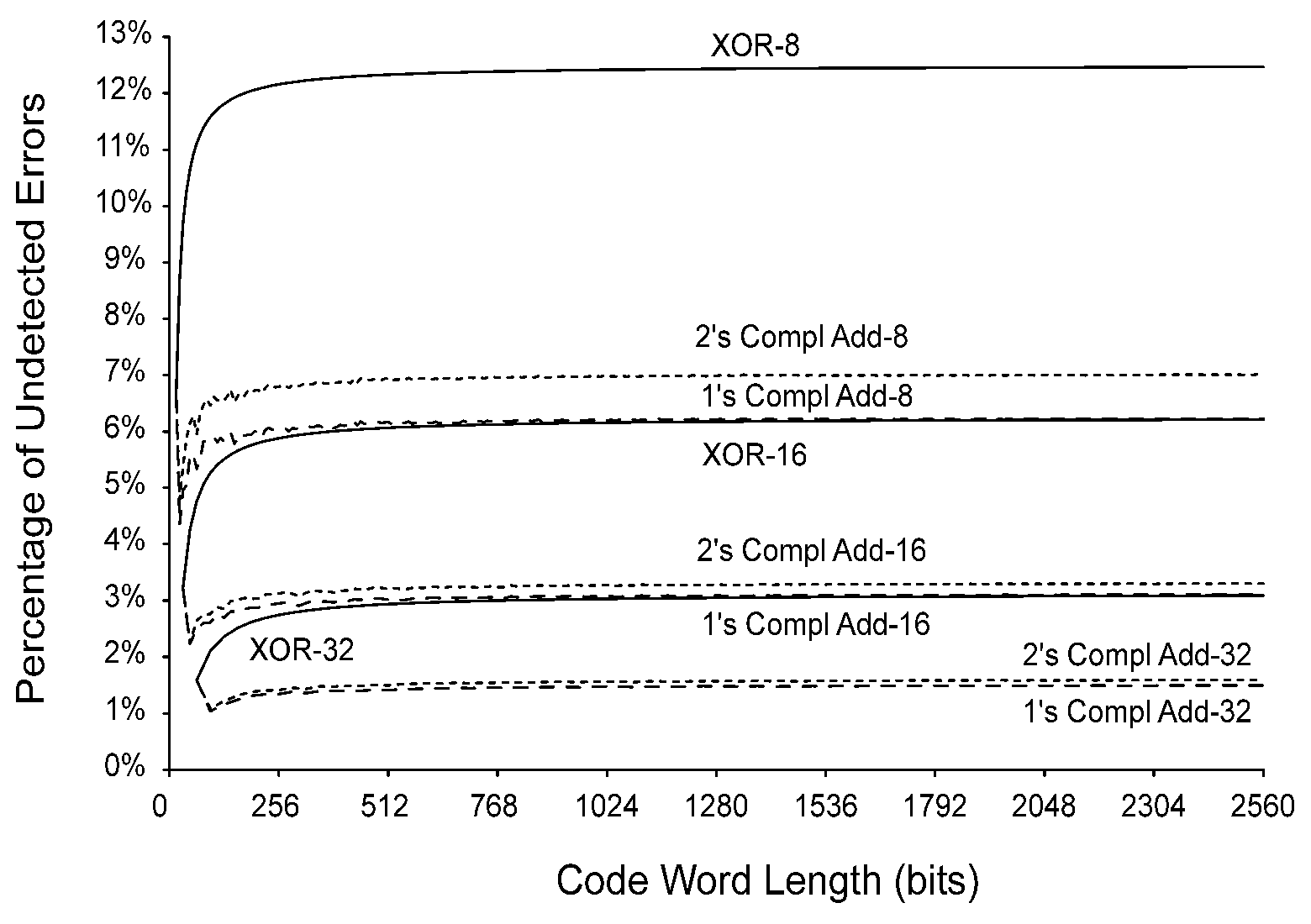
Asymptotic undetected error rates don't seem to go below 1% when 32-bit words are added together... Go and read the thesis for more of these graphs !
....
More weighted sum codes at :
Weighted sum code without carries — Is an optimum code with detection of any double errors in data vectors (good question)
Weighted sum codes for error detection and their comparison with existing codes (The 1994 McAuley paper is often cited)
McAuley filed at least one patent on using WSC while at Bell Labs. The patent US5526370A expired in 2014 and does not seem to cover what is studied in this project. I get the impression it performs a sort of circular rotation of the data...
.
...
Update:
I have received a personal message, which I try to translate here:
Aside from speed, what matters for checksum algorithms is the mathematical proof, for example the probability of collision, the guarantee of Hamming distance...
The checksums like CRC32 (LFSR-based) are interesting because their efficiency is quite easy to prove. Furthermore their hardware cost is low, and some processors have a carry-less multiply instruction. Hence I don't see the point in using anything else.
As we French say, "it's not false", but also incomplete. I will try to address each point and provide more context:
- Speed matters. A lot. We agree :-)
- Mathematical proof, and insight into how and why something work, is also essential. The logs of this project show how I went from a basic, classic Pisano approach to a much better system by simply using the carry, which is a "simple trick" that can be reused in other places. I believe there is more to learn from this variant but my past experience with CRCs has shown me what to look for first: I went for the "state map" and tried to characterise the "orbits". I'm used to this sort of behaviour which appears with LFSRs where the polynomial is not a "generator". As long as the orbit is relatively long, the memory of an alteration will remain, which is all we ask for from this class of checksum.
- Hamming distance, or the number of bits that differ, is not a consideration for crude checksums. Their results are short (8, 16 or 32 bits "only"), hence much much more sensitive to collisions than collision-resistant or crypto-strong algorithms. It is not meant to be a "hash" for indexing, or a tamper-proof digital signature. In ALL cases, one altered bit is enough to invalidate the block. While hashes and signatures have stringent constraints on confusion, diffusion, reversibility and others avalanche effects, checksums do not. So the Hamming distance for a checksum is not a consideration.
It boils down to your "error model" and/or BER (bit error rate). CRCs are favorites for serial communications (radio or wire, when you can't afford Turbo codes) where certain types of errors appear (they are listed in other documents). CRCs are also great for serial communications because the traditional implementations compute one bit per cycle, in sync with the data stream.
For a digital checksum, the context is very different. Data are parallel and the BER is low, the checksum is used for sanity and catch eventual glitches. For example, the well-known TCP protocol uses plain additions, with the (obsolet) option for Fletcher, which enhanced this a bit, and Adler enhanced it further for his Zlib. ZIP uses CRC32 but computing 8 bits at once requires a 1KB lookup table, which I have studied around 2006 before turning to Mersenne twister to avoid the problems with Pentium-class CPUs (while ZIP was tailored for the 8086 generation, with no alignment and masking constraints). - Which leads me to this : today, few processors (quantity-wise) have the "carry-less multiply instruction". It is rare and requires intrinsics because it is not supported by most languages or compilers (except Intel's ?).
- Meanwhile, IP still uses the plain old additions to checksum the packets. Because it's just enough, the BER is usually low, it works with the appropriate error model (lower-level devices manage bit errors and other trivial tasks) and even if it is flawed, this is less important than the other benefits, in particular the ease to modify the checksum when a network node modifies the packet en route.
- As noted before, the hardware cost of CRC is low only if you deal with serial streams. It's a few XORs and a string of DFFs, some buffers, and you're flying. However, in the context of checksums, data streams are parallel and again, carry-less multiplies are still far from everywhere.
- When one designs a new algorithm that they wish to be widely adopted, they can't expect much more than what the C language provides, which is also a requirement when defining encryption/decryption algorithms (see NIST constraints in their calls for applications). Today, specific accelerating instructions may only be reasonably used inside platform-specific libraries to provide a boost to an application. But this is not an option for many basic embedded systems for example, like network appliances, which often employ sub-standard cores and SoC to save a penny on the Bill of Material.
When you create a portable program, the end user simply expects to get the source code, compile it and run it. Some #ifdef and autoconf could provide specific shortcuts but you can't expect any platform to provide any exotic function outside of the set offered by the 1965-era PDP-7 that served to create UNIX and C. It's sad but it's a constraint, which in turn has shaped and even restricted CPU architectures since : for example MIPS (and its evolution RISC-V, as well as many RISC platforms such as Alpha) have no carry hardware because only assembly language can expose it. POWER stands out, though. Gone are the "decimal adjust" flags or the parity flag from the 70s era microprocessors. Which computer language provides a native "parity" function ? - Finally, " I don't see the point in using anything else." could be another example of "when you have a hammer, everything looks like a nail". It is very widespread, it is comforting and helps you get things done quickly. Personally, I try to expand my toolbox of algorithms so I can use the best tool for each case, and every discovery increases my chances to work better, or increase efficiency with fewer efforts here or there. Furthermore, CRC have well-known limitations, such as the "forbidden state" with all bits cleared.
- I will also mention the difficulty of ultra high speed hardware parallel CRC for very dense polynomials, because this creates a crazy forest of XOR gates. Some implementations must split the computations in two steps going through intermediary polynomials, which is far from trivial. The CRC of the defunct PATA standard (precursor of SATA) was 16-bits wide only and the polynomial was "very sparse" (only 3 coefficients IIRC, I couldn't find the documents again) to keep the hardware small. Yet it was not for a serial link, so the seemingly sub-standard CRC poly was "good enough" to work at 66MHz and spot alterations due to transients, cable reflections or clock issues.
So the nuance I try to explain is that the context, the constraints, the goals, will guide the choice of an algorithm: the more we already know, the better. And there are many cases where you will simply use an existing library (particularly for sensitive applications where you can't afford a bug or a leak). But this is not always possible (for all kinds of embedded systems) and this is where knowing more primitives helps.
In the case of the 2×16bits primitive I characterise in this project, the point is that it is "good enough" for many trivial tasks where security or safety are not critical, but resources are very scarce. The "Pisano with carry" approach is a very low-hanging fruit, it is not perfect in every aspect. If you want a better result, you can combine it with other imperfect algorithms, so their defects cancel each other, like I did in 14. Moonlighting as a PRNG.
If more statistical properties are required, http://www.burtleburtle.net/bob/hash/doobs.html is a great introduction (and the whole site is a goldmine). I also remember that Bruce Schneier's "Applied Cryptography" book has in-depth analysis of LFSR/CRC and some exotic derivatives that tried to solve LFSRs' shortcomings.
 Yann Guidon / YGDES
Yann Guidon / YGDES
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.