The robot can control the bow angle of attack using metal gear motors. A stepper motor pulls the string and arrow back, and a servo releases the bow to shoot.
The real technical challenges here is with the computer vision system and making sure all that high school physics on projectile motion was right. The camera I used was the Intel RealSense Depth Camera D435i, a pretty expensive piece of hardware. However, the cost paid off because the hardware did all the hard work. The camera easily found color and depth of an object, so a target that is say bright red or green it was easy to find that object. Data from the camera allowed me to find the targets pose, or position and orientation.
The bow I used was a cheap kid bow I found on Amazon, but this bow had a really important function in that it had a guide for the arrows motion. That was important because I did not want the arrow going all over the place inside the bow. Next, I modeled the little toy arrow as a spring, and was able to calculate its spring constant. Using that number, I was able to calculate the arrows initial velocity using energy conservation.
Now with the position of the target and the ability to control the initial velocity this problem became a simple projectile motion.
Math behind everything:
Bows Spring Constants:
I used a force gauge to measure the bows draw weight at different positions and used linear regression to get the bow string's spring constant.
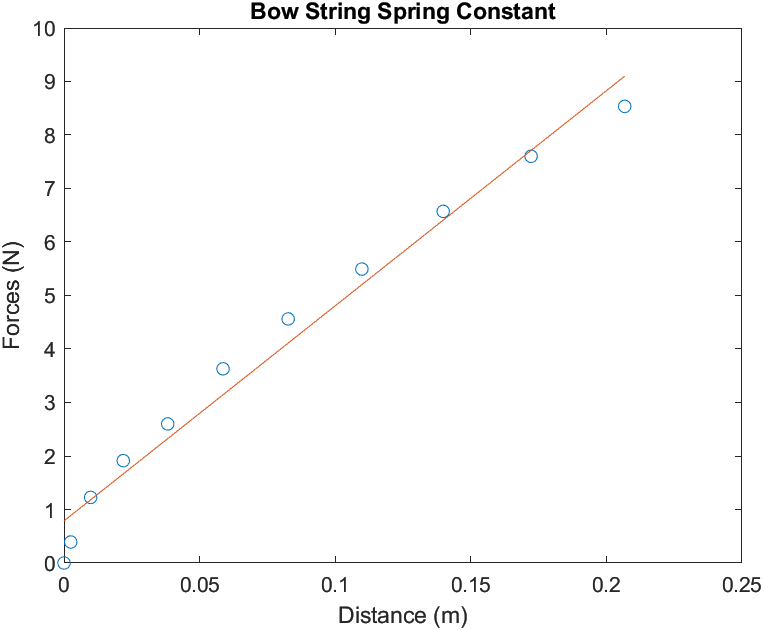
The slope of the line of best fit is the spring constant.
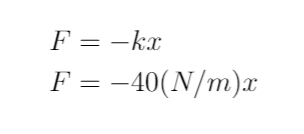
Conservation of Energy:
Now that I had the spring constant I could solve for the arrow's initial velocity by know the energy is conserved from the bow string's potential energy to the kinetic energy of the arrow upon release.
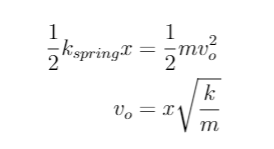
Projectile Motion
As the arrow is in flight its going to move in a parabolic curve. I want to control the shape of that curve, or more concisely I want to control the angle and velocity at which the arrow will hit the bullseye. A diagram of the arrows motion is posted below.
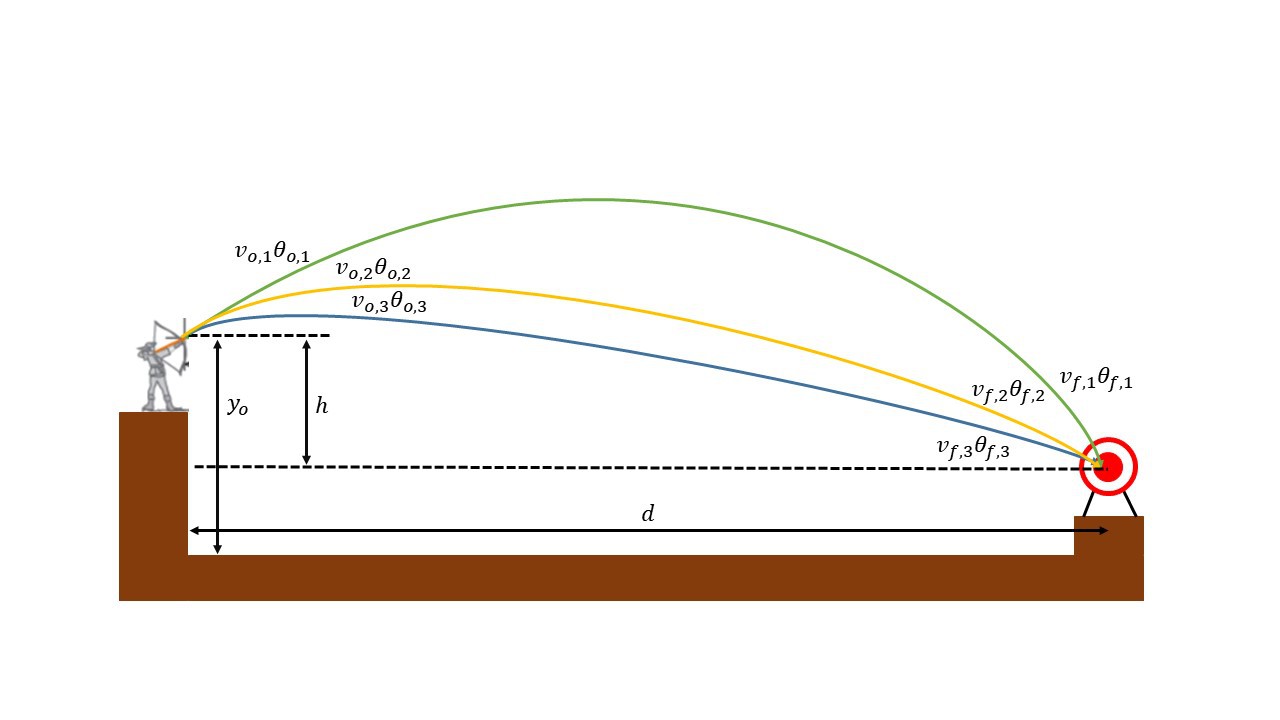
We know the depth and the height of the target using the camera as previously discussed before. There are multiple solutions for the initial angle and initial velocity if we don't care about the final angle and final velocity of the arrow. To make the solution space smaller I just set my initial velocity to the farthest the bow can extend, and solve for the desired angle, from the formula below.
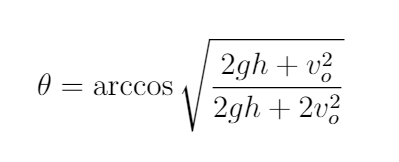
The derivation for this formula can be found after deriving the range of a projectile.
After all that high school math and physics we have a working archery robot that never misses, or at least mostly never misses.


 Piotr Sokólski
Piotr Sokólski
 SiliconSloth
SiliconSloth

Most people are facing this type of problem. further you can see my Blog: https://archerypick.com