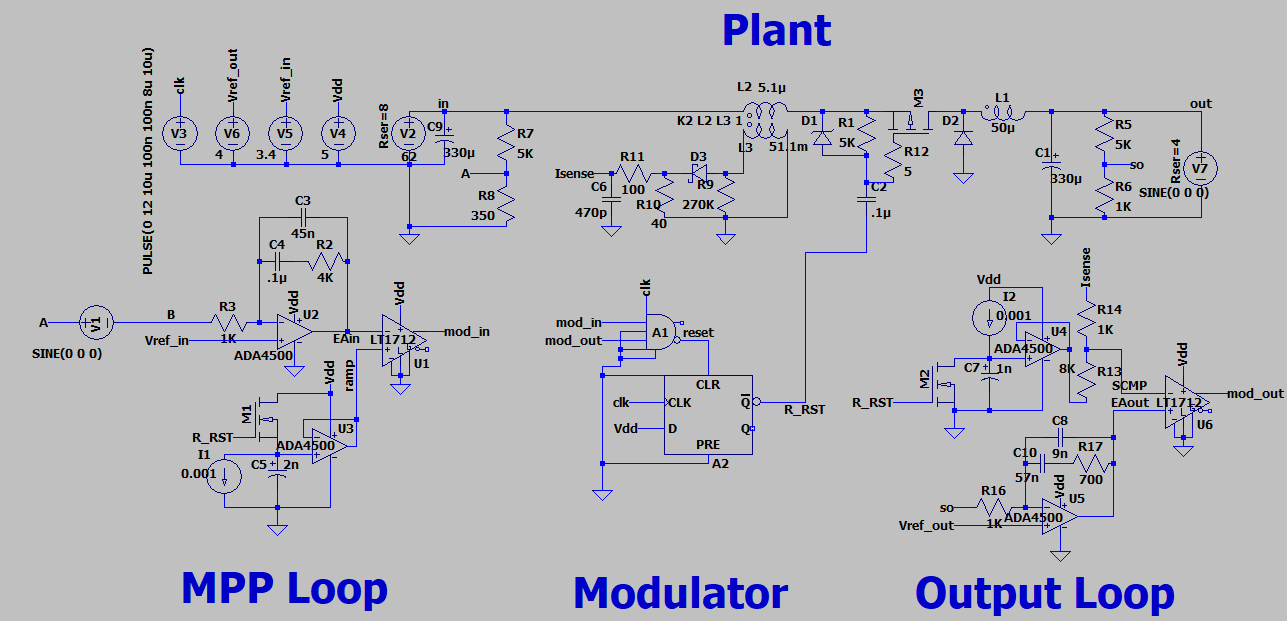
Operation
U1 is an inverting controller that biases PNP transistor Q1 acting as a shunt across V3 (note the large value of C1 in the feedback loop: fast transient response is not necessary). V3 emulates the PV panel using a series resistance to deliver the expected current at the MPP voltage for the selected panel at MPP. V2 is set to the MPP voltage for the panel. In dark or low-light conditions the panel voltage will be less than Vref and EAout will be at Vcc (or whatever the + limit is for the selected op amp). Once the panel's output exceeds Vref, U1's output will decrease to bias Q1 and maintain Vref across V3 (e.g. Vload).
EAout can then be used to limit the maximum duty cycle of the DC converter to match its impedance to that of the PV array. The specifics of how this is done depend on the controller. With a Microchip PIC (or similar) the PRG, comparator, and COG peripherals can do this. The PRG is configured for a (-) slope ramp (same as slope comp) with its output driving one input of a comparator; the other input connected to the EAout signal. When the ramp equals EAout the comparator generates a falling event to the COG for duty cycle. The PRG's rate (V/uS) is adjusted to match the converter's switching frequency and MPP curve of the array. Another possibility would be augmenting the output of a VCO that drives a variable frequency converter.
The transfer function is:
(Vref - Q1_Vbe) - (Q1_I / Q1_h_fe) * R3 = EAout
Q1_I represents the current thru Q1's emitter (or sourced from V3) and is an analog for the light energy imparted to the PV panel. Instability shouldn't be a problem since the combination of C1 and R3 keeps the gain below unity for anything greater than a few hundred hertz.
R3 should be set to ensure U1's output (EAout) can swing over the necessary voltage range needed to control duty cycle. At a minimum, it must be able to bias Q1 at MPP to maintain Vref with some margin. R3's starting value can be approximated by rearranging the transfer function:
((EAout - (Vref - Q1_Vbe)) / -(Q1_I / Q1_h_fe) = R3
Q1_I should be set slightly higher than MPP current. Also note the dependency on Q1's gain (h_fe): the data sheet's minimum value should be used.
Validation
The circuit was prototyped using TI's OPA197 on an SOIC-8 breakout. Q1 is an old MPSA56, and the PV is Anysolar's SM141K07L monocrystaline PV (its values were used for the LTSpice simulation).

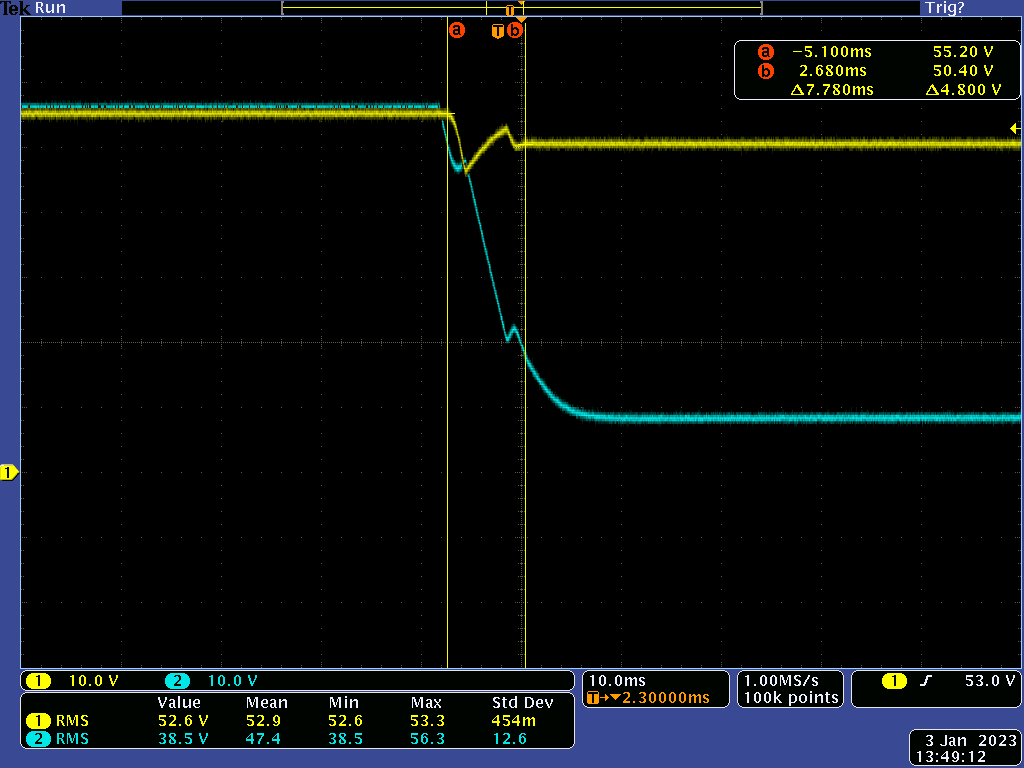
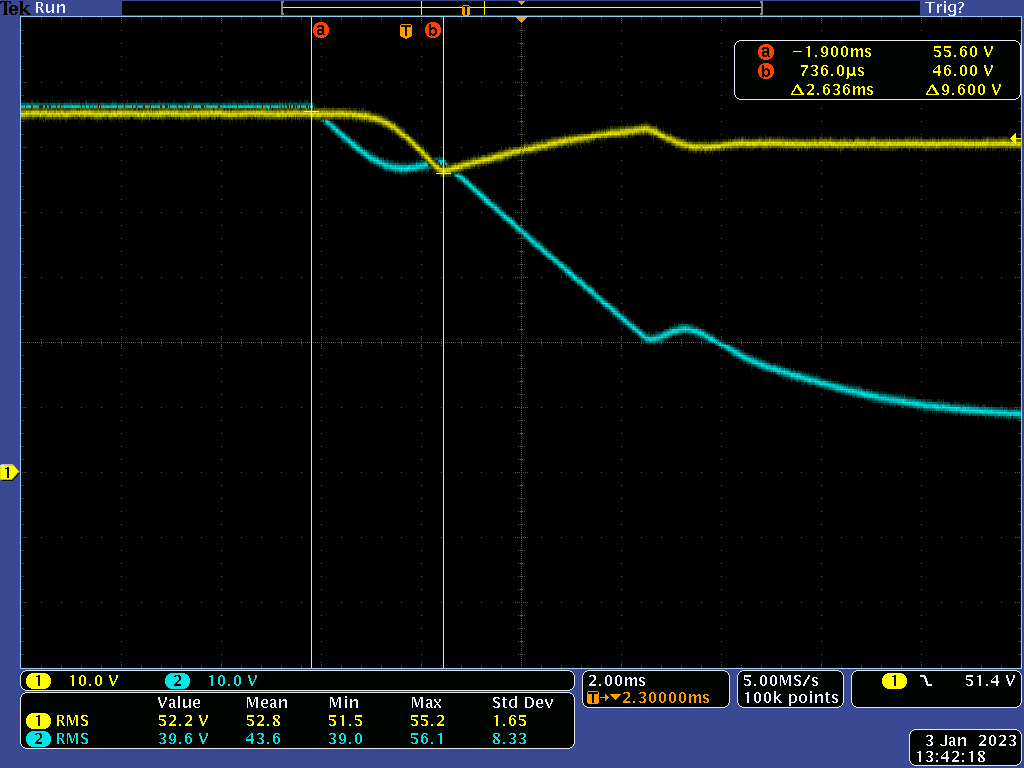
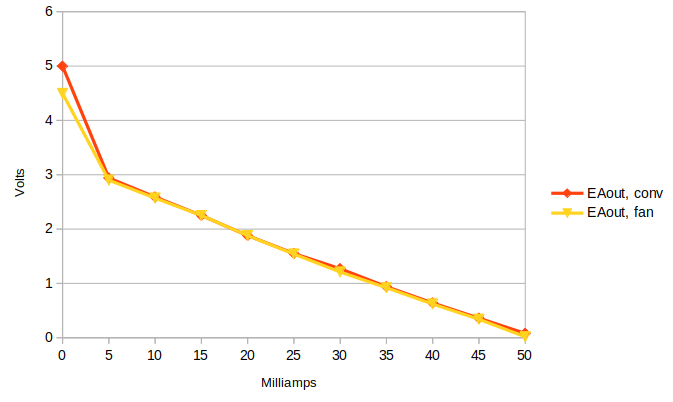
To more precisely measure EAout against the panel's output current the bench setup pictured below was used.

A VARIAC controls an incandescent bulb mounted in a box lined with aluminum foil that is focused on the panel. A cooling fan was used to provide more uniform measurements since PV panels derate at high temperatures. Below is a plot of EAout vs. PV current with & without cooling. They are nearly identical and, aside from zero output, are fairly linear.
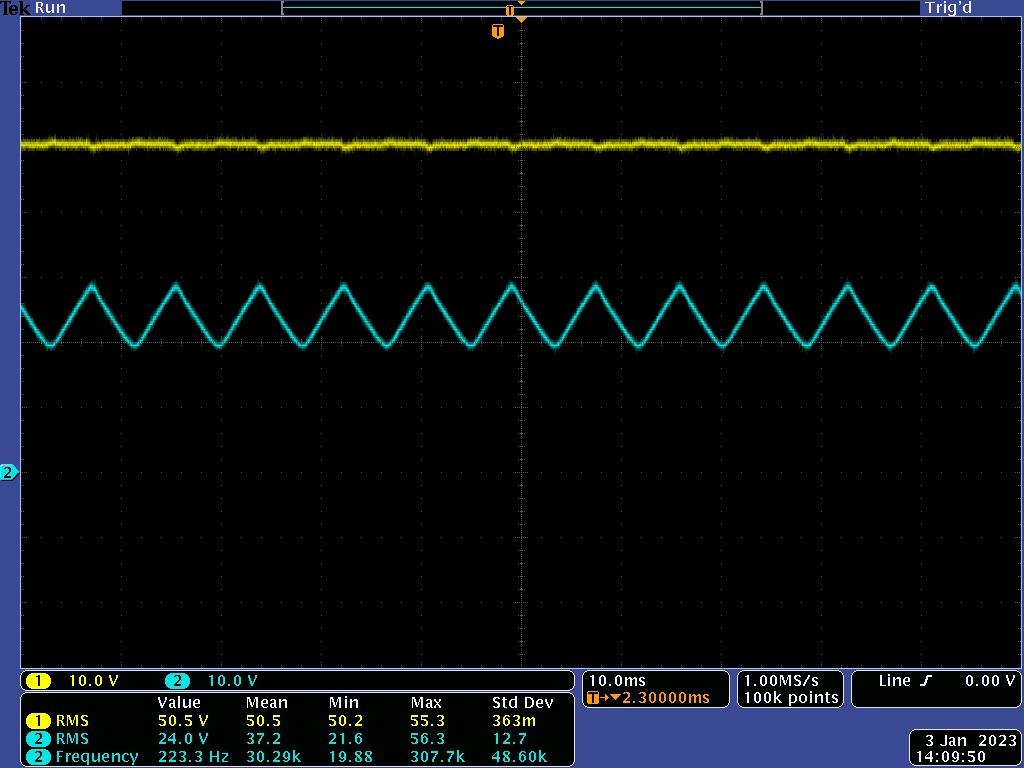
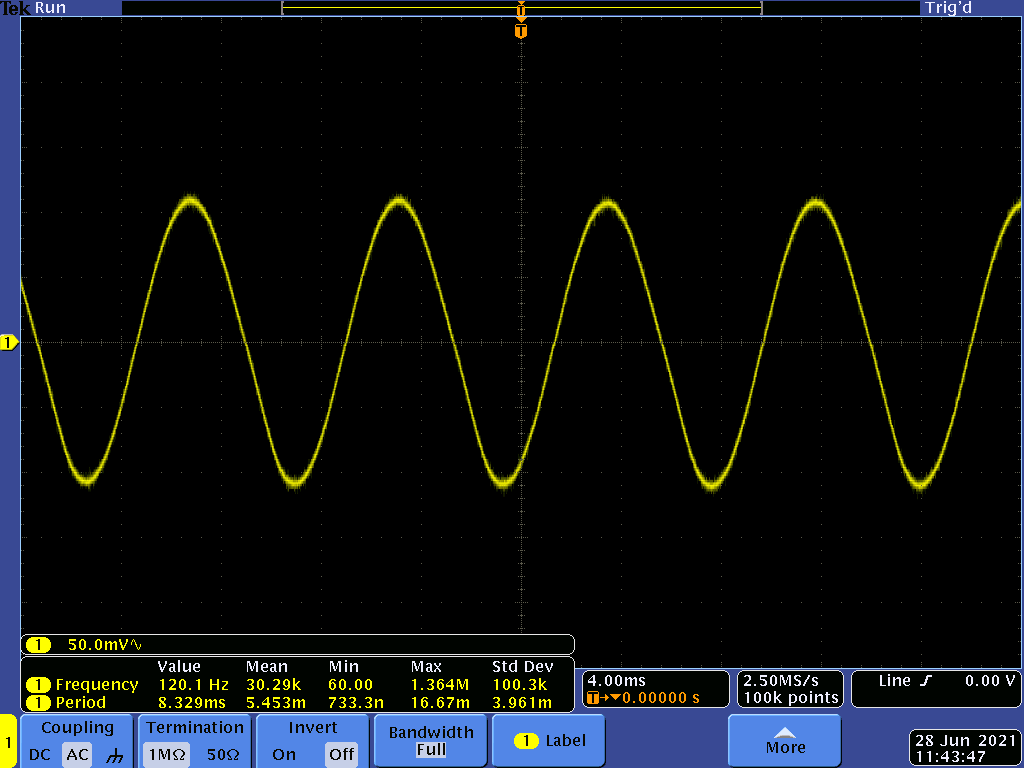
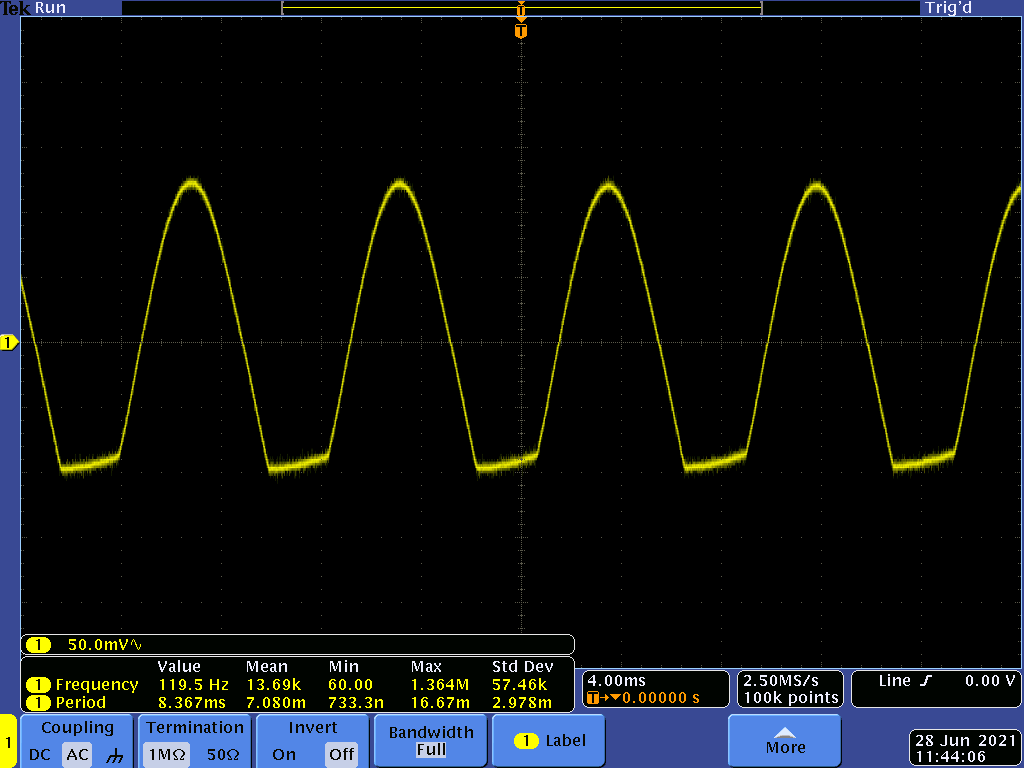
The two traces below show the OPA197's output. The first during a moderate load (~30mA) and the second approaching MPP. The negative output is clipping because R3's value is too high for the MPSA56' gain (minimum of 100 versus 200 for the 2SAR552P used in LTSpice). They are 120Hz sine waves because the bulb is powered from a 60Hz AC power source.
Implementation
This has not been tested with a working array and there are a number of considerations.
- The tracking panel must be affixed to the array and requires additional wiring back to the controller / DC converter. DCR of the run length could affect operation. Noise pickup may require shielded cable and/or additional filtering.
- This design will not work with installations subject to partial shading; the tracking PV must always be exposed to the same lighting conditions as the panels it represents.
- The tracking PV's performance curve must match that of the array as closely as possible. This includes panel type [mono]poly-crystaline, temperature, and power coefficients.
- This design functions as an open...