The joke on Hackaday is: why use a microprocessor when you can use a 555? I'm proud to announce there are times when even a 555 is too much!
Musical notes increase in frequency exponentially. Every octave is a doubling of frequency. But the keyboard increases resistance linearly for each key pressed, and the VCO oscillator outputs a frequency that's linearly proportional to an input voltage. For example, It's easy to design a system that will output 10, then 20, then 30, then 40 Hz. It's a lot trickier to design a system that outputs 10, 20, 40, 80 Hz.
Most synthesizers use the exponential gain of BJT transistors to turn a linear voltage into an exponential voltage. But this requires matched resistors, thermal compensation, and circuit by circuit tuning. There are many things that have to accounted for, or else the notes will sound too close or too far apart.
Other cheap synthesizer keyboards use 555 timers and rely on the exponential discharge of an resistor and capacitor to get an exponential output. But 555 timers cost much more than an op amp, and it's hard to find ones that run at low voltage. So, I found a way to combine two op amps and a few resistors in such a way that a linear increase in resistance from the keyboard turns into an almost exponential voltage that the oscillator can use. Technically the response is polynomial not exponential, but the polynomial is within a fraction of a percent of a true exponential.
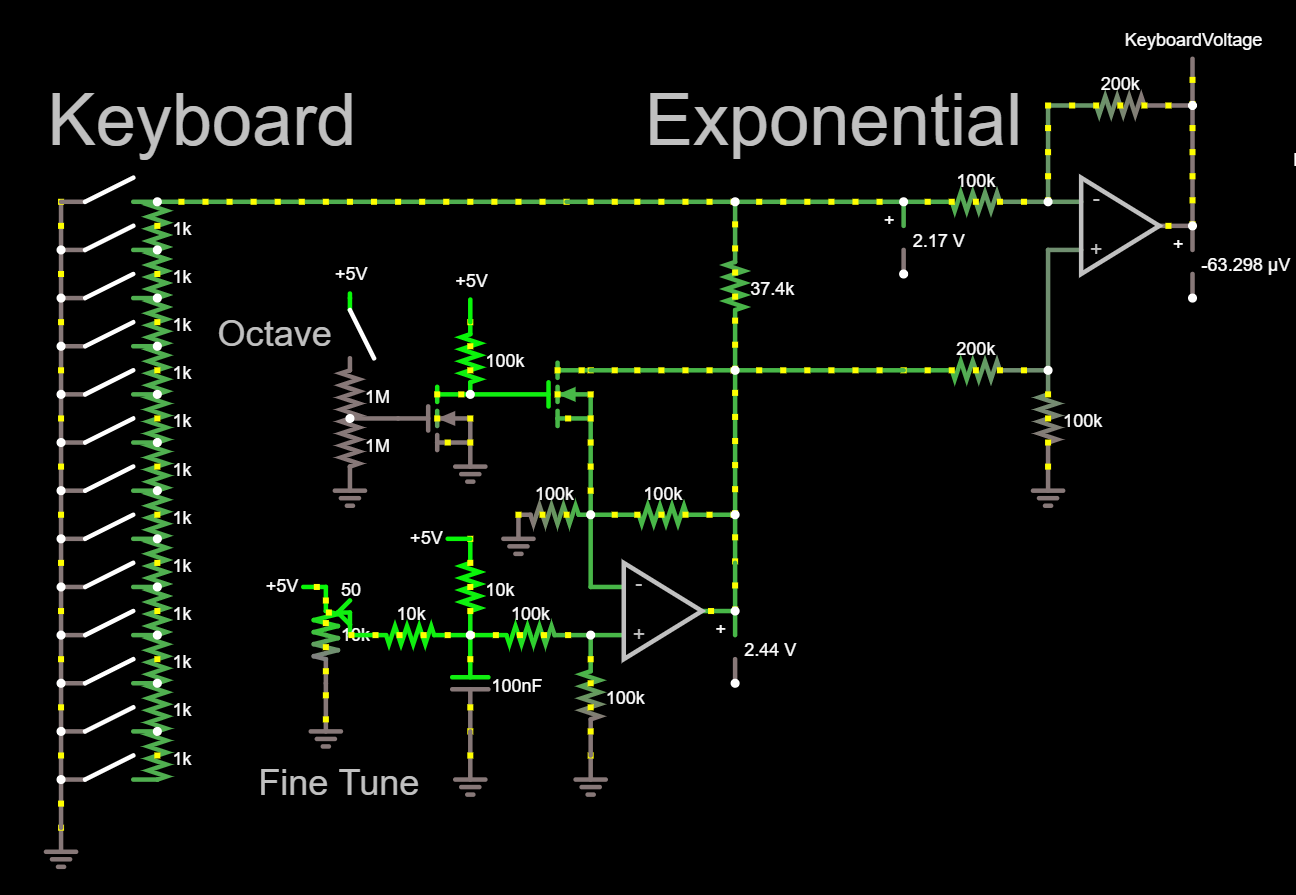
Keyboard: As discussed in a previous log, the keyboard is a series of transistors to ground, simulated here as a switch. Depending on which key is pressed, the keyboard will connect a different amount of resistance to ground. Each 1K ohm increment is one semitone (up one black or white key), with less resistance corresponding to higher pitch. If multiple keys are pressed, the highest pitch key will dominate, as all the lower keys will be shorted out.
Fine Tune: A potentiometer can adjust the voltage going into the op amp near where it says "Fine Tune". This voltage is used to shift the pitch of the whole keyboard.
Octave: The output of the fine tuning opamp can be either buffered with a gain of x1, or doubled. When the octave switch is unpressed, the op amp is configured as a unity gain buffer. But if the octave switch is closed, the op amp acts as a non inverting amplifier with a gain of 2. With one button, we can double the tuning pitch, which doubles the output frequency, giving us an octave.
Exponential: Now for the real math! The op amp that creates the exponential voltage for a linear change in resistance has no components that act exponential. How can this be? Consider the node between the keyboard and the exponential opamp. This node sees: 1) A resistor to ground that is a multiple of 1K, from the Keyboard. 2) A 37.4K ohm resistor to the tuner voltage. 3) a 100K ohm resistance to the virtual node of the exponential op amp. Because of the way the noninverting side of this opamp is set up, the virtual node will always be 1/3 the voltage of tuner voltage.
Finally, the op amp will double the voltage at this node, with reference to 1/3 the tuner voltage.
It's a ton of math! But also something any third level EE student can figure out. So if you've read this far, I encourage you to grind through the math to see what results you get. Here's what I got, from excel:
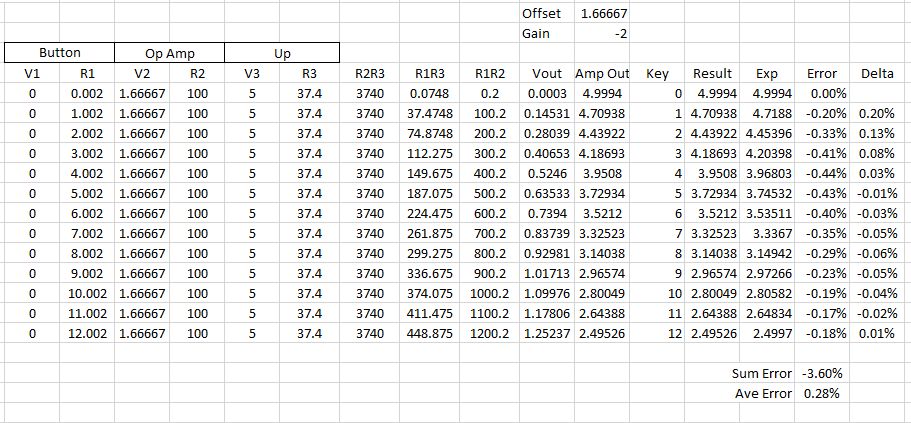
Each row shows the output voltage from a different key pressed, and compares it to an ideal exponential output. On average, the output voltage will be off by a fraction of a percent. This is less than the error we would get from the tolerance in our resistors. Anything within a percent or so is great for a toy synthesizer.
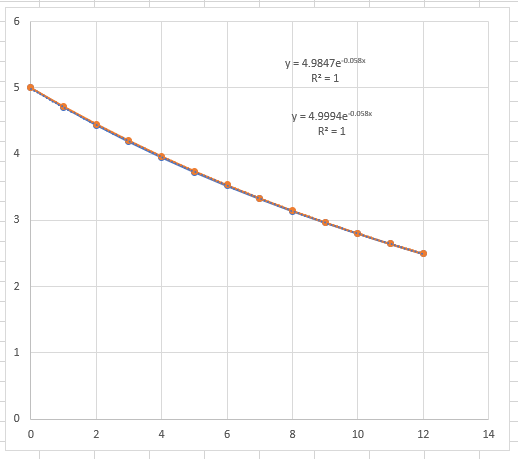
As you can see from the graph comparing the calculated opamp output to an exponential output... They are the same line. By carefully selecting components, We've found a polynomial equation that pretty much perfectly lines up with our desired exponential output. We're using standard easy to source parts (a 37.4K ohm resistor is a bit rarer but still a standard value). And best of all, we don't have to worry about thermal compensation or part to part variation, like we would if we were using BJT transistors.
And this output is scaled relative to the reference voltage. If you change the octave or the tuner voltage, the exponential curve will be scaled. But the proportional rate that voltage changes per key will stay the same, and the note spacing will stay the same.
Connect this exponential output to a linear VCO tuned to play notes in the range of musical notes, and you have yourself a simple keyboard! But it is only simple because of all the design and calculations we put into it.
 David Levi
David Levi
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.