-
Mathboard Version 1 pre-release
03/23/2024 at 15:58 • 0 commentsThe Mathboard has a new look!
![]()
Since the previous update more than one year ago, I have been working on a fully custom design for the Mathboard. The prototype Mathboard was simply an off-the-shelf 4x4 macropad, which served me well for evaluating the feasability of the project, and for developing the firmware on hardware that I could be confident in.
Once the prototype was finished and I was confident that what I wanted to build was feasible, I got started on a custom design, the result of which you see above. It has a fully custom PCB and a 3D-printed case. In the spirit of open source hardware, all the design files are available on the project github and the Mathboard can be made with a minimum of tools.
The PCB
The Mathboard uses a custom PCB that I designed in KiCAD and had produced with a rapid PCB prototype manufacturer. Keyboard PCBs are typically simple things, and this is no exception. Just a bunch of key switches, diodes, a status LED, a small 3-way switch, and pin headers for the microcontroller. In the image below you see the bottom of the PCB with the microcontroller already mounted. The microcontroller is Helios, an RP2040 board from 0xCB. I went for this particular microcontroller because of its size, cost, and large flash memory.
![]()
The Case
The case was designed in Fusion 360 and reiterated upon a few times until I arrived at a result I was happy with. The case consists of a bottom part and a lid. The Gateron V2 low profile key switches snaps into place and ensures they are perfectly aligned when soldering them to the PCB.
![]()
A small white LED diffuser can be seen in the bottom right corner in the above image. This was simply 3D printed with white PLA and glued onto the blue case with cyanoacrylate glue (aka "super glue").
-
Keycap durability test
01/17/2023 at 13:39 • 0 commentsI investigated the durability of the UV-printed keycaps of the Mathboard. The results were surprising.
I wanted to know if UV printing is a feasible method for creating the custom keycaps for the Mathboard. The process works well, but I did not know if the prints are durable. It would be a shame if the keycaps lose their decals from normal use.
I placed four Mathboard keycaps on my regular keyboard. I spaced them out evenly so that they would get roughly the same amount of use:
![]()
After only one week of normal use, the colored keycaps had nearly completely lost their decals. The white keycaps were in perfect condition.
![]()
I think this an interesting result. If anyone knows why UV prints applied to the keycaps made from colored plastic seems to adhere worse, let me know. For now, it tells me that UV printing is not feasible for the colored keycaps, but that it appears to work very well on the white keycaps. Even after months of daily use, they are looking like just came out of the printer.
-
Keycaps!
09/25/2022 at 19:22 • 1 commentI received the custom keycaps for the Mathboard today. They were made using a UV printer by a German maker I met at Nantes Maker Campus 2022. He has been kind enough to help me out with getting my design onto the keycaps.
The result looks pretty good!
![]()
If you have a UV printer and want to make these keycaps yourself, the .svg files are available at the Mathboard Github repository:
https://github.com/nup002/Mathboard/tree/main/hardware/keycaps/decals
-
Going open source
08/22/2022 at 08:54 • 0 commentsIn the spirit of open source, I have set up a Github repository for the Mathboard. Here you will find the source code, prebuilt firmware binaries, and keycap decals.
Hope it may be useful to someone!
-
Deciding on the layout
08/01/2022 at 19:24 • 0 commentsThe apparently simple task of deciding which symbols go where on the math keyboard has been more challenging than I had anticipated.
The main problem is lack of real-estate. Consider that the keyboard only has 16 buttons, while Wikipedia lists hundreds of mathematical Unicode symbols:
![]()
Clearly, it will not be possible to fit every mathematical symbol on the math keyboard. We have two ways of approaching this problem:
- Fit more than one symbol on each button
- Focus on the most-used symbols
The second solution is a bit more tricky because it requires us to make a decision about which symbols common enough to be granted a spot on the math keyboard.
Fitting several symbols per button
This approach is easy. Everyone is already used to the concept of keyboard buttons having more than one symbol. Just look at the number row, for example. They all have numbers and symbols on each button.
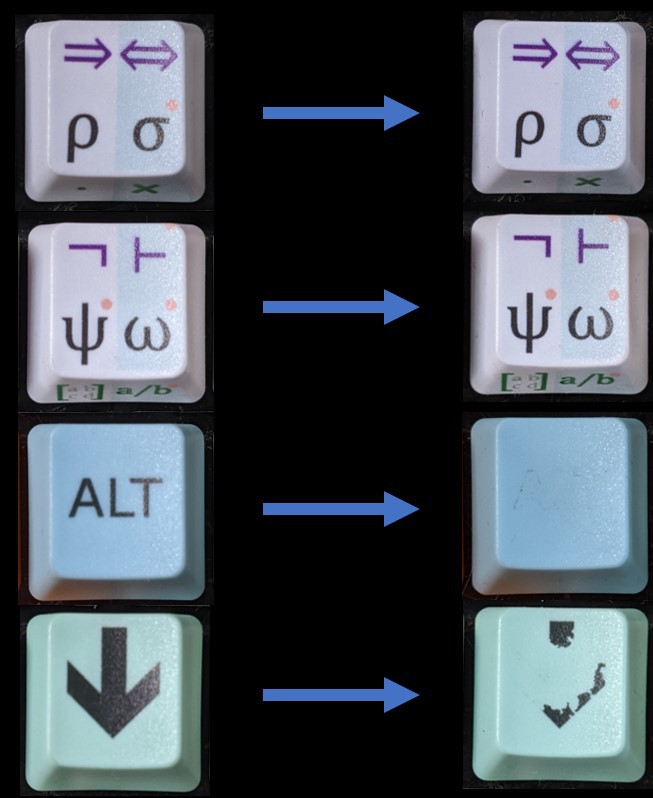
For the mathematical keyboard, I decided to fit 6 symbols per button. This may sound like it will get confusing very quickly, but I think it'll work fine. I take advtantage of the fact that the keycaps have a sloped front so one can see symbols printed on the front face.
![A single button A single button]()
A single keycap showing the locations of the 6 symbols that it can fit. The button is separated into two columns of symbols: A blue A-column, and a cyan B-column. f you simply press the button, you get a. If you hold Shift while pressing the button, you get A. If you hold Alt while pressing the button, you get α, the front-facing symbol. The same is true for the cyan B-coloumn, which is accessed by holding down Opt. So, Opt+button gives b. Opt+Shift+button gives B. And Opt+Alt+button gives β.
Therefore, by giving up only 3 buttons for Shift, Alt, and Opt, we can fit 6 times as many symbols on the remaining 13 buttons. And by a lucky coincidence we can exactly fit the 26 greek letters by placing two on each button! Perfect.
We can push this approach even further by allowing certain symbols to have multiple different versions accessible by double-tapping, triple-tapping, or even quadruble-tapping the same button. This is useful for certain symbols like roots (√, ∛, ∜) and integrals (∫, ∬, ∭). It can also be used to negate symbols (∈∉, ∃∄), or to access uppercase-versions of letters (δΔ, θΘ, σΣ).
Selecting the most commonly used symbols
This part has been difficult. The goal of the math keyboard is to be as useful as possible to as many people as possible, which means that the symbols that go on the keyboard must be the most commonly used ones. But what is a "common" symbol? I decided to refer to Wikipedia on this matter, with their excellent Glossary of Mathematical Symbols.
From this article and based on my own experience, I decided on the following groups of symbols (with a few examples in paranthesis):
- Greek letters (α, β, γ)
- Comparisons and equivalence (≠, ≈, ≪)
- Algebra and calculus (∑, ∫, √)
- Set theory (⋂, ∈, ⊂)
- Logic (⇔, ∃, ¬)
- Diacritics and supscripts (◌̂, ◌̃, ◌⁰)
- Various others (⋅, ±, ∞)
These groups should hopefully cover most of what a regular mathematician, phycisist, or engineer will need. It is of course likely that many users will miss a few special symbols that they need often, but this is unavoidable.
The layout
I eventually decided on the following layout:
![]()
Each key is separated into a light 2x2 top face and a dark 2x1 front face. Each key also has a green main section and blue Alt section.
The symbols with a red triangle in corner has additional symbols accessible by multi-tapping the key. Double-tapping greek letters gives their uppercase versions if they differ from the Latin alphabet. So double-tapping σ will give you Σ, but double tapping α does nothing since that would just give you an A.
Double tapping the set theory symbols will negate them. For example, double tapping ∈ gives you ∉.
For all other symbols, multitapping will access additional versions of the same symbol. For example, double tapping ≪ gives you ⋘. Double tapping ◌₀ gives ₁, triple tapping gives ₂, and so forth.
-
Motivation
07/05/2022 at 10:18 • 0 commentsThis log entry relates to the motivation behind creating the mathematical keyboard.
When you want to type mathematical equations on a computer, you have a set of options.
- Type it in LaTeX
- Type it in the Microsoft Office or Apache Open Office equations editor
- Type it in plaintext for simple equations like α ≤ β ± 2 °C
The TL;DR is:
- LaTeX is really flexible but requires practice and memorization of codes
- Equation editors are flexible but requires a lot of clicking around in menus
- Plaintext requires copypasting from a source for each symbol
In each case, the mathematical keyboard will save the user time by reducing the amount of memorization, clicking, or copypasting, by simply having the codes, symbols, and operators available with a single keystroke.
Typing in LaTeX
Of the three, typing in LaTeX is the most flexible and has long been the standard in many scientific fields like mathematics and physics. The downside to LaTeX is that it requires you to memorize LaTeX codes. Often these codes are logical, like `\alpha` to get α, or `\plusminus` to get ±. Other times they can be a bit more obscure, like `\ngtr` for ≯ . And when you get into limits, sup/subscripts, and advanced formatting it quickly gets messy. Let's look at what's needed to type the Fourier Transform definition:
The LaTeX code for this equation looks as follows:
\hat{f}(\xi) = \int_{-\infty}^{\infty} f(x)\ e^{-i 2\pi \xi x}\,dx,\quad \forall\ \xi \in \mathbb RIf you have never written equations in LaTeX this can seem daunting. Many new users of LaTeX spend a good chunk of their time looking up the codes for the symbols they need, and how to make sure they appear in the way they want them to. You'll usually see undergraduate and graduate students alike with LaTeX cheat sheets covering the walls of their study area. A keyboard that automatically writes the correct codes for commonly used symbols and operators might save them some time.
Typing in an equations editor
Typing in the Microsoft Office or Apache Open Office equations editor has the benefit of much of the same flexibility as LaTeX, but with the need for copious amount of clicking around in menus. Typing the Fourier Transform definition in the Word equations editor took me 46 mouse clicks in 5 different menus, and that's the best case after some practice. All this time spent clicking around and looking for the correct symbols in different menus could be reduced by the mathematical keyboard.
Typing in plaintext
The Unicode standard defines a large set of mathematical symbols, and it is therefore possible to type simple equations alongside the regular text. This is very useful when you just want to, for example, remind the reader that σ = ±2.2 or that ε ∈ ℂ . You can even define slightly more advanced equations, but there is a limit due to the lack of Unicode support for superscript, subscript, and much more. But if we try to write the Fourier Transform in plaintext we get:
f̂(ξ) = ∫_(-∞)^∞ f(x)e^(-i2πξx) dx, ∀ ξ∈R
Doesn't look too great, but it works. The downside to typing in plaintext is that almost none of the symbols are available to you on a typical keyboard layout. When did you last see a keyboard with an integral sign on it? You will either need to copypaste every symbol from a source like Wikipedia, or memorize their 4-character Unicodes. For example, typing in Alt+222B gives you ∫. But this also requires you have a keyboard with a numpad, which isn't that common anymore. A mathematical keyboard would be hugely useful when you want to type plaintext equations.
 Magne Lauritzen
Magne Lauritzen