Modern computers offer gigabytes of RAM and more processor cores than we have fingers to type with. But as we all know, a hacker isn’t defined by the tools at their disposal, but rather the skill and imagination with which they wield them.
So this year, we’ve taken a slightly different approach. Rather than try and cram the badge with even more state of the art hardware than we did in 2019, we’ve decided to go back to the well. The 2022 Supercon badge is a lesson in what it means to truly control a piece of hardware, to know what each bit of memory is doing, and why.
Make no mistake, it’s going to be a challenge. In fact, we’d wager most of the people who get their hands on the badge come November 4th will have never worked on anything quite like it before. Folks are going to get pulled out of their comfort zones, but of course, that’s the whole idea.
We have an extensive tutorial for you below. Start here!
Tools, including the assembler, emulator, and a bunch of example code can be found in the Supercon6 Badge Tools Github repo. (Pull requests welcome!)
There's an online assembler as well!
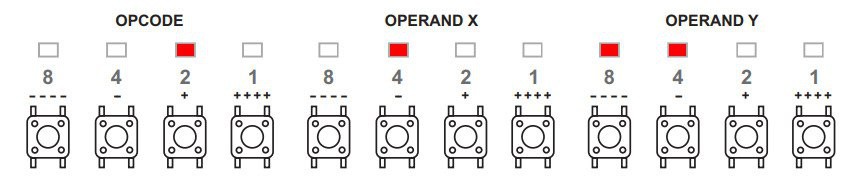
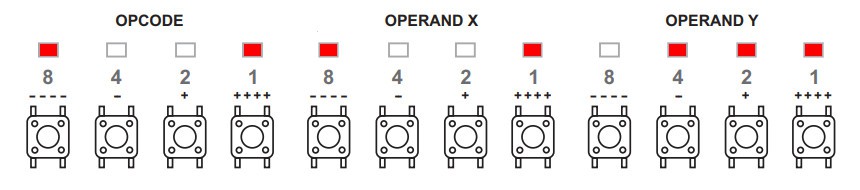
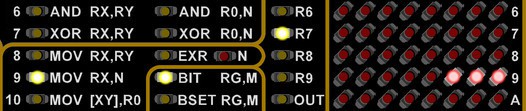
And if you want to know absolutely everything about the badge, you will find it in Voja's extensive documentation PDF, found here: Official Badge Page - Technical Deep Dive
 Lutetium
Lutetium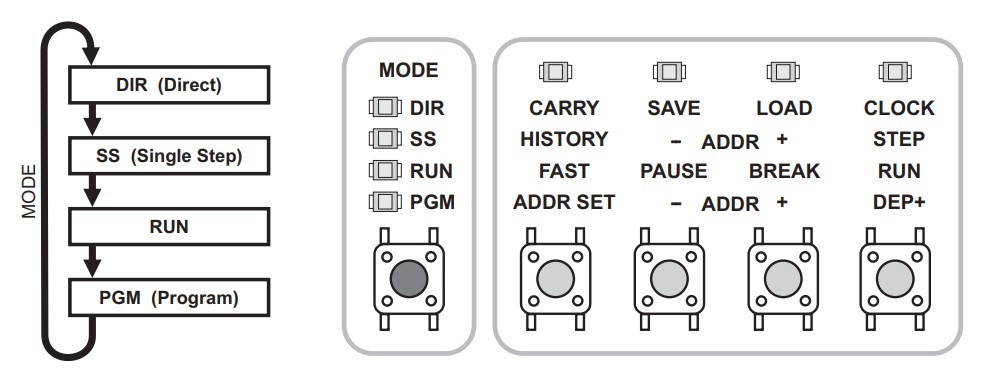












 Tindie
Tindie
 xres0nance
xres0nance
 Zapp
Zapp
Here is the first version of an assembler/code synthesizer I wrote for the badge: https://github.com/adrianfreed/Supercon6BadgeWork