I think I've tweaked the component values into something possibly usable. The feedback resistor seems to improve the speed tremendously - by keeping the transistors out of saturation - at the cost of greatly reduced gain. But maybe we don't need that much gain? Here are the latest component values:

the feedback resistor is new. It keeps the voltage on either base away from the rails to prevent either transistor saturating. An unfortunate side effect of this arrangement is a greatly reduced gain - at DC, the gain is approximately the ratio of the two resistors 2.2k / 1.6k = 1.375. Yes, this is very small - I thought it would be too small to be useful, but maybe it's OK, if you're careful. To get a feel for just how small this is, here's the voltage transfer function, which would normally be a sharp step function for an inverter:

For most of the input voltage range, this is a linear amplifier. It's only at the extremes that it starts to look like a logic gate. But, since the output stage is symmetrical and low-impedance, and the input stage high-impedance, maybe this is enough gain to build logic circuits. Theoretically, you only need a gain of 1 after any losses...
Then again, consider the speedup capacitor. At 10 MHz, that 100 pF capacitor has an impedance of about 160 ohms, so the gain is now around 14. That doesn't sound so bad.
I built an early hardware test (with different RC values) of a ring of inverters with feedback resistors. At 1.1V supply, they were happy to just sit there and bias themselves to 1/2 the supply without oscillating - the gain was too low. At 1.2V, they always started ringing, and once started, they kept going as the supply was turned down to about 0.7V. So, I started simulating things at 1.2V instead of 1.1. The final supply voltage will probably need a tuning knob.
Speed Simulations
The original problem from a few logs back was that the logic worked well with high-speed square waves, but not at low or high duty cycles. I'm convinced now that rapid switching was keeping the pair out of saturation. A short pulse after a sustained high or low input wasn't enough to pull one of the pair out of saturation. The added feedback resistor holds the base voltage close to the midpoint, keeping both transistors out of saturation. This allows the gate to respond to brief, isolated pulses as well as waveforms with high repetition rates. Here's a test waveform at the input and output of a chain of 10 inverters:

The measured delay for 10 inverters is around 16 ns, or 1.6 ns per inverter. This is significantly faster than what I had seen before. I haven't constructed any of these inverters yet, so I can't be sure it will work with real components. The initial low period above is a test for the saturation problem. Without the feedback resistor the PNP saturates on the initial stretch, and we get this - no output at all:

I suspect the output would eventually start switching because this is only a 5 MHz square wave, but I didn't let the simulation run that long.
Fan-out Test
In this simulation, the second-to-last stage drives a fan-out of 10 inverters.

This slows down the trailing edge of the first pulse so that it happens at a 31 ns delay (instead of 16 ns with the simple inverter chain). With a fan-out of 5, the delay is 24 (as opposed to 16) - so maybe a rough rule of thumb is that fan-out is roughly equivalent to cascading stages. It looks like driving 2 inputs delays the signal about as much as chaining 2 inverters. If the delays were all due to RC effects, this would be the case. This is not great, but might be acceptable. Again, I haven't measured this on the hardware yet.
In any case, increasing fan-out decreases switching speeds. You see this with CMOS logic where the input capacitance of added driven inputs slows down the transition speeds. Although with integrated CMOS families, the effect is not this pronounced.
Input/Output Impedance
I roughly estimated the output impedance of the stage at 9 ohms. The input impedance is above 1.6k until about 350 kHz, then drops to about 200 ohms at 10 MHz. The vertical axis is labeled in volts because I used an AC current source to probe the input impedance.

I won't paste plots here, but these gates drive 50 or 100-ohm terminated lines just fine. I tested outputs with split-terminations of 100 ohms to ground and V+ (for 50 ohm lines) and 200 ohms to each (for 100 ohm lines). No problems at all, which is what you'd expect from under 10 ohms output impedance. With fast edge rates, you might have to use terminated lines to maintain signal integrity. Of course, you can also source-terminate transmission lines, but you can't fan-out and source terminate (unless your transmission lines are exactly the same length). I didn't look at how many split-terminated loads you can drive - but at least (2) 100-ohm loads, since you can drive (1) 50-ohm load.
NAND Gate
These component values translate straightforwardly into the NAND design:

In simulation, the upper input shows a delay of about 2.3 ns, and the lower input shows about 3.6 ns. It may be possible to balance these somewhat by tweaking the component values a little, but I haven't had a chance to try yet. Like the inverter, the NAND has no problem with saturating during long periods of stationary input values; the feedback resistor has cured the mysterious square-wave illness.
Next Steps
I need to build some of these gates from actual components and see if they perform as well as the virtual ones. The low DC gain of these stages troubles me a little, but I think the logic is still workable.
UPDATE 20170121 : How much gain is actually required?
I was a little hesitant at first about the low gain of these gates. Then I started thinking about the minimum gain that would be required to meet commercial CMOS family specs. Here's what a worst-case (lowest gain) transfer curve would look like that still meets the Vih, Vil, Voh, and Vol specs from a datasheet:
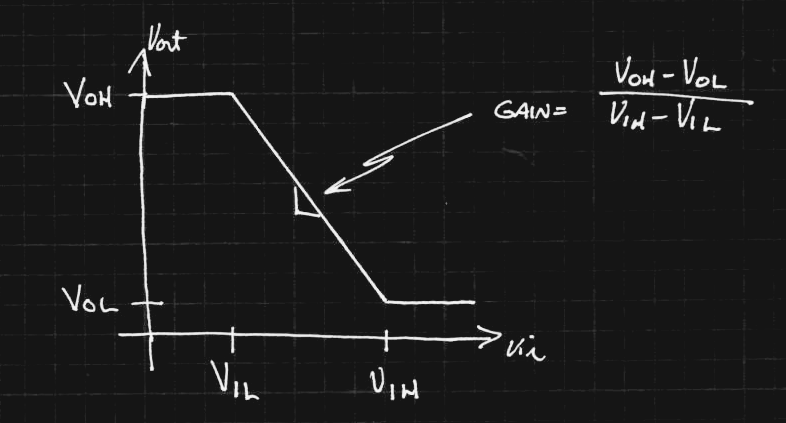
For the 74HC04 at 6V supply and with all worst-case values, we get (5.2 - .4)/(4.2-1.8) = 2.0. At a 2V supply, it's (1.9-0.1)/(1.5-0.5) = 1.8. Hmm, maybe 1.375 isn't that crazy after all.
 Ted Yapo
Ted Yapo
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
@Ted Yapo you made another mind-blowing log !
Are you sure? yes | no
I ran a bunch of simulations with different topologies, nothing as sophisticated as SPICE, so very questionable if they were realistic. I did see the slow-response effect with the old design... It seemed to be some combination of the input capacitor and the capacitance across B-E. Actually, it still seems to exist with feedback, but definitely less noticeable. One interesting thing about this simulator is that it shows the current-flow animated along the wires. The output appears to toggle when the input crosses 0.6V.
Hey! When you edit a comment, you can actually modify the link!
Are you sure? yes | no
The link looks funny, but clicks OK, and I can see/play with the circuit. That's an interesting simulator. I wonder what is underneath doing the calculations? Could it be SPICE? Is there a FORTRAN-to-javascript translator?
Are you sure? yes | no
I have no idea what the underlying system is for that simulator. My experience with SPICE is 15 years in the past, but *as I recall* you set up a simulation, then run it, and get "answers" at the end... can't change the circuit, resistor-values, etc. mid-simulation to see the effect, or watch waveforms as it performs the calculations... Essentially, you have to know what you're looking for and won't see things you don't look for. (E.G. with the simulator, showing the current-flow in one circuit I tested, I noticed that there's actually current *leaving* the base of an NPN-transistor... certainly wouldn't've expected to look for that!)
But, I could be entirely mistaken about SPICE, like I said, it was a LONG time ago.
Are you sure? yes | no
ugh, this is the first time I've ever considered using one of those url shorteners... if I knew which ones were trustworthy, I'd definitely use one for this.
Interesting thing, it seems like the current flows through the capacitor almost exclusively.
Are you sure? yes | no
The 100pF capacitor has 1.6k of impedance at 1 MHz (1/2*pi*f*C), so at any frequency above that, it carries more current than the 1.6k resistor.
Are you sure? yes | no
That simulation makes me want to create alligator clip leads with LEDs built in that chase at a speed proportional the the current through the wire. You could make that thing in real life.
Are you sure? yes | no
haha, nice.
Reminds me of the first time I saw EL wire, they used it in a model train-set to show the power-lines...
Are you sure? yes | no
And... Since the output-voltage is still rail-to-rail, inserting the feedback resistor essentially ties the input at the bases through a resistor to a virtual-ground halfway between the two rails, no? The effect being to reduce the overall voltage-swing at the bases around a center-point, roughly 1/2 V+...?
Are you sure? yes | no
I think you might achieve similar non-saturation results with a "pull-sideways" resistor to mid-supply, but that would have other different effects. For one, it wouldn't linearize the response (no negative feedback), which may actually be a good thing to eliminate. Also, the feedback increases the input impedance (like with an op amp).
@Yann Guidon / YGDES mentioned using such a resistor somewhere. It's probably worth a try.
Are you sure? yes | no
Yep I remember thinking that, you came up with the more practical feedback trick. But I've recently "ancient" circuits (50's, 60's) using bias to different, non-power-supply rails.
Are you sure? yes | no
Then there's this from the front page of the project, and the back page of the paper you found about direct-coupled logic:
Those Rb's look like they're there to prevent the transistors from saturating. Since the input is driven with split resistors, you can split the saturation-prevention R, too.
People have been through this exercise before.
Are you sure? yes | no
indeed, they have. "There's nothing new under the sun" so they say...
Didn't realize that was in the same paper... I barely read it, to be honest, since I was dead-set on finding circuits with PNP-emitters tied to ground (that weren't using negative power-supplies, unlike the extremely confusing drawings from the part of that paper I was reading).
Looks like you're well on your way to recreating the work in that image.
Some more experiments here
Good luck finding a power-supply that has *exactly* the voltage of *exactly* the VBE-ons, summed ;)
Are you sure? yes | no
It's funny what we can (re)discover when we take the time to read our elders...
I feel vindicated in my weird, crazy, ridiculous, expensive projects just from all I learned from them ! They make a much better professional :-)
Are you sure? yes | no
@Yann Guidon / YGDES, indeed, about learning from the past. It's interesting to learn different methods, and as you said makes for better/more-informed designs...
One thing I did catch from that paper was a discussion about their rationale for disregarding other BJT-based logic-topologies. One justification--from a time when "integrated circuits" had something like a dozen transistors, and integrated-circuit-logic was in its infancy--was that adding transistors to silicon was an expensive process, so they tried to minimize the number by using single-transistor inverters, like an NPN with a pull-up resistor.
Imagine if thoughts and limitations like those directed the development of BJT-based integrated-circuit logic... And, yet, with the now-ubiquitous CMOS, we're using two transistors per inverter. The number-of-transistors limitation has basically been eliminated. And, interestingly, a larger limitation today is that resistors can occupy more silicon than a transistor.
Could lead one to wonder if there are topologies, plausibly CBJT, that went undiscovered, dismissed, or otherwise lost to yesterday's limitations, that could actually prove to be useful today.
And, even if it doesn't, it's a great learning experience.
Are you sure? yes | no
So, do I understand correctly, the 50% duty-cycle "biasing" (from before the feedback resistor) had to do with [bias] voltages stored in internal capacitances?
Are you sure? yes | no
I don't know - your guess is as good as (probably better than) mine. I don't fully understand why it happens - other than a vague thought that the DC component was acting as the bias. The DC component of a 50% wave is right at mid supply, keeping the devices out of saturation. It deserves some more thought and experiment.
Are you sure? yes | no