Loop Filters
I have been working my way through the loop filter types, so far:
- Low Pass
- 1st order PID
- Passive Lead-Lag
- Active Lead-Lag
No problem with the first three:
Low Pass
PID
Lead-Lag
The Active Lead Lag Filter
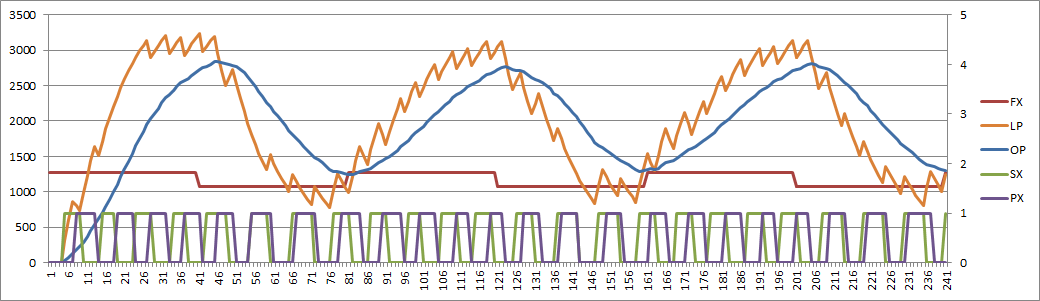
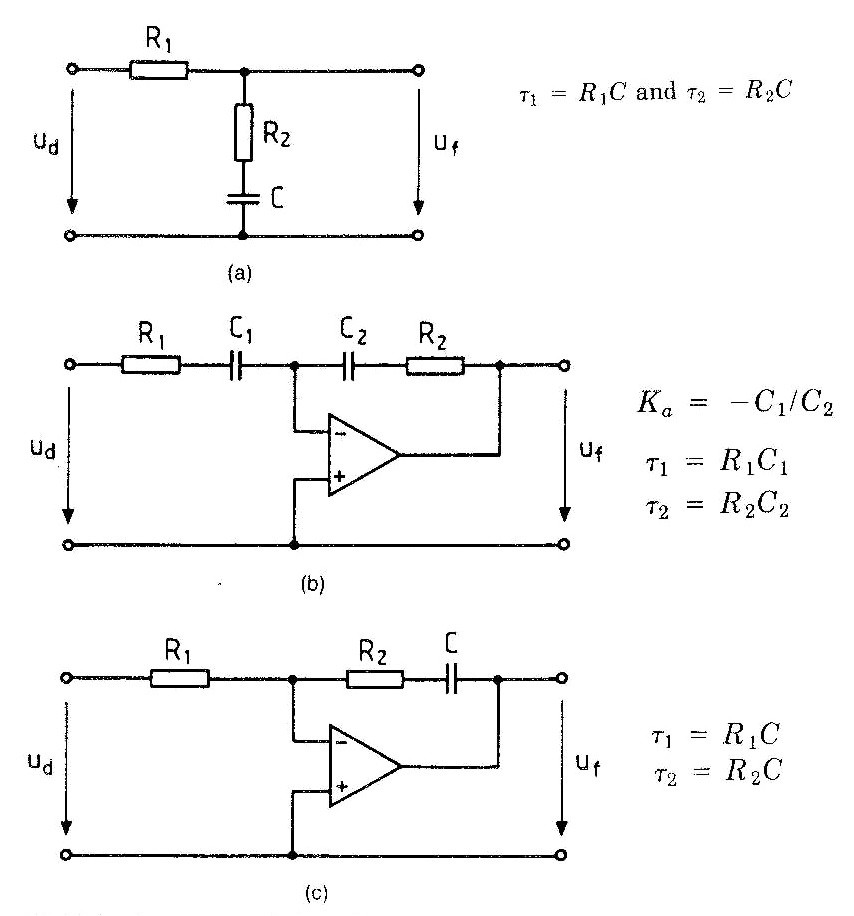
Here are the analog domain basic loop filters. The problem filter is shown at the bottom of the image:

(source: http://www.globalspec.com/reference/38390/203279/2-6-second-order-phase-locked-loops)
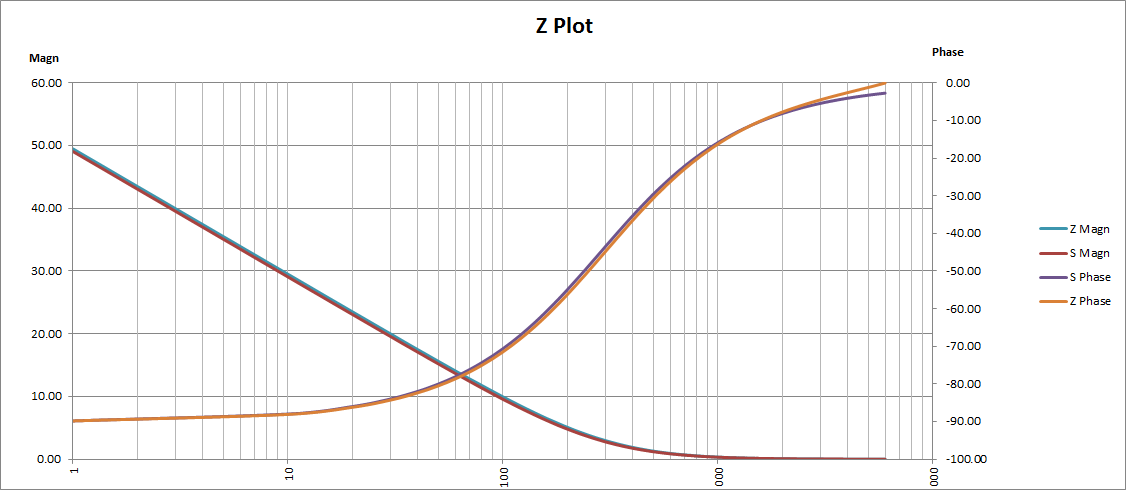
I have plotted the S domain versus the the modelled Z domain and the Z domain is good up until about Nyquist, so no problems:
- LP0 = (69 * PD0 + 10 * PD1 - 59 * PD2 - 0 * LP1 + 64 * LP2) \ 64
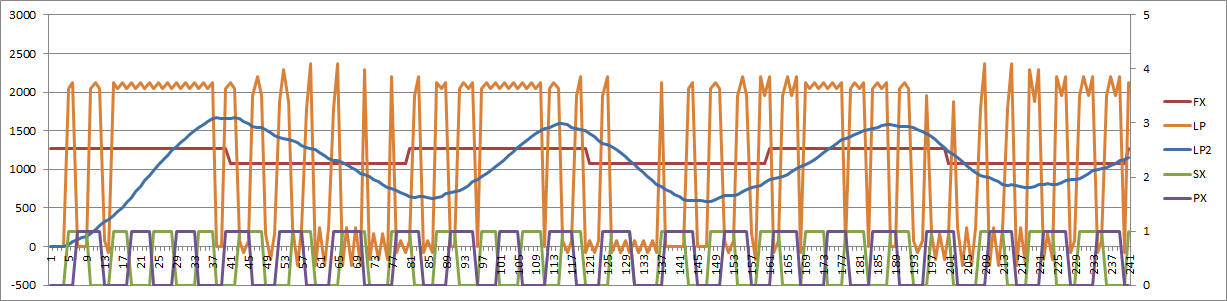
The issue is that this filter cannot be used directly. The DC gain is +46dB and as the structure is that of an integrator and the PD is 0 to K, the filter just blows up:
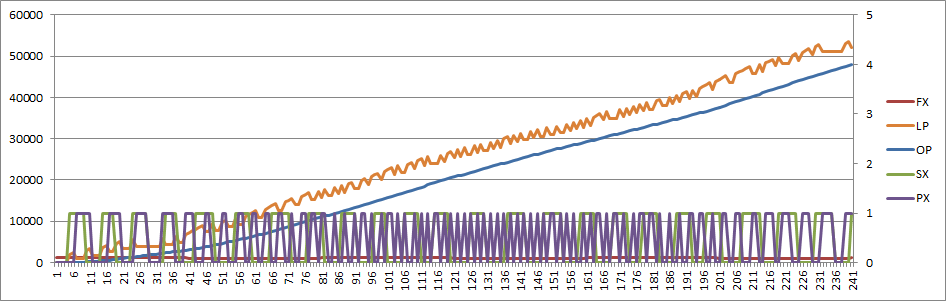
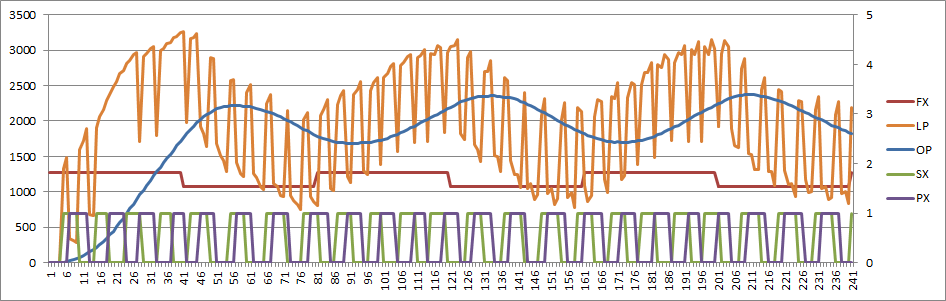
After substituting the PD for a differential PD (i.e. -K/2 to +K/2) I get something that basically works:
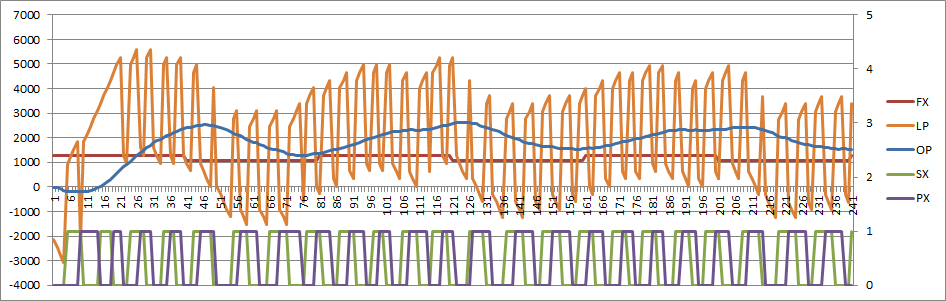
(Note that the vertical scale has changed compared to the other PLL filters)
The analog equivalent is:| K | 4000 | =KpKv | |
| R1 | 5600 | R | |
| R2 | 5600 | R | |
| C | 0.000000100 | F | |
| T1 | 0.00056 | ||
| T2 | 0.00056 | ||
| WN | 2673 | =sqrt(K/T1) | |
| D | 0.75 | =T2/2*sqrt(K/T1) |
The main advantage of the last filter is greater range of control of damping factor and natural frequency.
Choosing a Loop Filter (The Shoot Off)
Now that I have all the filters working which one to use going forward? Active Lead-Lag or PID?
Active Lead-Lag Loop
Inputs:
- K (KpKv)
- R1
- R2
- C
Intermediate:
- T1 (=R1C)
- T2 (=R2C)
- WN (=sqrt(K/T1))
- D (=T2/2*sqrt(K/T1))
Code (after calculating Z-transform coefficients):
- PD2 = PD1
- PD1 = PD0
- PD0 = PD * K - K \ 2
- LP2 = LP1
- LP1 = LP0
- LP0 = (B0 * PD0 + B1 * PD1 + B2 * PD2 - A1 * LP1 - A2 * LP2) \ D
- LP = LP0
PID Loop (First Order)
Inputs:
- WN (natural frequency)
- D (damping factor)
- SR (sample rate)
Intermediate:
- T1 = 1 / WN / WN
- T2 = 2 * D / WN
Output:
- Kp = Proportional factor
- Kp = (1 + 1 / Tan(1 / (2 * T2 * SR))) / (2 * T1 * SR)
- Kp ~ (1 + 2 * T2 * SR) / (2 * T1 * SR)
- Ki = Integral factor
- Ki = 1 / (T1 * SR)
Code:
- PD1 = PD0
- PD0 = PD
- LP = Kp * PD0 + (Ki + Kp) * PD1 - LP
Conclusion (The Shoot Off Results)
It looks rather like a "no-brainer" to go with PID from a computational point of view (all other things appearing to be equal). Funny how the common wisdom of PID in the discrete domain is confirmed!
AlanX
 agp.cooper
agp.cooper
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.