Shading
Before I can make this model look real I have to do a bit of work regarding how the light falls on it, and it gets a bit complicated because the real one is curved, and the virtual one is made of plane surfaces.
Calculating the path of a beam of light (RayTracing) as it bounces off a surface isnt easy, you need to know the angle of the beam of light, and the angle of the surface, both in 3D. This has to be done after the model is posed for the render, so the only way to know the surface angles for sure is to know their original angles, and back-track the gimballing in the same manner as the leg is calculated.
What, for every pixel? I dont think so... That sounds like hard work. Lets think about it a different way then.
Cloud Theory to the rescue (again)
The model is represented as a cloud of atoms with planar surfaces, tiny squares. Each and every one of them has a unique position and angle of incidence, which is calculable, to give the visible area of the model.
I use IsFacing ( <coords > ) to tell me whether to draw these polygons, because it calculates the area covered by the polygon. If it is negative, it is back-to-front. However, it just returns true or false. If you look at the actual area returned, it is a percentage of its full area when facing the camera directly. When it is sideways-on, it has an area of zero, no matter which way it is facing, left-right or up-down.
This means, by finding the difference between the drawn area and the original, I can tell how much it is facing me without knowing its actual angle, and shade it accordingly.
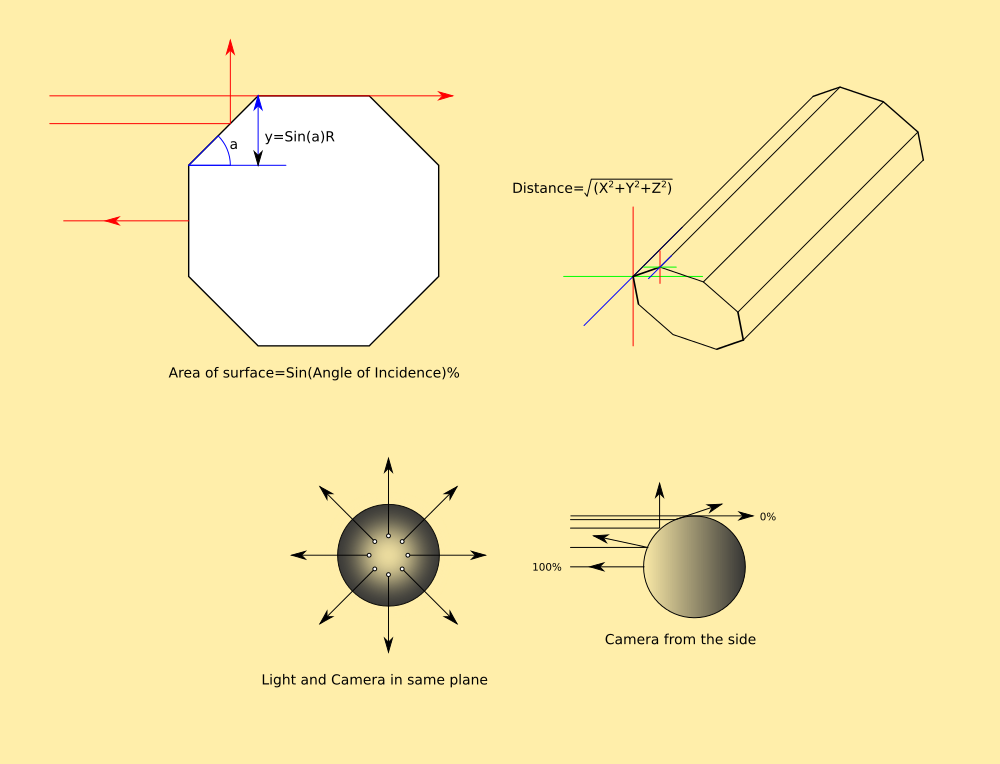
All polygons facing have 100% area, all polygons side-on have 0% area, and all polygons with -100% area are facing away. This makes it very simple to resolve the shading from the camera, and then rotate the scene to show the shading from another angle.
Because it is a rotation, the area and angle are related together by the Sine of the angle. The full area can be calculated by finding the lengths of the sides in 3D, as X,Y,Z offsets as two triangles.
The Law of Cosines could then be applied to give the angles of the sides, and it could be drawn flat without knowing what angle it is facing in any plane...
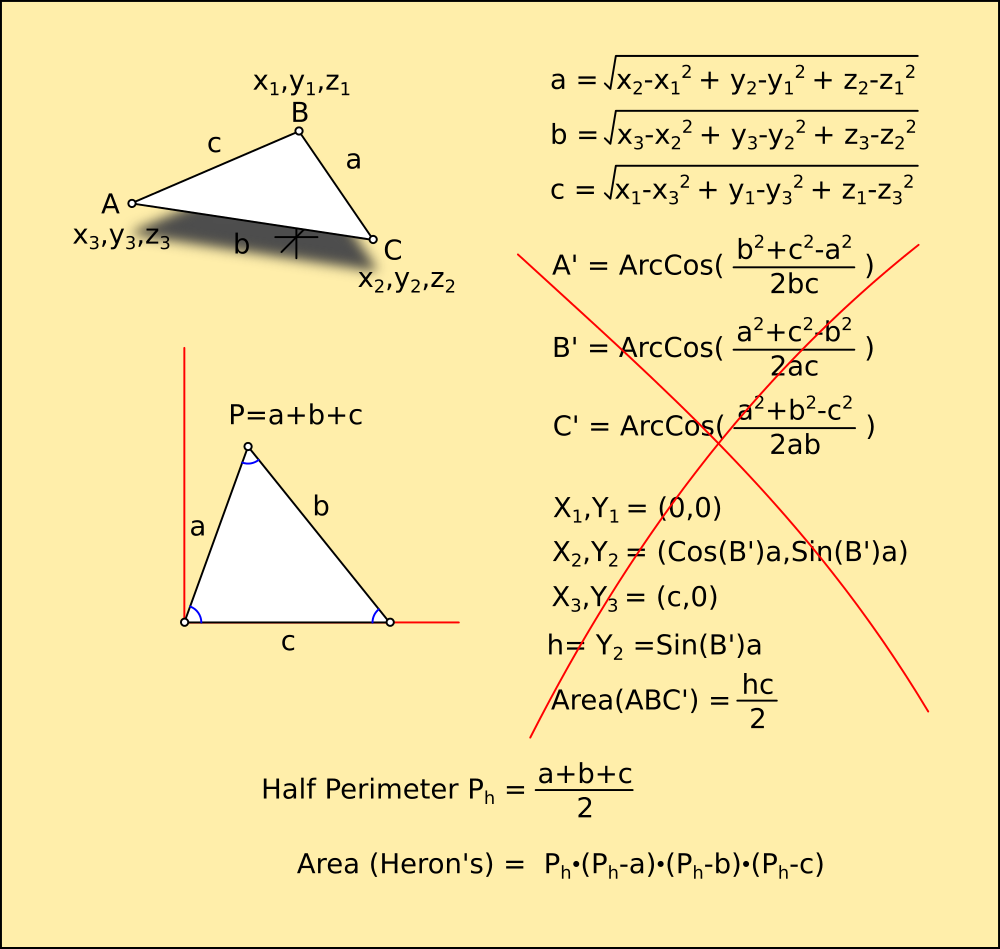
However, after a bit of digging through my research I realised you can find the area of a triangle much more simply if you know the sides without calculating any angles. Heron's Formula uses the perimeter and ratios of the sides forming it, much nicer. I'd forgotten about that one, usually you wont know all three sides without work so its just as quick to find the height.
Once it is drawn flat, the area can be calculated as two Euclidean triangles, and the Cartesian Area subtracted from it to give the angle of incidence as a tangent.
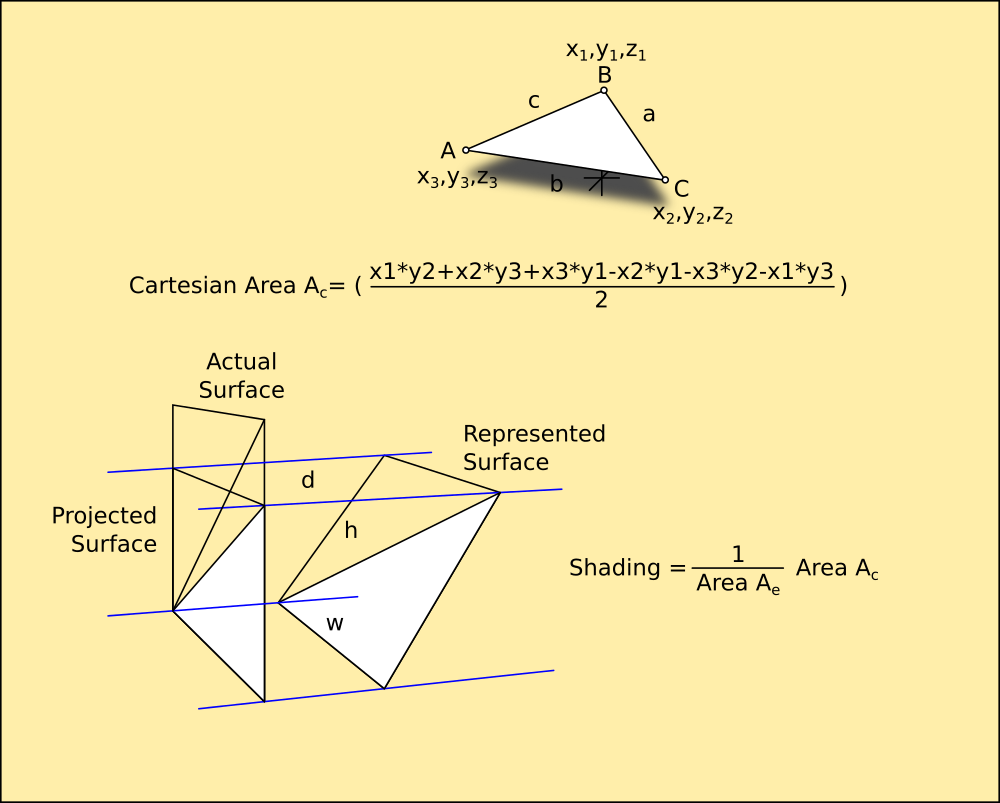
The resulting figure is a real value between 0 and 1, giving the amount of atoms visible as a percentage. Because each atom has no height dimension, any atom viewed from the side is not visible, and also covers any atoms behind it so they are no longer visible. This means a 10x10 atom square viewed from the side has an area of 10 atoms; its length or width, because all you can see are the leading 10 atoms on the edge. Viewed from directly facing, it has 100 atoms visible. And at 45 degrees only half of each atom shows behind the atom in front, making the area half.
This means I can calculate how much light falls on any pixel without knowing the angle of the surface it is in, just by calculating how much of it shows. Because I also dont need to know the angle of the light-rays either (they are parallel to the camera axis and therefore zero) I can do this after posing the model, using the information embedded in it as an abstract.
Because each polygon is a rectangle its very easy to graduate the shading across the surface so it appears smoothly curved in two directions instead of planar.
def cartesianarea(crd):
for n in range(len(crd)-1): # remove duplicate coordinates
if len(crd)>n:
if crd.count(crd[n])>=2: crd.remove(crd[n])
if len(crd)==3: # if there's 3 left
x1,y1,z=crd[0] # pick 1st 3 points
x2,y2,z=crd[1]
x3,y3,z=crd[2]
area=x1*y2+x2*y3+x3*y1-x2*y1-x3*y2-x1*y3 # find triangular area, if its negative its facing down
return area/2.0 # return the area
else: return 0 # otherwise its not a polygon
def euclideanarea(crd):
global d2r
for n in range(len(crd)-1): # remove duplicate coordinates
if len(crd)>n:
if crd.count(crd[n])>=2: crd.remove(crd[n])
if len(crd)==3: # if there's 3 left
x1,y1,z1=crd[0] # pick 1st 3 points
x2,y2,z2=crd[1]
x3,y3,z3=crd[2]
a=sqr(((x2-x1)*(x2-x1))+((y2-y1)*(y2-y1))+((z2-z1)*(z2-z1))) # find the lengths
b=sqr(((x3-x2)*(x3-x2))+((y3-y2)*(y3-y2))+((z3-z2)*(z3-z2)))
c=sqr(((x1-x3)*(x1-x3))+((y1-y3)*(y1-y3))+((z1-z3)*(z1-z3)))
p=(a+b+c)/2.0 # find the perimeter and halve it
return sqr(p*(p-a)*(p-b)*(p-c)) # return area by herons formula
else: return 0 # otherwise its not a triangle
These work nicely...
c=[[-10,-10,0],[10,-10,0],[-10,10,0]] # make a triangle around 0,0,0
for a in range(0,360,45): # step through 360 degrees every 45
d=[] # make a container
for x,y,z in c: # go through the coords in c
d.append(rotate(x,y,z,'x'+str(a))) # rotate them by a and put them in d
print 'angle: '+str(a)+' cartesian area: '+str(cartesianarea(d))+' euclidean area: '+str(euclideanarea(d)) # show the results
angle: 0 cartesian area: 200.0 euclidean area: 200.0
angle: 45 cartesian area: 141.421356237 euclidean area: 200.0
angle: 90 cartesian area: 3.67394039744e-14 euclidean area: 200.0
angle: 135 cartesian area: -141.421356237 euclidean area: 200.0
angle: 180 cartesian area: -200.0 euclidean area: 200.0
angle: 225 cartesian area: -141.421356237 euclidean area: 200.0
angle: 270 cartesian area: -6.12323399574e-14 euclidean area: 200.0
angle: 315 cartesian area: 141.421356237 euclidean area: 200.0
>>>
Rotating triangle c around (0,0,0) always returns its correct area with EuclideanArea, and a ratio of it with CartesianArea, which is negative when facing away.
All I need do is
(1/EuclidianArea)*CartesianArea
to bring it into the range -1 to 1, with 1 describing the triangle facing towards and -1 facing away.
 Morning.Star
Morning.Star
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.