We have been talking about differential calculus- the study of how something is changing. There’s another half, though – called integral calculus. Loosely speaking, integral calculus is the process of reversing what you do with differential calculus. You can start with a derivative, and figure out what the original curve was. Think of it like addition and subtraction being inverses of each other. It’s just a little bit more complicated here.
As you can see in the picture here, Joan had to party like it was 1979 with her old MIT Calculus 1 book to be sure what we're saying here is right... note the heavily-used eraser, which is always a key tool in algebraic calculus.

Integrals
let's look at what an integral is. Most simply, in two dimensions it is a way of figuring out the area under a curve. Suppose we wanted to find the area under the curve from 1 to 2 on the horizontal axis. At point 1, the curve has the value A. At point 2, it is B. As 1 and 2 get closer together, a line drawn along the curve approximates the line more and more closely.
Suppose we wanted to find the area under the curve between the two vertical arrows marked A and B. If the red line was EXACTLY the curve, then the area would be C times the average of A and B. As the distance C gets smaller and smaller, the red line gets closer and closer to being the same as the curve. We could use a rectangle of height equal to the average of heights A and B to get the same area as finding the area under the triangle plus rectangle we'd need to figure out otherwise. You can see the diagram of this from Newton's own copy of Principia.
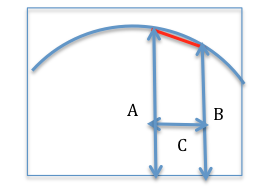
Suppose we also drew a line parallel to the red line. Newton found that you can always draw a line parallel to this line which is tangent to the curve. This is called the Mean Value Theorem. We will come back to that later when we talk about tying together integral and differential calculus.
The Surface
The surface we will use as an example here is called a swallowtail catastrophe. It is a surface that has some special properties that you can look into and think about a little based on what you know already, and we will use it as an example for more things to come.
The basic swallowtail equation we used was
f(x,y) = offset + ( x^5 + a * y * x^3 + b * x^2 + c * x ) / scale
Where "x^5 " means multiply x times itself five times (or, if you prefer, raising x to the 5th power), " * " means multiply, and the height of the surface is a function of two other variables, x and y. a, b, c and d are constants, and a has to be negative. For the examples we show you here, a = -10, b = c = 1.
Depending on how many data points there were, we needed to fuss around a bit with scaling and offsets so that the values of the function were always positive, since otherwise the bottom of the model would not have been a plane.
Besides having a cool name, the swallowtail is a relationship that comes up often in nature for systems that are chaotic -- acutely sensitive to initial conditions. It was also the basis for Salvadore Dali's last painting, The Swallow's Tail. (Thanks go to our mathematician friend Niles Ritter, who did his PhD thesis on related mathematics and suggested it would be a fun surface to play around with in our endeavors. Everyone else uses a paraboloid- what fun is that?)
First we will print this as smoothly as possible. It was printed with the equation printer in Chapter 1 of our 3D Printed Science Projects book; the OpenSCAD model is CC-SA-NC and available at the pubisher's repository at the same link. The surface is shown printed just in free space, and also as a surface covering a volume.

Volumes Under Surfaces
If we can get an area under a curve, it's not surprising we can do the same thing to computer the volume under a surface. Suppose we wanted to try approximating a surface by a series of rectangular solids in three dimensions and get the volume under a surface by adding up the volume of each of these rectangles. We have demonstrated this by creating little rectangular blocks with height at the mean value for a 61x61, a 16x16, and an 8x8 grid, plus the smoothest possible version. We have 3D printed all these, as you can see in the next picture. (We will post these three STLs shortly in the FILES section.)

You can see that a 61 by 61 grid is really pretty good, other than being a little rough on the surface.
How to Print a (Flock of) Swallowtails
Finally, we printed four of these at once so that those high peaks would not be distorted by overly-short times between layers. The four surfaces (the three ones with discrete rectangles, and the continuous ones) all printed in about twelve hours on a Bukito. if you printed one at a time, you'd probably have to use a cooling tower (a sacrificial tall skinny object) to keep the blobbiness at bay.

So now we have seen that a derivative is just a tangent to a curve, and an integral is just an area (or volume, in 3D) under a curve. How do those relate? Stay tuned.....
 Joan Horvath
Joan Horvath
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
Yes, that's a great way to explain integral calculus! It's like the inverse of differential calculus, where instead of finding the change rate, we see the original function. And just like addition and subtraction are inverses of each other, differentiation and integration are inverse operations. Finding the area under a curve is one of the most common applications of integral calculus. For example, if we are given the vertices of a parallelogram, we can use integral calculus to find its area by integrating the function that defines its sides. Before meeting the experts from https://plainmath.net/integral-calculus/16043-find-the-area-of-the-parallelogram-with-vertices-a-3-0-b-1-5-c-7-4-and-d-5-1 and beginning better learning math, I was always so stressed when I had to find what is the area of the parallelogram with given vertices. It is easier when you have study support and help.
Are you sure? yes | no