-
Ye Olde Gigatron and Гигатрон
08/26/2020 at 15:09 • 0 commentsThere's two Gigatron "specials":
Ye Olde Gigatron
The Gigatron was designed to run with old TTL chips. The kits were supplied with modern, CMOS type chips, but the goal was to keep it TTL compatible. Marcel had already started sourcing some old TTL components, most notably an old 70ns SRAM. I've taken over that task, which has led to the creation of what I call "Ye Olde Gigatron". (And yes I know "Ye" was pronounced "The" and the word "Olde" does not exist.)
Not counting the clock and the 75HC595, all the ICs are old. The newest IC on there is the RAM, which is from 1991. All the rest is pre-1990, so over 30 years old!
I've thrown in a mix of stuff:
- 54LS, extended temperature range ("mil-spec")
- 74, standard TTL
- 74S, Schottky
- 74LS, Schottky low-power
Ye Olde Gigatron is a bit unstable and it consumes a whopping 1.2Amps. It requires a good power supply so I used my lab power supply. Also the clock did not work at first. The 74HCT04 provides a clock booster and that started ringing so I had to add a resistor. The clock circuit will not work with Schottky components, so I left in a 74HCT04. A 7404/74H04/.. will not work in a Pierce oscillator design. Still looking into using a 74C04.
The components used are:
6x 74163 (National Semiconductor, 1972)
4x 74157 (Stewart Wagner, 1975)
4x 74153 (Fairchild, 1976)
2x 74283 (Fairchild, 1978)
1x 74S240 (Signtics, 1979)
2x 74S153 (National Semiconductor, 1980)
2x 74S153 (Signetics, 1981)
2x 74S138 (Fairchild, 1982)
3x 54LS377 (Texas Instruments, 1982)
1x 74LS273 (Motorola, 1983)
1x 74LS244 (Signetics, 1984)
1x 74LS153 (Raytheon, 1985)
1x 74LS244 (Signetics, 1986)
1x 74LS32 (Motorola, 1986)
1x 74LS139 (Fairchild, 1986)
1x 27C1024 (ST Microelectronics, 1988)
2x 74LS273 (Texas Instruments, 1989)
1x 62256 (Micron Technology, 1991)
If somebody has older components than this, let me know :-)
2. GigatronskiSince I gave a talk about the Gigatron at Neuron hackspace in Moscow, I wanted to make a Gigatron with old Soviet chips. Unfortunately, I did not get any from my new Russian friends. By the way, Pavel and others of Neuron Hackspace have a wonderful "Flipper Zero" kickstarter project.
But anyway, after a long time occasionally looking for Soviet TTL chips, I suddenly found Evita, a company in Vilnius, Lithuania, that has a lot of NOS Soviet components. I was able to order everything there. One chip appeared to be broken, but the company send me a replacement at no extra cost.
The chips were new. The newest of the lot is manufactured in 1992 (so strictly speaking, not Soviet but Russian!). They have a different colour than the IC's I'm used to seeing. Also on quite a few, you can see a piece of aluminum on the bottom. I've opened one up, to see that this is used to put the die on before the epoxy is added.
The Soviet chips also have a different pin spacing (2.5mm instead of 2.54mm). But I was able to (gently!) get them all into their sockets, even the larger ones. I did spend quite some time looking for Soviet replacements of the 62256 SRAM and 27C1024 EPROM, but don't believe they ever existed. The 75HC595 is also not available. A Soviet 74LS04 can be found, but it will not work in the pierce oscillator (same as with Ye Olde Gigatron). There is a Societ 74ACT04 version called КФ1594ЛН1, but that is pretty rare and I could not get one. Since it's used for the clock and not the CPU itself, it is not that much of a problem.
I got a white PCB from somebody in Hong Kong, which I used for the Гигатрон. I swapped SRAM in between pictures. It now has the same old SRAM as Ye Olde Gigatron.
Since I ran out of VGA connectors, I bought a cheap one from China, instead of buying from Mouser/Farnell/Digikey, which I've always done for the kits. Although cheap, it also is not as mechanically sturdy and.. quite a bit smaller, so it no longer aligns with the serial connector. Oh well. -
The Gigatron lives on!
07/16/2020 at 14:42 • 0 commentsThe Gigatron lives on!
Dutch company Budgetronics is offering Gigatron kits. They are a bit different to what we used to ship though:
- No wooden enclosure included
- No game controller included
- No manual included (you can download & print yourself)
- Black PCB instead of green
Since there's less included, the price is also lower: € 99.95
If you attach a PS/2 keyboard, you have all the functionality, as ROMv4 is included (preprogrammed) as well as the Pluggy McPlugface PS/2 adapter.
https://www.budgetronics.eu/en/building-kits/gigatron-retrocomputer-building-kit/a-25779-20
-
Gigatron fully open source
06/11/2020 at 10:33 • 0 commentsThe Gigatron TTL computer is now fully open source! The source code had been open source (BSD license) since the beginning of course. A while ago, we published the design files for the printed circuit boards, both for the Gigatron and for Pluggy McPlugface, the PS/2 adapter.
We have now also made the full Assembly and User manual available online, under a CC-BY-SA license. The assembly manual contains the list of components, which is now also available separately as a Bill of Materials under the same license.
These files should enable to you make your own Gigatron. The only part that is no longer available is the custom made wooden enclosure.
If you decide to build your own Gigatron, we won't provide support. But we do encourage people to go down the rabbit hole :-)
-
1000! And Gigatron future
05/28/2020 at 10:47 • 0 commentsIn the last year, a lot has happened. We now have 6502 emulation and the Gigatron can run Apple-1 code, such as WozMon. We have BASIC running and there's a great BASIC compiler, opening the way to create great games. Looking back on the original goal to play tic-tac-toe on a LED matrix, we are super chuffed that we have a system running BASIC that feels like an actual homecomputer from years ago - still without a microprocessor.
And today, Gigatron #1000 has found a new owner! Thanks to everybody for making happen what we could not have dreamt of when we started!
![]() We have decided to stop selling kits once our stock has been sold, which should be in a few months. For us, the Gigatron was always about inventing new things, understanding technology, designing, fine tuning, tinkering, and also about meeting like minded people (and having fun in the process). Making it into a kit had its own charmes, writing a manual, sourcing components, designing a PCB. Packaging and sending out kits, however, resembles a plain job too much, but was needed to create a community of people that would also want to design, understand and tinker.
We have decided to stop selling kits once our stock has been sold, which should be in a few months. For us, the Gigatron was always about inventing new things, understanding technology, designing, fine tuning, tinkering, and also about meeting like minded people (and having fun in the process). Making it into a kit had its own charmes, writing a manual, sourcing components, designing a PCB. Packaging and sending out kits, however, resembles a plain job too much, but was needed to create a community of people that would also want to design, understand and tinker.That community now exists, and wonderful things have already come from it, both in hardware and software. So we will stop selling and providing support in a few months. Does that mean you can no longer get a Gigatron? No, you still can, because the PCB layout, the schematics and the software have all been open sourced. The only thing you probably cannot get is the wooden case that we had tailor made for the Gigatron. Somewhere in July or August, the assembly manual and more will open sourced as well. We hope the Gigatron will live on!
-
The gtBASIC compiler for games
05/05/2020 at 09:31 • 0 commentsThe Gigatron can be a great gaming machine. However, Tiny BASIC is a bit too slow for games and nowadays not everyone wants to do assembly. Yesterday at67 formally released his solution to this dilemma: the gtBASIC compiler(!) supporting sprites, sound effects and music! Now there's NO excuse to turn the Gigatron into the retro game console you always wanted. I hope this brings the platform to a whole new level.
![]()
![]()
![]()
-
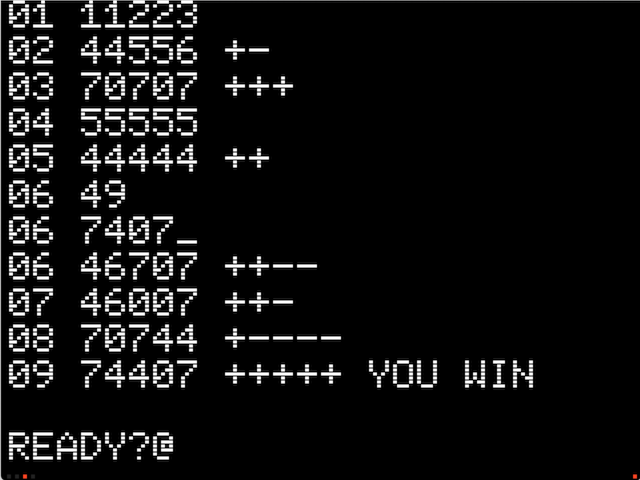
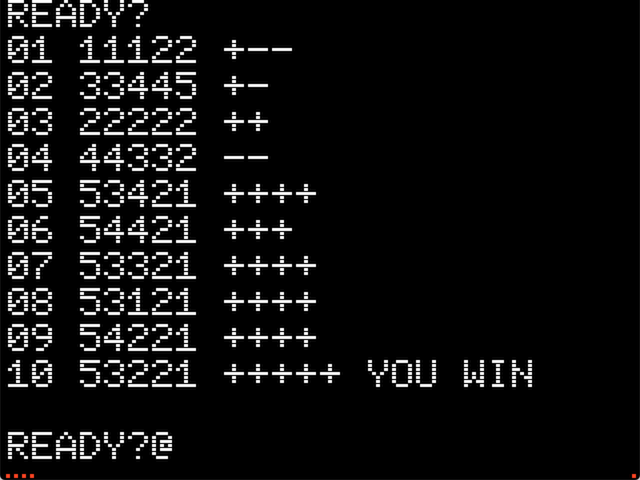
Mastermind in 177 bytes
02/22/2020 at 12:21 • 0 commentsTyped in from this 1976 Dr Dobbs article. Worked first time.
![]()
Except that we don't do decimal mode and Woz used that to increment the "tries" counter on the left side. So you better win the game in less than 10 tries (or accept a hexadecimal count).
If we sacrifice 13 more bytes, we can get the correct try count without using BCD mode:
![]()
190 bytes works for me.
-
Why settle for two BASICs when you can have four?
12/27/2019 at 20:47 • 0 commentsToday we gained two more BASICs. One new, one very old. First at67 offered his BASIC compiler for the Gigatron. This project has been brewing for over a year. It's still in alpha, but it is GREAT already. This is a cross-compiler that creates fast Gigatron binaries. This is fantastic news for those who like to write games but don't want to dive too deep into the Gigatron machine languages. This week it built our Christmas greetings, with snow physics and Jingle Bells tune.
![]()
Video link: https://streamable.com/5ds9d
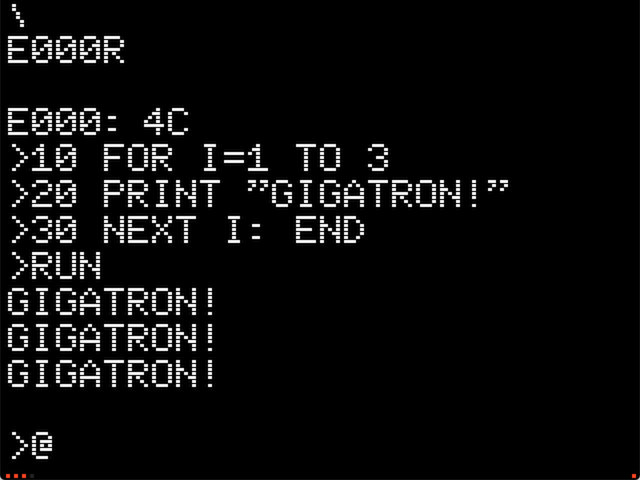
At67's compiler is the third BASIC for the Gigatron. The first was our port of Tiny BASIC more than a year ago. The second was MS BASIC with floating point. Today I decided that three BASICs aren't enough because we can have four.
We have Apple-1 emulation after all, so why not? Most work was to arrange the video table such that we have a 4K continuous block for Wozniak's original Apple-1 BASIC. We managed to free $6000-$6FFF in the 32K system. That mirrors to address $E000 and that is exactly where the original likes to sit. Then we reordered the zero page a bit and recompiled the A1 BASIC using cc65. Et voilà, there it runs!
![]()
-
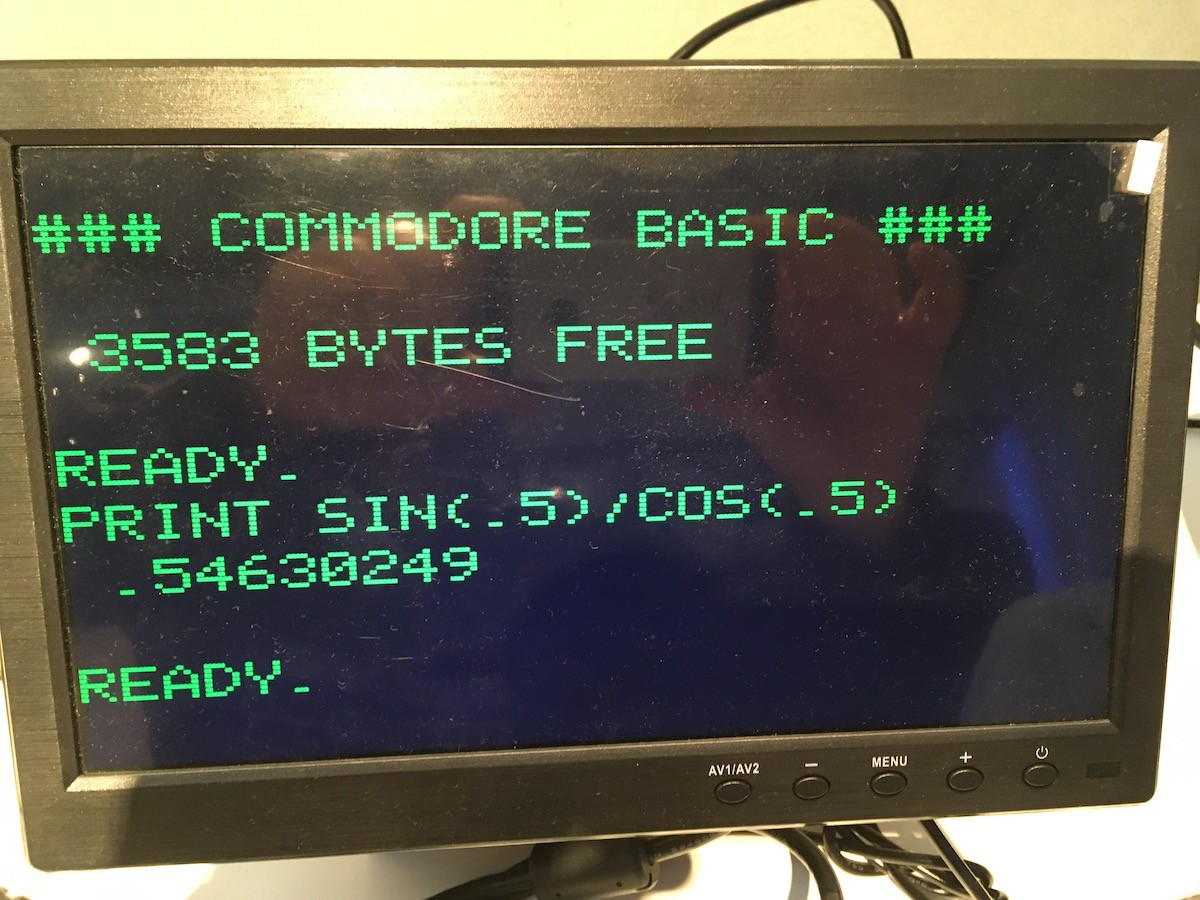
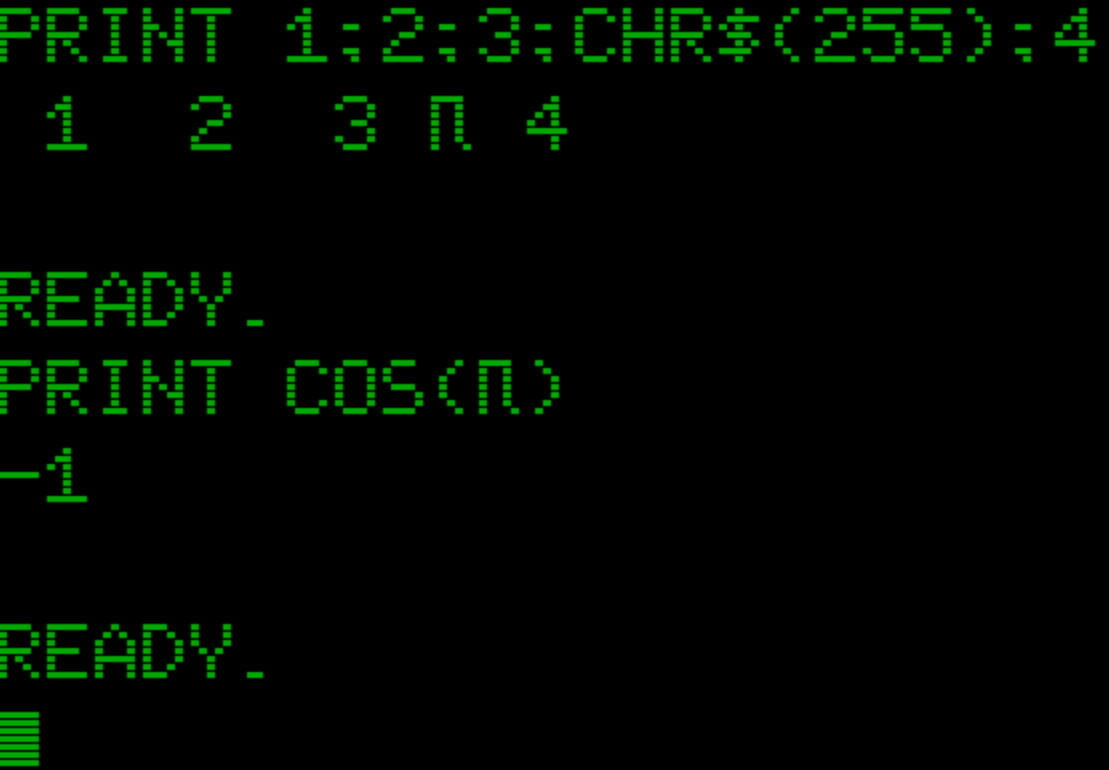
Micro-Soft BASIC and π
10/16/2019 at 19:32 • 0 commentsIt took a while, but now Micro-Soft BASIC is running on the 32K Gigatron! We already had Tiny BASIC of course, but that doesn't have 9 digits floating point (40 bits), let alone transcendental functions. Remember when Hackaday wrote that the Gigatron would probably never have floating point?
This is the BASIC that Paul Allen and Bill Gates wrote with Monte Davidoff and Ric Weiland, and for which they started Microsoft, or spelled Micro-Soft back then. They licensed it to many microcomputer builders, amongst others to Commodore. The version we have running is an early one for the Commodore PET.
Although the system can interpret 6502 code, there still was work to do: code, buffers, zero page variables and stack needed relocation, but that wasn't the biggest hurdle as Michael Steil's excellent set of reconstructed assembly sources made that relatively painless. The main problem was to create a sufficiently large continuous memory space. Although the Gigatron has 32K of RAM, 19KB of that is used for screen memory and the remainder is heavily fragmented. For example, by default the largest continuous block we have is just 512 bytes. BASIC itself needs 8KB, plus we need some K's for user program and variables. Ouch...
The first win is to disable the sound channels 2 through 4. That creates a continuous block from $200 to $800. For this trick you need ROM v4.
The next step is to compress the video memory. Our video resolution is already next to nothing, but we can always lower it even more! Of the 120 visible pixel lines, every 8th is always empty. At least, as long as we only use capitals, and for a mid-1970s BASIC that's perfectly acceptable. The empty pixel lines can then be shared for all rows of text. That saves 14*256 = 3585 bytes already.
The last trick is to increase the spacing between text lines from 1 to 4. This reduces the text lines from 15 to 11, but yields 4 * 7 * 256 =7,168 bytes.
Of course we then went overboard and added a flashing cursor, we made sure that the WAIT 6502 Easter Egg works, and that there is a π-symbol. The Gigatron doesn't have that in its font, but it does have T and U.... And... the font is stored without horizontal spacing, so there's our glyph:
R S T pi U | | | | | v v v v v x x x x . . x x x . x x # # # # . . . x x . . . x x . . . . . . # . . # . . . x x . . . x x . . . . . . # . . # . . . x x x x x . . x x x . . . # . . # . . . x x . x . . . . . . x . . # . . # . . . x x . . x . . . . . x . . # . . # . . . x x . . . x x x x x . . . # . . . # x x . . . . . . . . . . . . . . . . . . . . . 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 1 1 1 ^ 0 1 2 3 | font82up
Good enough for me:
![]()
-
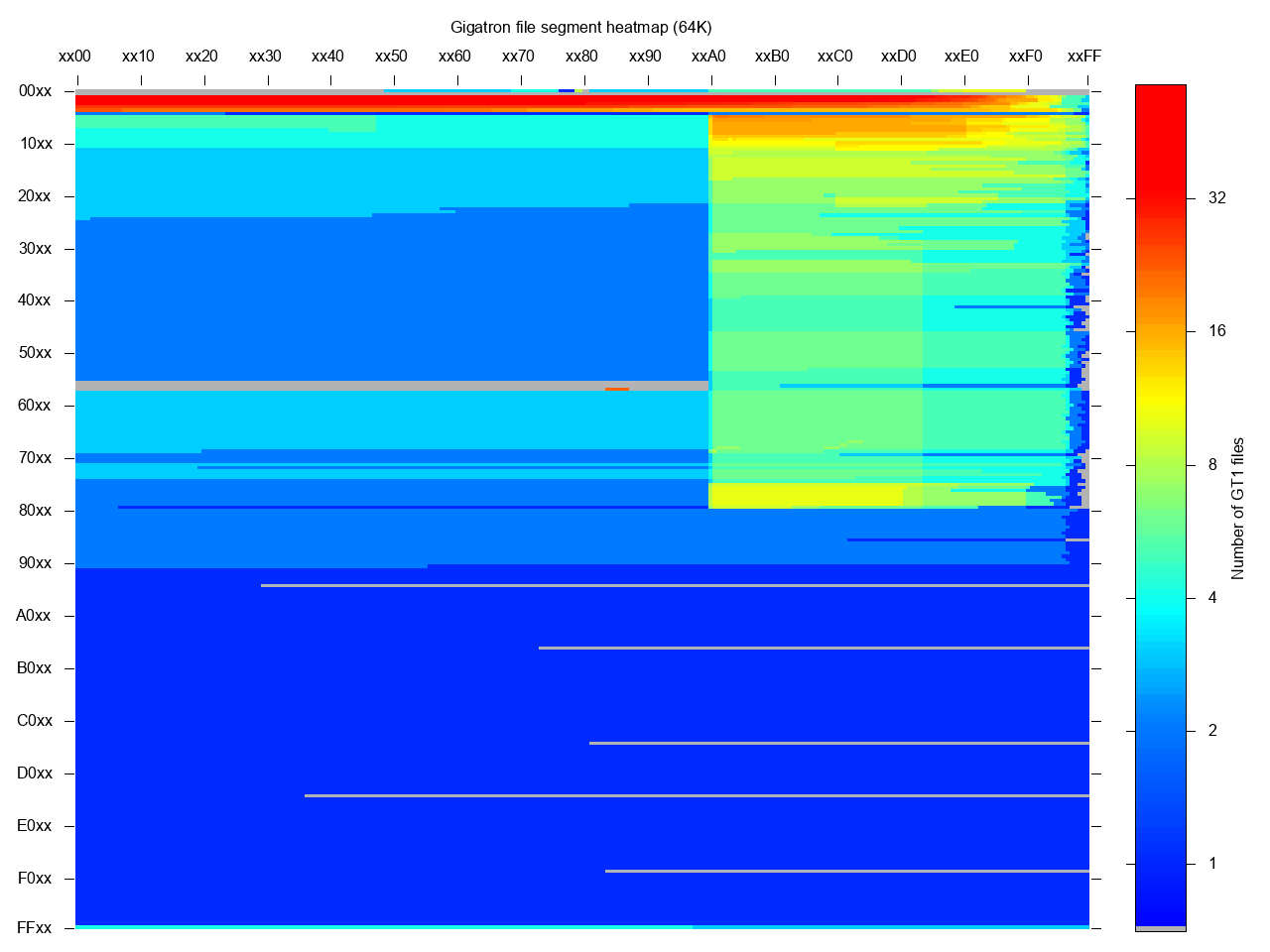
Heatmap of Gigatron applications
10/08/2019 at 16:01 • 0 commentsA static RAM map constructed by overlaying all GT1 files in the GitHub repo.
![]()
-
The anthem of 8-bit computing
08/13/2019 at 10:07 • 0 commentsA bunch of TTL chips playing the "anthem of 8-bit computing". Four channels: 2x pulse, 1x triangle, 1x noise
The player is an enhanced version of the Contrib/at67/midi player in the gigatron-rom repository. The noise is created from waveform 0 ("metallic") that receives a randomised XOR modulation 60 times per second.
Only 7400 logic. No microprocessor, no video chip, no sound chip.
![]()
The Arduino is used to load the music and player into RAM. You see that happen in the first few seconds of the video.
 Marcel van Kervinck
Marcel van Kervinck We have decided to stop selling kits once our stock has been sold, which should be in a few months. For us, the Gigatron was always about inventing new things, understanding technology, designing, fine tuning, tinkering, and also about meeting like minded people (and having fun in the process). Making it into a kit had its own charmes, writing a manual, sourcing components, designing a PCB. Packaging and sending out kits, however, resembles a plain job too much, but was needed to create a community of people that would also want to design, understand and tinker.
We have decided to stop selling kits once our stock has been sold, which should be in a few months. For us, the Gigatron was always about inventing new things, understanding technology, designing, fine tuning, tinkering, and also about meeting like minded people (and having fun in the process). Making it into a kit had its own charmes, writing a manual, sourcing components, designing a PCB. Packaging and sending out kits, however, resembles a plain job too much, but was needed to create a community of people that would also want to design, understand and tinker.