As mentioned in the last log, the DAC on the FL2K VGA chipset introduces a frequency roll-off due to the first-order hold. This roll-off is sinc-shaped, with the first zero at the sampling frequency. As a result, an output at the Nyquist frequency is down 3.92dB, while one at 50% of the Nyquist frequency is 0.91dB down.
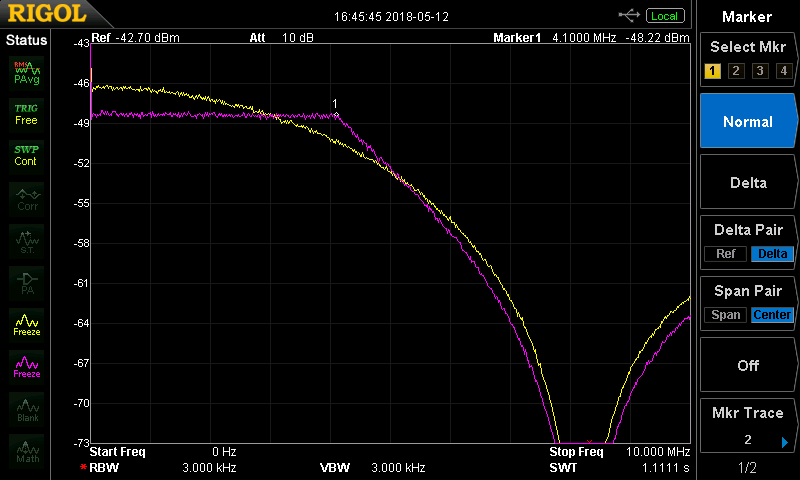
I wrote a little python code to implement a compensation filter for this issue. Using a filter like this, you can pre-equalize the signal to flatten the post-DAC frequency response. You can see the results in the above spectra. Both signals start as random samples from the python numpy.rand() function: their spectra should be flat. The yellow trace shows the signal sent directly to the DAC with the resulting frequency roll-off. For the magenta trace, the samples were first filtered with a 31-tap FIR filter designed to compensate for the rolloff. Note that the sampling frequency here is 8.192 MHz, putting the Nyquist frequency at 4.096MHz, very near the marker at 4.1MHz.
To generate the filter, I used the scipy.signal.firls() function to least-sqaures fit a filter to 1/sinc(f):
import numpy as np
from scipy import signal
N = 100
bands = np.linspace(0, 1, N)[1:-1]
bands = np.repeat(bands, 2)
bands = np.append(bands, 1)
bands = np.insert(bands, 0, 0)
desired = 1/np.sinc(bands/2)
b = signal.firls(31, bands, desired)
Most of the work is setting up the frequency bands. The desired response is the inverse of the sinc rolloff. The noise was generated with the np.random.rand() function, and the noise is compensated by filtering with the signal.lfilter() function:
n_samples = 8192 * 1000 * 20
noise = np.random.rand(n_samples)
comp_noise = signal.lfilter(b, 1, noise)
comp_noise *= 1./np.amax(np.abs(comp_noise))
Because the filter has a gain greater than one, I divide the result by the maximum signal level to keep the filtered signal within the DAC range.
There are several other ways to deal with this roll-off issue. Oversampling can reduce the impact because the sinc function is relatively flat near zero. The more you oversample, the less you'll notice the sinc rolloff. But, for signals using a significant portion of the available DAC bandwidth, this type of pre-compensation makes sense.
And of course, this issue doesn't only apply to noise, but to any signal generated with this DAC.
Measuring LPF Again
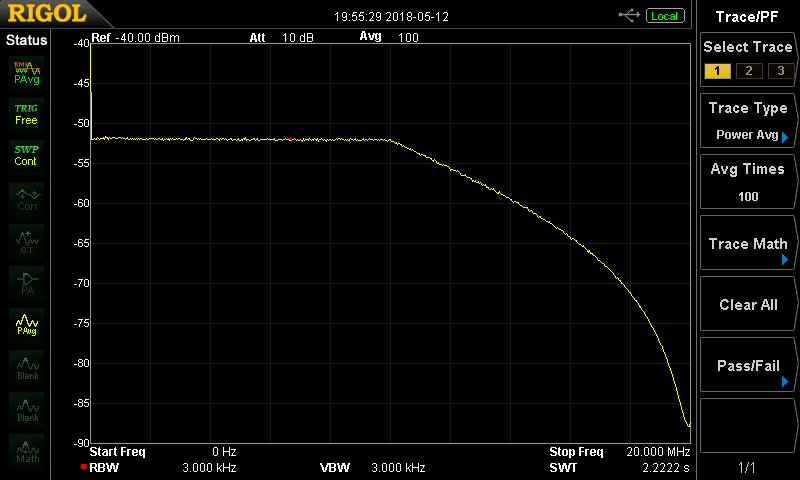
So, now that we have a flat noise spectrum, we can measure the LPF again, more confident that features in the stopband won't be hidden by the noise rolloff. In this case, I've used a 20MHz sample frequency, so the flat spectrum extends up to 10 MHz, as shown:
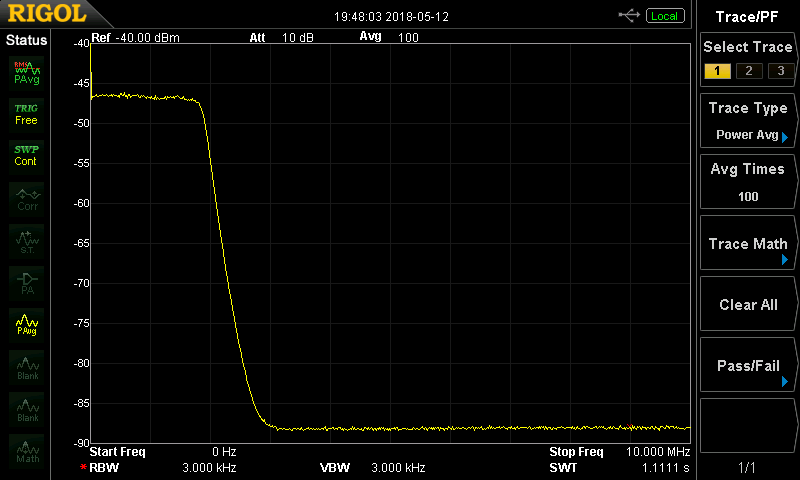
Inserting the LPF (now with the span set to 10 MHz), we have a better picture of the filter response:
 Ted Yapo
Ted Yapo
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.