"What is a computer, and what makes it different from all other man-made machines?"
Answering these questions leads to a surprisingly long cascade of concepts and practical decisions,. But interestingly, despite that computers are actually physical world implementations, they still keep a a very close relationship to pure concepts. Mathematics can be used to demonstrate the suitability of an abstract digital computer to solve any kind of problems using algorithms, and the Boolean algebra and its applied scientific counterpart, logic design, are the tools that helped transform these abstract machines into real ones.
Unlike abstract computers, real-world computers necessarily contain some limitations and rely on some physical architectures., Nevertheless, besides their differences, all these computer architectures still rely on the concept of processor, that executes instructions realizing logic and arithmetic operations.
Each project log will introduce another step towards the final goal of an optimized Arithmetic and Logic Unir (ALU) at the heart of the processor, made out of pure logic elements. This way, one can cherry pick a subject in particular, skip it if it is already mastered, or follow each step in turn to learn logic design with almost no prerequisite but common sense.
Beware! This project will go far beyond the classical ALU design covered in academic courses. If you ever followed one of these courses in logic design and felt yourself proud of having acquired this knowledge, but with a mixed feeling of underachievement, read on, this project is for you!
By starting from the historical and almost philosophical perspective of a computer, the goal of this project is to dive quickly into the subject of logic design, although a minimum of Boolean algebra theory will necessarily be covered. The idea is to get used to the basic rules required to use the small Boolean logic elements as building blocks into circuits that progressively realize more and more complex operations.
As one of the most complex operation, the basic arithmetic adder will be covered first, pointing out its inherent performance problem. But clever pure logic optimizations will be carried out in order to overcome this problem, and further optimizations will enable us to integrate into the adder all required logic operations at no performance cost, and eventually another last useful digital operation will be added to provide a complete, extremely optimized ALU design.
These logs will use as little theory as possible to keep them readable by everybody, and its is hoped to have them as interactive as possible based on the user comments.
Hopefully in the end, this project will result in a hardware proof of concept in the form of a real-world circuit made out of discrete logic chips on a breadboard.
 Squonk42
Squonk42

 Source: Karsten Sperling,
Source: Karsten Sperling,  Source: See page for author [Public domain],
Source: See page for author [Public domain],  Source: See page for author [Public domain],
Source: See page for author [Public domain], 


 Blair Vidakovich
Blair Vidakovich
 Julián Lell
Julián Lell
 Kara Abdelaziz
Kara Abdelaziz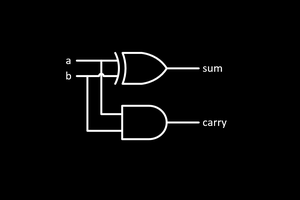
 Luke Valenty
Luke Valenty
TI's SN74CBT3251 or NXP's CBT3251. Same pinout as your 74151, but with real bi-diectional 5ohm switches. Ditch lookhead in favor of relay style instant pass-through. 6nS to set up switches, but propagate through all slices at 0.25nS therafter.
https://hackaday.io/project/174243/gallery#aa20bce890fa8bb9fb0c2dccb1f2d148
Not to worry. Last I checked, Dallas was still East of the Pecos. Can't rotate right, but can A+B, A-B, B-A in 16.25nS. Conditional logics and test for A=B, A<>B in 10.25nS. I figure a rotate afterward could set switches in parallel time. +.25nS to propagate the barrel, so was no point gumming up the ALU with it.