Inverse dynamics is a nonlinear control technique that provides a better trajectory tracking by calculating the required joint actuator torques that need to be generated by the motors to achieve a given trajectory.

The matrix form of the dynamics of a robot leg is given by Equation 44 where the and terms are neglected.

For a given and the non-linearity of the system can be vanished, making the system linear and hence the exact amount of torque that needs to be generated by the joint actuator to overcome the inertia of the actuator can be calculated. If the and match with the desired and then the projected trajectory will be tracked as expected [37].

Equation 45 shows the control law expression where is a new input to the system. The numeric value of is calculated by Equation 46 where is the desired trajectory, is the actual trajectory, and and are position and velocity gains, respectively [16].

Since the mass matrix, M, is invertible, equating Equation 45 to Equation 46 gives the expression in Equation 47 which shows that the new system is linear as it is given by Equation 48.

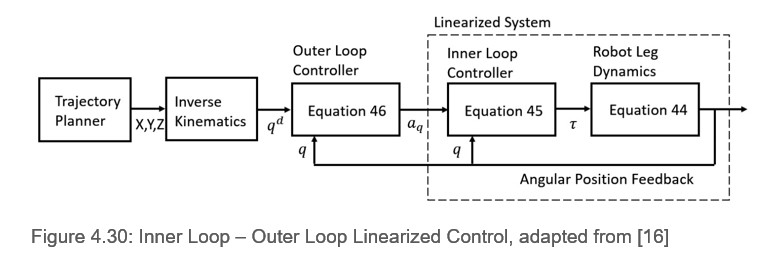
Figure 4.30 demonstrates the inner loop and outer loop control architecture where the output of the system yields the joint space signal which enables a better trajectory tracking given that the feedback gains and are tuned as appropriate.